
Question Number 177361 by jlewis last updated on 04/Oct/22
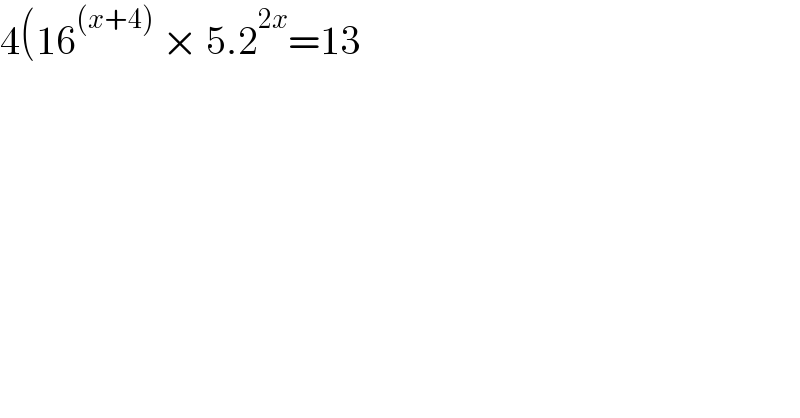
$$\mathrm{4}\left(\mathrm{16}^{\left({x}+\mathrm{4}\right)} \:×\:\mathrm{5}.\mathrm{2}^{\mathrm{2}{x}} =\mathrm{13}\right. \\ $$
Answered by a.lgnaoui last updated on 04/Oct/22
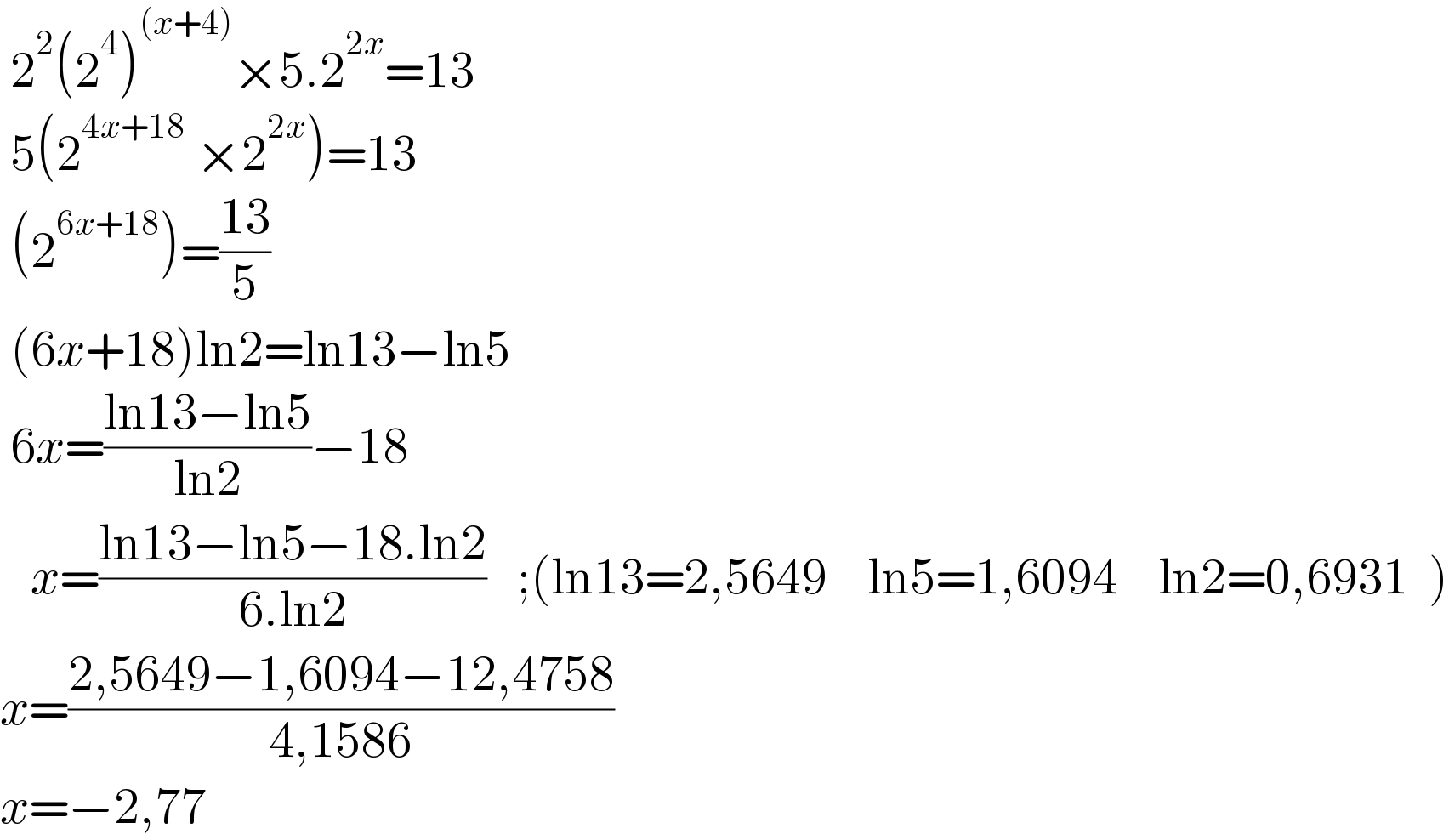
$$\:\mathrm{2}^{\mathrm{2}} \left(\mathrm{2}^{\mathrm{4}} \right)^{\left({x}+\mathrm{4}\right)} ×\mathrm{5}.\mathrm{2}^{\mathrm{2}{x}} =\mathrm{13} \\ $$$$\:\mathrm{5}\left(\mathrm{2}^{\mathrm{4}{x}+\mathrm{18}} \:×\mathrm{2}^{\mathrm{2}{x}} \right)=\mathrm{13} \\ $$$$\:\left(\mathrm{2}^{\mathrm{6}{x}+\mathrm{18}} \right)=\frac{\mathrm{13}}{\mathrm{5}}\:\:\: \\ $$$$\:\left(\mathrm{6}{x}+\mathrm{18}\right)\mathrm{ln2}=\mathrm{ln13}−\mathrm{ln5} \\ $$$$\:\mathrm{6}{x}=\frac{\mathrm{ln13}−\mathrm{ln5}}{\mathrm{ln2}}−\mathrm{18} \\ $$$$\:\:\:{x}=\frac{\mathrm{ln13}−\mathrm{ln5}−\mathrm{18}.\mathrm{ln2}}{\mathrm{6}.\mathrm{ln2}}\:\:\:;\left(\mathrm{ln13}=\mathrm{2},\mathrm{5649}\:\:\:\:\mathrm{ln5}=\mathrm{1},\mathrm{6094}\:\:\:\:\mathrm{ln2}=\mathrm{0},\mathrm{6931}\:\:\right) \\ $$$${x}=\frac{\mathrm{2},\mathrm{5649}−\mathrm{1},\mathrm{6094}−\mathrm{12},\mathrm{4758}}{\mathrm{4},\mathrm{1586}} \\ $$$${x}=−\mathrm{2},\mathrm{77} \\ $$
Commented by a.lgnaoui last updated on 04/Oct/22

$${excuse}\:{moi}\:{je}\:{ferai}\:{le}\:{necessaire}\:{pour}\: \\ $$$${minimiser}\:{le}\:{zoom}\:{sinon} \\ $$$$\left.{je}\:{prendrai}\:{l}\:{image}\:{d}'{ecran}\right) \\ $$$${thank}\:{you}. \\ $$
