Question and Answers Forum

All Questions      Topic List

Matrices and Determinants Questions

Previous in All Question      Next in All Question      

Previous in Matrices and Determinants      Next in Matrices and Determinants      

Question Number 6251 by net last updated on 20/Jun/16

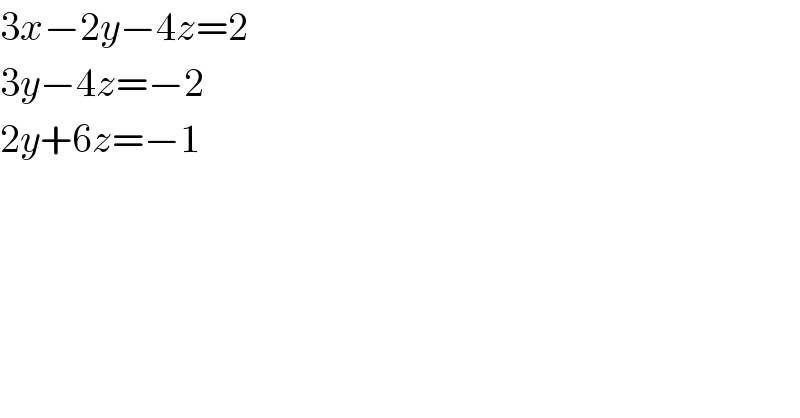
3x−2y−4z=2 3y−4z=−2 2y+6z=−1

$$\mathrm{3}{x}−\mathrm{2}{y}−\mathrm{4}{z}=\mathrm{2} \\ $$$$\mathrm{3}{y}−\mathrm{4}{z}=−\mathrm{2} \\ $$$$\mathrm{2}{y}+\mathrm{6}{z}=−\mathrm{1} \\ $$

Answered by Rasheed Soomro last updated on 20/Jun/16

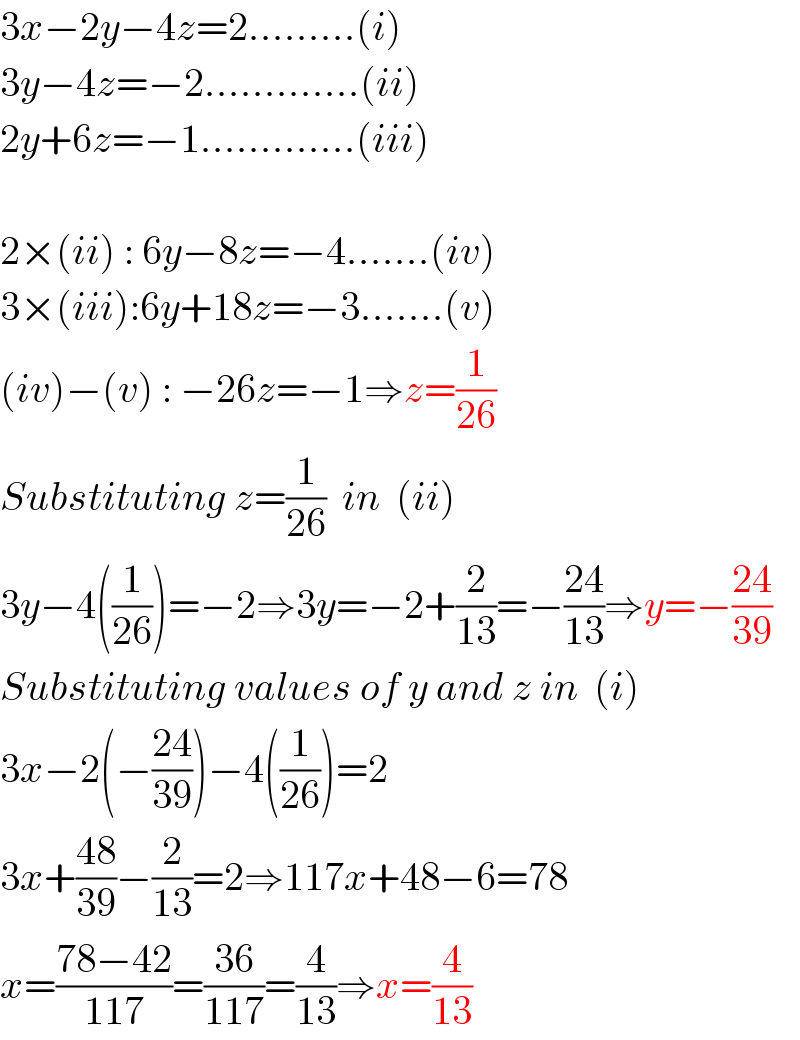
3x−2y−4z=2.........(i) 3y−4z=−2.............(ii) 2y+6z=−1.............(iii) 2×(ii) : 6y−8z=−4.......(iv) 3×(iii):6y+18z=−3.......(v) (iv)−(v) : −26z=−1⇒z=(1/(26)) Substituting z=(1/(26)) in (ii) 3y−4((1/(26)))=−2⇒3y=−2+(2/(13))=−((24)/(13))⇒y=−((24)/(39)) Substituting values of y and z in (i) 3x−2(−((24)/(39)))−4((1/(26)))=2 3x+((48)/(39))−(2/(13))=2⇒117x+48−6=78 x=((78−42)/(117))=((36)/(117))=(4/(13))⇒x=(4/(13))

$$\mathrm{3}{x}−\mathrm{2}{y}−\mathrm{4}{z}=\mathrm{2}.........\left({i}\right) \\ $$$$\mathrm{3}{y}−\mathrm{4}{z}=−\mathrm{2}.............\left({ii}\right) \\ $$$$\mathrm{2}{y}+\mathrm{6}{z}=−\mathrm{1}.............\left({iii}\right) \\ $$$$ \\ $$$$\mathrm{2}×\left({ii}\right)\::\:\mathrm{6}{y}−\mathrm{8}{z}=−\mathrm{4}.......\left({iv}\right) \\ $$$$\mathrm{3}×\left({iii}\right):\mathrm{6}{y}+\mathrm{18}{z}=−\mathrm{3}.......\left({v}\right) \\ $$$$\left({iv}\right)−\left({v}\right)\::\:−\mathrm{26}{z}=−\mathrm{1}\Rightarrow{z}=\frac{\mathrm{1}}{\mathrm{26}} \\ $$$${Substituting}\:{z}=\frac{\mathrm{1}}{\mathrm{26}}\:\:{in}\:\:\left({ii}\right) \\ $$$$\mathrm{3}{y}−\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{26}}\right)=−\mathrm{2}\Rightarrow\mathrm{3}{y}=−\mathrm{2}+\frac{\mathrm{2}}{\mathrm{13}}=−\frac{\mathrm{24}}{\mathrm{13}}\Rightarrow{y}=−\frac{\mathrm{24}}{\mathrm{39}} \\ $$$${Substituting}\:{values}\:{of}\:{y}\:{and}\:{z}\:{in}\:\:\left({i}\right) \\ $$$$\mathrm{3}{x}−\mathrm{2}\left(−\frac{\mathrm{24}}{\mathrm{39}}\right)−\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{26}}\right)=\mathrm{2} \\ $$$$\mathrm{3}{x}+\frac{\mathrm{48}}{\mathrm{39}}−\frac{\mathrm{2}}{\mathrm{13}}=\mathrm{2}\Rightarrow\mathrm{117}{x}+\mathrm{48}−\mathrm{6}=\mathrm{78} \\ $$$${x}=\frac{\mathrm{78}−\mathrm{42}}{\mathrm{117}}=\frac{\mathrm{36}}{\mathrm{117}}=\frac{\mathrm{4}}{\mathrm{13}}\Rightarrow{x}=\frac{\mathrm{4}}{\mathrm{13}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com