
Question Number 95495 by i jagooll last updated on 25/May/20
![3cos^2 x − 3cos x sin x + 2sin x = 1 x ∈ [ 0, 2π ]](Q95495.png)
$$\mathrm{3cos}\:^{\mathrm{2}} {x}\:−\:\mathrm{3cos}\:{x}\:\mathrm{sin}\:{x}\:+\:\mathrm{2sin}\:{x}\:=\:\mathrm{1} \\ $$$${x}\:\in\:\left[\:\mathrm{0},\:\mathrm{2}\pi\:\right]\: \\ $$
Answered by bobhans last updated on 25/May/20
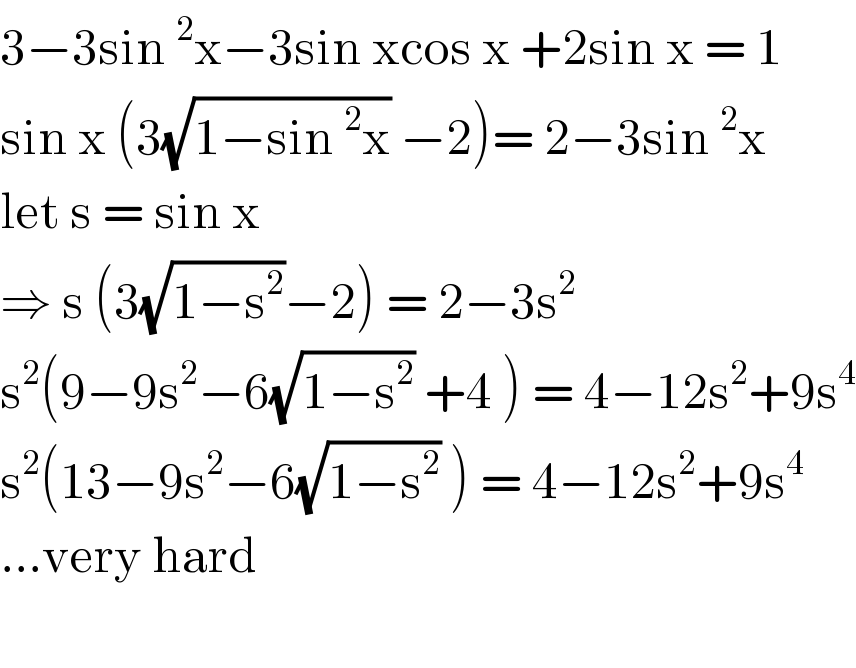
$$\mathrm{3}−\mathrm{3sin}\:^{\mathrm{2}} \mathrm{x}−\mathrm{3sin}\:\mathrm{xcos}\:\mathrm{x}\:+\mathrm{2sin}\:\mathrm{x}\:=\:\mathrm{1} \\ $$$$\mathrm{sin}\:\mathrm{x}\:\left(\mathrm{3}\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}\:−\mathrm{2}\right)=\:\mathrm{2}−\mathrm{3sin}\:^{\mathrm{2}} \mathrm{x}\: \\ $$$$\mathrm{let}\:\mathrm{s}\:=\:\mathrm{sin}\:\mathrm{x}\: \\ $$$$\Rightarrow\:\mathrm{s}\:\left(\mathrm{3}\sqrt{\mathrm{1}−\mathrm{s}^{\mathrm{2}} }−\mathrm{2}\right)\:=\:\mathrm{2}−\mathrm{3s}^{\mathrm{2}} \\ $$$$\mathrm{s}^{\mathrm{2}} \left(\mathrm{9}−\mathrm{9s}^{\mathrm{2}} −\mathrm{6}\sqrt{\mathrm{1}−\mathrm{s}^{\mathrm{2}} }\:+\mathrm{4}\:\right)\:=\:\mathrm{4}−\mathrm{12s}^{\mathrm{2}} +\mathrm{9s}^{\mathrm{4}} \\ $$$$\mathrm{s}^{\mathrm{2}} \left(\mathrm{13}−\mathrm{9s}^{\mathrm{2}} −\mathrm{6}\sqrt{\mathrm{1}−\mathrm{s}^{\mathrm{2}} }\:\right)\:=\:\mathrm{4}−\mathrm{12s}^{\mathrm{2}} +\mathrm{9s}^{\mathrm{4}} \\ $$$$...\mathrm{very}\:\mathrm{hard}\: \\ $$$$ \\ $$
Answered by john santu last updated on 25/May/20
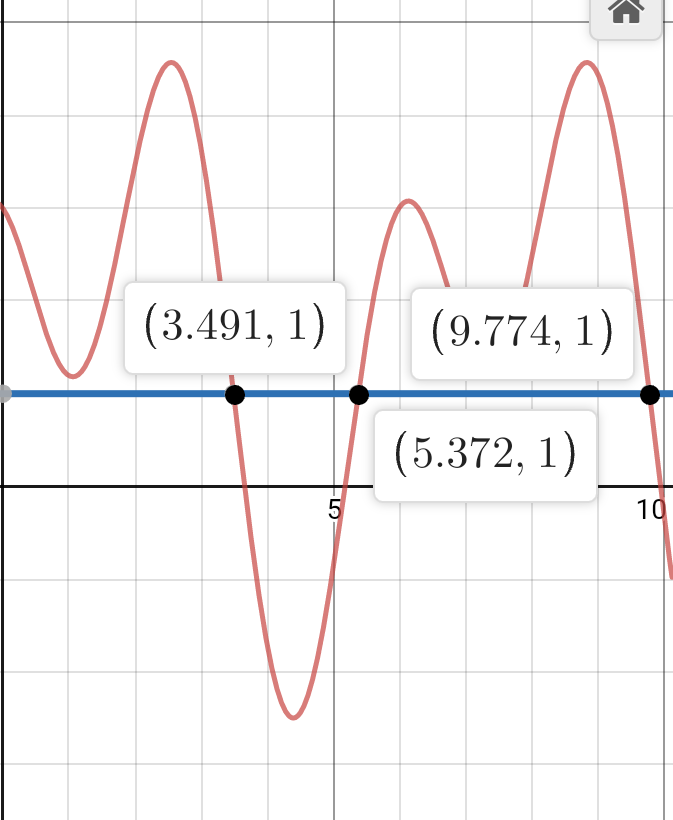
Commented by john santu last updated on 25/May/20

$$\mathrm{by}\:\mathrm{desmos}\: \\ $$
