Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 78762 by ajfour last updated on 20/Jan/20

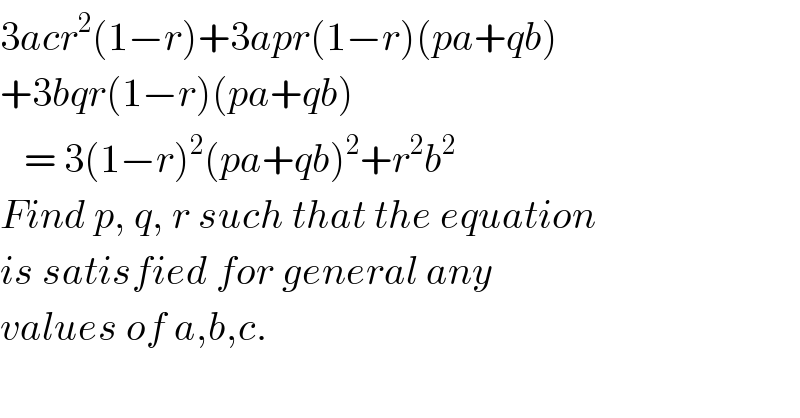
3acr^2 (1−r)+3apr(1−r)(pa+qb) +3bqr(1−r)(pa+qb) = 3(1−r)^2 (pa+qb)^2 +r^2 b^2 Find p, q, r such that the equation is satisfied for general any values of a,b,c.

$$\mathrm{3}{acr}^{\mathrm{2}} \left(\mathrm{1}−{r}\right)+\mathrm{3}{apr}\left(\mathrm{1}−{r}\right)\left({pa}+{qb}\right) \\ $$$$+\mathrm{3}{bqr}\left(\mathrm{1}−{r}\right)\left({pa}+{qb}\right) \\ $$$$\:\:\:=\:\mathrm{3}\left(\mathrm{1}−{r}\right)^{\mathrm{2}} \left({pa}+{qb}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$${Find}\:{p},\:{q},\:{r}\:{such}\:{that}\:{the}\:{equation} \\ $$$${is}\:{satisfied}\:{for}\:{general}\:{any} \\ $$$${values}\:{of}\:{a},{b},{c}.\: \\ $$

Commented by ajfour last updated on 20/Jan/20

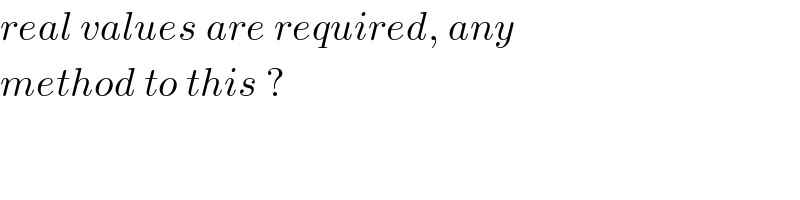
real values are required, any method to this ?

$${real}\:{values}\:{are}\:{required},\:{any} \\ $$$${method}\:{to}\:{this}\:? \\ $$

Answered by mr W last updated on 20/Jan/20

3r^2 (1−r)ac+3p^2 r(1−r)a^2 +6pqr(1−r)ab+3q^2 r(1−r)b^2 =3p^2 (1−r)^2 a^2 +[3q^2 (1−r)^2 −r^2 ]b^2 +6pq(1−r)^2 ab 3r^2 (1−r)=0 ⇒r=0 or 1 3p^2 r(1−r)=3p^2 (1−r)^2 ⇒r=0,p=0 or r=1,p=any 3q^2 r(1−r)=3q^2 (1−r)^2 −r^2 ⇒r=0,q=0 or r=1,q=impossible 6pqr(1−r)=6pq(1−r)^2 ⇒r=p=q=0 ⇒only possibility is p=q=r=0.

$$\mathrm{3}{r}^{\mathrm{2}} \left(\mathrm{1}−{r}\right){ac}+\mathrm{3}{p}^{\mathrm{2}} {r}\left(\mathrm{1}−{r}\right){a}^{\mathrm{2}} +\mathrm{6}{pqr}\left(\mathrm{1}−{r}\right){ab}+\mathrm{3}{q}^{\mathrm{2}} {r}\left(\mathrm{1}−{r}\right){b}^{\mathrm{2}} \\ $$$$=\mathrm{3}{p}^{\mathrm{2}} \left(\mathrm{1}−{r}\right)^{\mathrm{2}} {a}^{\mathrm{2}} +\left[\mathrm{3}{q}^{\mathrm{2}} \left(\mathrm{1}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} \right]{b}^{\mathrm{2}} +\mathrm{6}{pq}\left(\mathrm{1}−{r}\right)^{\mathrm{2}} {ab} \\ $$$$\mathrm{3}{r}^{\mathrm{2}} \left(\mathrm{1}−{r}\right)=\mathrm{0}\:\Rightarrow{r}=\mathrm{0}\:{or}\:\mathrm{1} \\ $$$$\mathrm{3}{p}^{\mathrm{2}} {r}\left(\mathrm{1}−{r}\right)=\mathrm{3}{p}^{\mathrm{2}} \left(\mathrm{1}−{r}\right)^{\mathrm{2}} \Rightarrow{r}=\mathrm{0},{p}=\mathrm{0}\:{or}\:{r}=\mathrm{1},{p}={any} \\ $$$$\mathrm{3}{q}^{\mathrm{2}} {r}\left(\mathrm{1}−{r}\right)=\mathrm{3}{q}^{\mathrm{2}} \left(\mathrm{1}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} \:\Rightarrow{r}=\mathrm{0},{q}=\mathrm{0}\:{or}\:{r}=\mathrm{1},{q}={impossible} \\ $$$$\mathrm{6}{pqr}\left(\mathrm{1}−{r}\right)=\mathrm{6}{pq}\left(\mathrm{1}−{r}\right)^{\mathrm{2}} \Rightarrow{r}={p}={q}=\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow{only}\:{possibility}\:{is}\:{p}={q}={r}=\mathrm{0}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com