Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 38114 by maxmathsup by imad last updated on 21/Jun/18

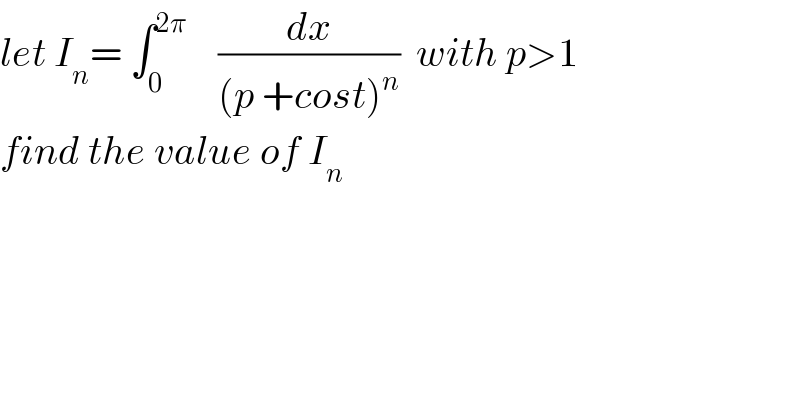
let I_n = ∫_0 ^(2π) (dx/((p +cost)^n )) with p>1 find the value of I_n

$${let}\:{I}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\frac{{dx}}{\left({p}\:+{cost}\right)^{{n}} }\:\:{with}\:{p}>\mathrm{1} \\ $$ $${find}\:{the}\:{value}\:{of}\:{I}_{{n}} \\ $$

Commented byabdo mathsup 649 cc last updated on 08/Jul/18

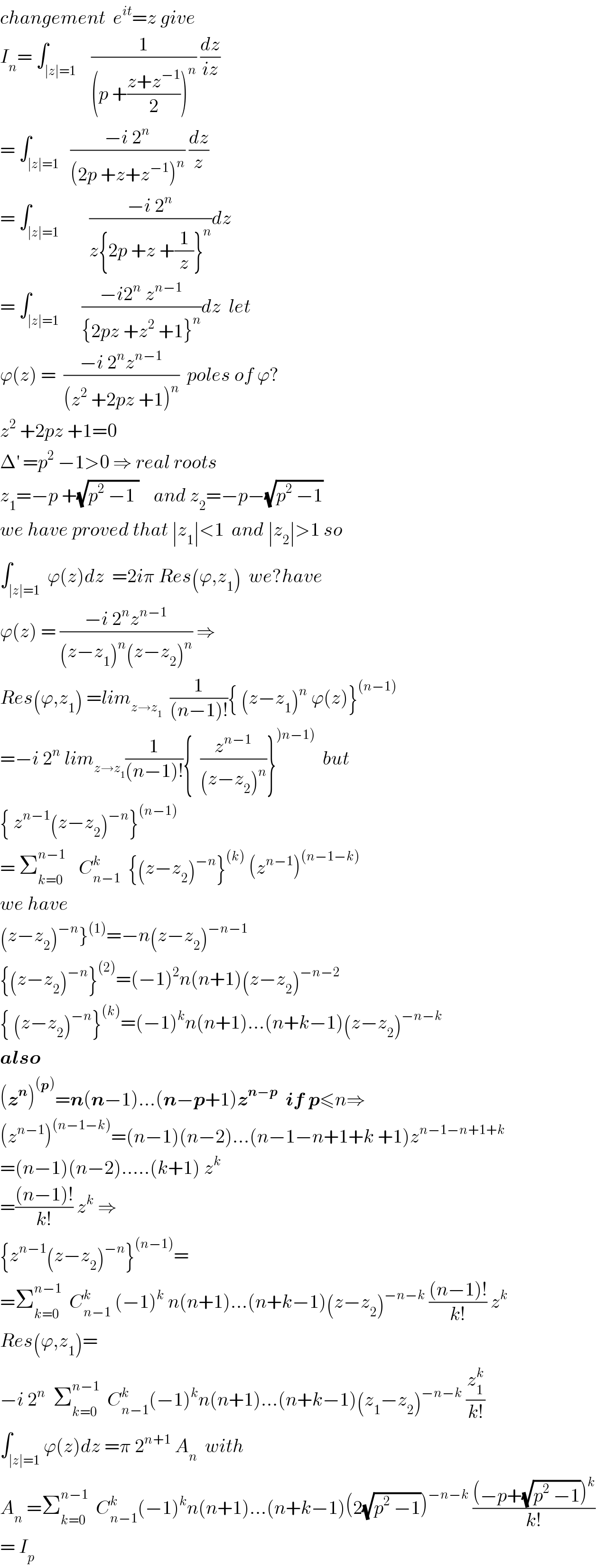
changement e^(it) =z give I_n = ∫_(∣z∣=1) (1/((p +((z+z^(−1) )/2))^n )) (dz/(iz)) = ∫_(∣z∣=1) ((−i 2^n )/((2p +z+z^(−1) )^n )) (dz/z) = ∫_(∣z∣=1) ((−i 2^n )/(z{2p +z +(1/z)}^n ))dz = ∫_(∣z∣=1) ((−i2^n z^(n−1) )/({2pz +z^2 +1}^n ))dz let ϕ(z) = ((−i 2^n z^(n−1) )/((z^2 +2pz +1)^n )) poles of ϕ? z^2 +2pz +1=0 Δ^′ =p^2 −1>0 ⇒ real roots z_1 =−p +(√(p^2 −1 )) and z_2 =−p−(√(p^2 −1)) we have proved that ∣z_1 ∣<1 and ∣z_2 ∣>1 so ∫_(∣z∣=1) ^ ϕ(z)dz =2iπ Res(ϕ,z_1 ) we?have ϕ(z) = ((−i 2^n z^(n−1) )/((z−z_1 )^n (z−z_2 )^n )) ⇒ Res(ϕ,z_1 ) =lim_(z→z_1 ) (1/((n−1)!)){ (z−z_1 )^n ϕ(z)}^((n−1)) =−i 2^n lim_(z→z_1 ) (1/((n−1)!)){ (z^(n−1) /((z−z_2 )^n ))}^()n−1)) but { z^(n−1) (z−z_2 )^(−n) }^((n−1)) = Σ_(k=0) ^(n−1 ) C_(n−1) ^(k ) {(z−z_2 )^(−n) }^((k)) (z^(n−1) )^((n−1−k)) we have (z−z_2 )^(−n) }^((1)) =−n(z−z_2 )^(−n−1) {(z−z_2 )^(−n) }^((2)) =(−1)^2 n(n+1)(z−z_2 )^(−n−2) { (z−z_2 )^(−n) }^((k)) =(−1)^k n(n+1)...(n+k−1)(z−z_2 )^(−n−k) also (z^n )^((p)) =n(n−1)...(n−p+1)z^(n−p) if p≤n⇒ (z^(n−1) )^((n−1−k)) =(n−1)(n−2)...(n−1−n+1+k +1)z^(n−1−n+1+k) =(n−1)(n−2).....(k+1) z^k =(((n−1)!)/(k!)) z^k ⇒ {z^(n−1) (z−z_2 )^(−n) }^((n−1)) = =Σ_(k=0) ^(n−1) C_(n−1) ^k (−1)^k n(n+1)...(n+k−1)(z−z_2 )^(−n−k) (((n−1)!)/(k!)) z^k Res(ϕ,z_1 )= −i 2^n Σ_(k=0) ^(n−1) C_(n−1) ^k (−1)^k n(n+1)...(n+k−1)(z_1 −z_2 )^(−n−k) (z_1 ^k /(k!)) ∫_(∣z∣=1) ϕ(z)dz =π 2^(n+1) A_n with A_n =Σ_(k=0) ^(n−1) C_(n−1) ^k (−1)^k n(n+1)...(n+k−1)(2(√(p^2 −1)))^(−n−k) (((−p+(√(p^2 −1)))^k )/(k!)) = I_p

$${changement}\:\:{e}^{{it}} ={z}\:{give}\: \\ $$ $${I}_{{n}} =\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{1}}{\left({p}\:+\frac{{z}+{z}^{−\mathrm{1}} }{\mathrm{2}}\right)^{{n}} }\:\frac{{dz}}{{iz}} \\ $$ $$=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\frac{−{i}\:\mathrm{2}^{{n}} }{\left(\mathrm{2}{p}\:+{z}+{z}^{−\mathrm{1}} \right)^{{n}} }\:\frac{{dz}}{{z}} \\ $$ $$=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\:\:\frac{−{i}\:\mathrm{2}^{{n}} }{{z}\left\{\mathrm{2}{p}\:+{z}\:+\frac{\mathrm{1}}{{z}}\right\}^{{n}} }{dz} \\ $$ $$=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\frac{−{i}\mathrm{2}^{{n}} \:{z}^{{n}−\mathrm{1}} }{\left\{\mathrm{2}{pz}\:+{z}^{\mathrm{2}} \:+\mathrm{1}\right\}^{{n}} }{dz}\:\:{let} \\ $$ $$\varphi\left({z}\right)\:=\:\:\frac{−{i}\:\mathrm{2}^{{n}} {z}^{{n}−\mathrm{1}} }{\left({z}^{\mathrm{2}} \:+\mathrm{2}{pz}\:+\mathrm{1}\right)^{{n}} }\:\:{poles}\:{of}\:\varphi? \\ $$ $${z}^{\mathrm{2}} \:+\mathrm{2}{pz}\:+\mathrm{1}=\mathrm{0} \\ $$ $$\Delta^{'} \:={p}^{\mathrm{2}} \:−\mathrm{1}>\mathrm{0}\:\Rightarrow\:{real}\:{roots} \\ $$ $${z}_{\mathrm{1}} =−{p}\:+\sqrt{{p}^{\mathrm{2}} \:−\mathrm{1}\:}\:\:\:\:{and}\:{z}_{\mathrm{2}} =−{p}−\sqrt{{p}^{\mathrm{2}} \:−\mathrm{1}} \\ $$ $${we}\:{have}\:{proved}\:{that}\:\mid{z}_{\mathrm{1}} \mid<\mathrm{1}\:\:{and}\:\mid{z}_{\mathrm{2}} \mid>\mathrm{1}\:{so} \\ $$ $$\int_{\mid{z}\mid=\mathrm{1}} ^{} \:\varphi\left({z}\right){dz}\:\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{z}_{\mathrm{1}} \right)\:\:{we}?{have} \\ $$ $$\varphi\left({z}\right)\:=\:\frac{−{i}\:\mathrm{2}^{{n}} {z}^{{n}−\mathrm{1}} }{\left({z}−{z}_{\mathrm{1}} \right)^{{n}} \left({z}−{z}_{\mathrm{2}} \right)^{{n}} }\:\Rightarrow \\ $$ $${Res}\left(\varphi,{z}_{\mathrm{1}} \right)\:={lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \:\:\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}\left\{\:\left({z}−{z}_{\mathrm{1}} \right)^{{n}} \:\varphi\left({z}\right)\right\}^{\left({n}−\mathrm{1}\right)} \\ $$ $$=−{i}\:\mathrm{2}^{{n}} \:{lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}\left\{\:\:\frac{{z}^{{n}−\mathrm{1}} }{\left({z}−{z}_{\mathrm{2}} \right)^{{n}} }\right\}^{\left.\right)\left.{n}−\mathrm{1}\right)} \:\:{but} \\ $$ $$\left\{\:{z}^{{n}−\mathrm{1}} \left({z}−{z}_{\mathrm{2}} \right)^{−{n}} \right\}^{\left({n}−\mathrm{1}\right)} \\ $$ $$=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}\:} \:\:\:{C}_{{n}−\mathrm{1}} ^{{k}\:} \:\:\left\{\left({z}−{z}_{\mathrm{2}} \right)^{−{n}} \right\}^{\left({k}\right)} \:\left({z}^{{n}−\mathrm{1}} \right)^{\left({n}−\mathrm{1}−{k}\right)} \\ $$ $${we}\:{have} \\ $$ $$\left.\left({z}−{z}_{\mathrm{2}} \right)^{−{n}} \right\}^{\left(\mathrm{1}\right)} =−{n}\left({z}−{z}_{\mathrm{2}} \right)^{−{n}−\mathrm{1}} \\ $$ $$\left\{\left({z}−{z}_{\mathrm{2}} \right)^{−{n}} \right\}^{\left(\mathrm{2}\right)} =\left(−\mathrm{1}\right)^{\mathrm{2}} {n}\left({n}+\mathrm{1}\right)\left({z}−{z}_{\mathrm{2}} \right)^{−{n}−\mathrm{2}} \\ $$ $$\left\{\:\left({z}−{z}_{\mathrm{2}} \right)^{−{n}} \right\}^{\left({k}\right)} =\left(−\mathrm{1}\right)^{{k}} {n}\left({n}+\mathrm{1}\right)...\left({n}+{k}−\mathrm{1}\right)\left({z}−{z}_{\mathrm{2}} \right)^{−{n}−{k}} \\ $$ $$\boldsymbol{{also}} \\ $$ $$\left(\boldsymbol{{z}}^{\boldsymbol{{n}}} \right)^{\left(\boldsymbol{{p}}\right)} =\boldsymbol{{n}}\left(\boldsymbol{{n}}−\mathrm{1}\right)...\left(\boldsymbol{{n}}−\boldsymbol{{p}}+\mathrm{1}\right)\boldsymbol{{z}}^{\boldsymbol{{n}}−\boldsymbol{{p}}} \:\:\boldsymbol{{if}}\:\boldsymbol{{p}}\leqslant{n}\Rightarrow \\ $$ $$\left({z}^{{n}−\mathrm{1}} \right)^{\left({n}−\mathrm{1}−{k}\right)} =\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)...\left({n}−\mathrm{1}−{n}+\mathrm{1}+{k}\:+\mathrm{1}\right){z}^{{n}−\mathrm{1}−{n}+\mathrm{1}+{k}} \\ $$ $$=\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right).....\left({k}+\mathrm{1}\right)\:{z}^{{k}} \\ $$ $$=\frac{\left({n}−\mathrm{1}\right)!}{{k}!}\:{z}^{{k}} \:\Rightarrow \\ $$ $$\left\{{z}^{{n}−\mathrm{1}} \left({z}−{z}_{\mathrm{2}} \right)^{−{n}} \right\}^{\left({n}−\mathrm{1}\right)} = \\ $$ $$=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:{C}_{{n}−\mathrm{1}} ^{{k}} \:\left(−\mathrm{1}\right)^{{k}} \:{n}\left({n}+\mathrm{1}\right)...\left({n}+{k}−\mathrm{1}\right)\left({z}−{z}_{\mathrm{2}} \right)^{−{n}−{k}} \:\frac{\left({n}−\mathrm{1}\right)!}{{k}!}\:{z}^{{k}} \\ $$ $${Res}\left(\varphi,{z}_{\mathrm{1}} \right)= \\ $$ $$−{i}\:\mathrm{2}^{{n}} \:\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:{C}_{{n}−\mathrm{1}} ^{{k}} \left(−\mathrm{1}\right)^{{k}} {n}\left({n}+\mathrm{1}\right)...\left({n}+{k}−\mathrm{1}\right)\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)^{−{n}−{k}} \:\frac{{z}_{\mathrm{1}} ^{{k}} }{{k}!} \\ $$ $$\int_{\mid{z}\mid=\mathrm{1}} \varphi\left({z}\right){dz}\:=\pi\:\mathrm{2}^{{n}+\mathrm{1}} \:{A}_{{n}} \:\:{with} \\ $$ $${A}_{{n}} \:=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:{C}_{{n}−\mathrm{1}} ^{{k}} \left(−\mathrm{1}\right)^{{k}} {n}\left({n}+\mathrm{1}\right)...\left({n}+{k}−\mathrm{1}\right)\left(\mathrm{2}\sqrt{{p}^{\mathrm{2}} \:−\mathrm{1}}\right)^{−{n}−{k}} \:\frac{\left(−{p}+\sqrt{{p}^{\mathrm{2}} \:−\mathrm{1}}\right)^{{k}} }{{k}!} \\ $$ $$=\:{I}_{{p}} \\ $$

Commented byabdo mathsup 649 cc last updated on 08/Jul/18

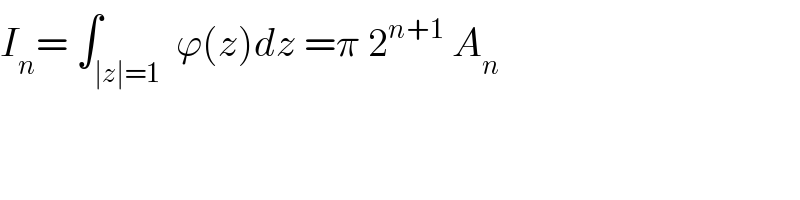
I_n = ∫_(∣z∣=1) ϕ(z)dz =π 2^(n+1) A_n

$${I}_{{n}} =\:\int_{\mid{z}\mid=\mathrm{1}} \:\varphi\left({z}\right){dz}\:=\pi\:\mathrm{2}^{{n}+\mathrm{1}} \:{A}_{{n}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com