
Question Number 38113 by maxmathsup by imad last updated on 21/Jun/18
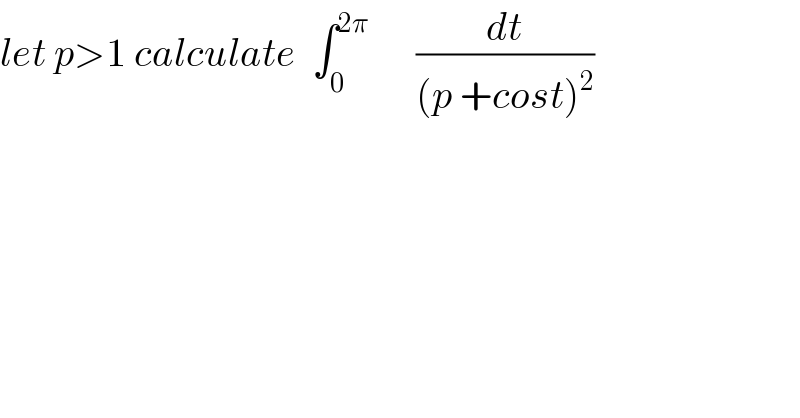
$${let}\:{p}>\mathrm{1}\:{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\:\:\frac{{dt}}{\left({p}\:+{cost}\right)^{\mathrm{2}} } \\ $$
Commented bymath khazana by abdo last updated on 08/Jul/18
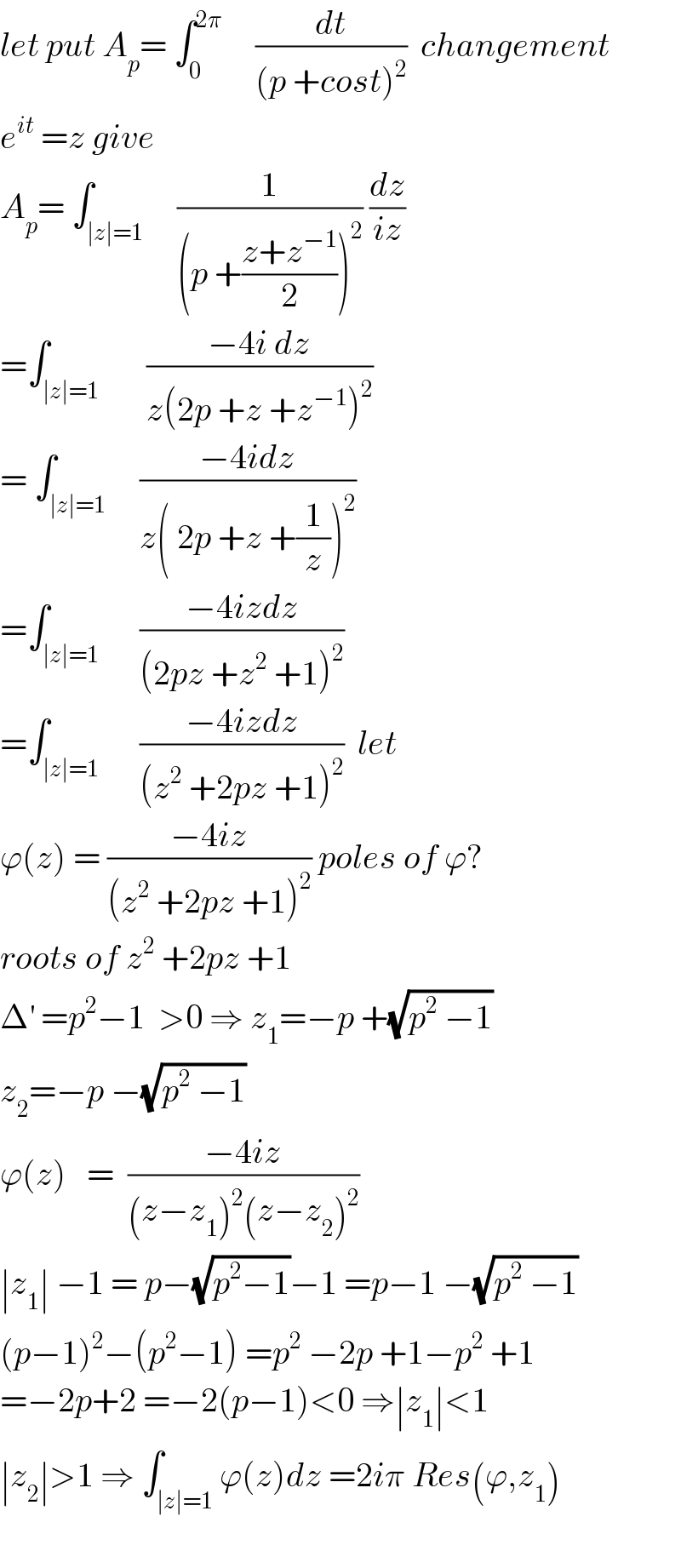
$${let}\:{put}\:{A}_{{p}} =\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\:\frac{{dt}}{\left({p}\:+{cost}\right)^{\mathrm{2}} }\:\:{changement} \\ $$ $${e}^{{it}} \:={z}\:{give} \\ $$ $${A}_{{p}} =\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{1}}{\left({p}\:+\frac{{z}+{z}^{−\mathrm{1}} }{\mathrm{2}}\right)^{\mathrm{2}} }\:\frac{{dz}}{{iz}} \\ $$ $$=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\:\frac{−\mathrm{4}{i}\:{dz}}{{z}\left(\mathrm{2}{p}\:+{z}\:+{z}^{−\mathrm{1}} \right)^{\mathrm{2}} } \\ $$ $$=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{−\mathrm{4}{idz}}{{z}\left(\:\mathrm{2}{p}\:+{z}\:+\frac{\mathrm{1}}{{z}}\right)^{\mathrm{2}} } \\ $$ $$=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\frac{−\mathrm{4}{izdz}}{\left(\mathrm{2}{pz}\:+{z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$ $$=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\frac{−\mathrm{4}{izdz}}{\left({z}^{\mathrm{2}} \:+\mathrm{2}{pz}\:+\mathrm{1}\right)^{\mathrm{2}} }\:\:{let} \\ $$ $$\varphi\left({z}\right)\:=\:\frac{−\mathrm{4}{iz}}{\left({z}^{\mathrm{2}} \:+\mathrm{2}{pz}\:+\mathrm{1}\right)^{\mathrm{2}} }\:{poles}\:{of}\:\varphi? \\ $$ $${roots}\:{of}\:{z}^{\mathrm{2}} \:+\mathrm{2}{pz}\:+\mathrm{1} \\ $$ $$\Delta^{'} \:={p}^{\mathrm{2}} −\mathrm{1}\:\:>\mathrm{0}\:\Rightarrow\:{z}_{\mathrm{1}} =−{p}\:+\sqrt{{p}^{\mathrm{2}} \:−\mathrm{1}} \\ $$ $${z}_{\mathrm{2}} =−{p}\:−\sqrt{{p}^{\mathrm{2}} \:−\mathrm{1}} \\ $$ $$\varphi\left({z}\right)\:\:\:=\:\:\frac{−\mathrm{4}{iz}}{\left({z}−{z}_{\mathrm{1}} \right)^{\mathrm{2}} \left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$ $$\mid{z}_{\mathrm{1}} \mid\:−\mathrm{1}\:=\:{p}−\sqrt{{p}^{\mathrm{2}} −\mathrm{1}}−\mathrm{1}\:={p}−\mathrm{1}\:−\sqrt{{p}^{\mathrm{2}} \:−\mathrm{1}} \\ $$ $$\left({p}−\mathrm{1}\right)^{\mathrm{2}} −\left({p}^{\mathrm{2}} −\mathrm{1}\right)\:={p}^{\mathrm{2}} \:−\mathrm{2}{p}\:+\mathrm{1}−{p}^{\mathrm{2}} \:+\mathrm{1} \\ $$ $$=−\mathrm{2}{p}+\mathrm{2}\:=−\mathrm{2}\left({p}−\mathrm{1}\right)<\mathrm{0}\:\Rightarrow\mid{z}_{\mathrm{1}} \mid<\mathrm{1} \\ $$ $$\mid{z}_{\mathrm{2}} \mid>\mathrm{1}\:\Rightarrow\:\int_{\mid{z}\mid=\mathrm{1}} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{z}_{\mathrm{1}} \right) \\ $$ $$ \\ $$
Commented bymath khazana by abdo last updated on 08/Jul/18
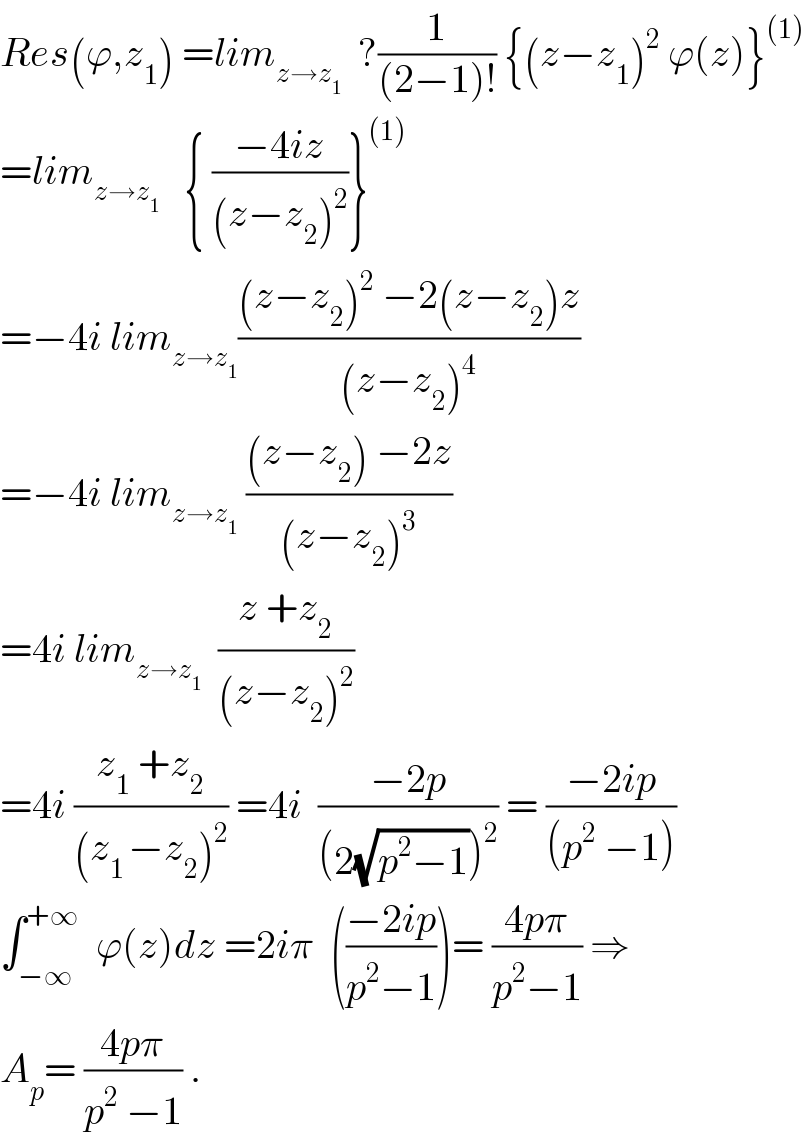
$${Res}\left(\varphi,{z}_{\mathrm{1}} \right)\:={lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \:\:?\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\:\left\{\left({z}−{z}_{\mathrm{1}} \right)^{\mathrm{2}} \:\varphi\left({z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$ $$={lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \:\:\:\left\{\:\frac{−\mathrm{4}{iz}}{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$ $$=−\mathrm{4}{i}\:{lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \frac{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{2}} \:−\mathrm{2}\left({z}−{z}_{\mathrm{2}} \right){z}}{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{4}} } \\ $$ $$=−\mathrm{4}{i}\:{lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \:\frac{\left({z}−{z}_{\mathrm{2}} \right)\:−\mathrm{2}{z}}{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$ $$=\mathrm{4}{i}\:{lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \:\:\frac{{z}\:+{z}_{\mathrm{2}} }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$ $$=\mathrm{4}{i}\:\frac{{z}_{\mathrm{1}} \:+{z}_{\mathrm{2}} }{\left({z}_{\mathrm{1}\:} −{z}_{\mathrm{2}} \right)^{\mathrm{2}} }\:=\mathrm{4}{i}\:\:\frac{−\mathrm{2}{p}}{\left(\mathrm{2}\sqrt{{p}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} }\:=\:\frac{−\mathrm{2}{ip}}{\left({p}^{\mathrm{2}} \:−\mathrm{1}\right)} \\ $$ $$\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\:\left(\frac{−\mathrm{2}{ip}}{{p}^{\mathrm{2}} −\mathrm{1}}\right)=\:\frac{\mathrm{4}{p}\pi}{{p}^{\mathrm{2}} −\mathrm{1}}\:\Rightarrow \\ $$ $${A}_{{p}} =\:\frac{\mathrm{4}{p}\pi}{{p}^{\mathrm{2}} \:−\mathrm{1}}\:. \\ $$
