
Question Number 37964 by naka3546 last updated on 20/Jun/18
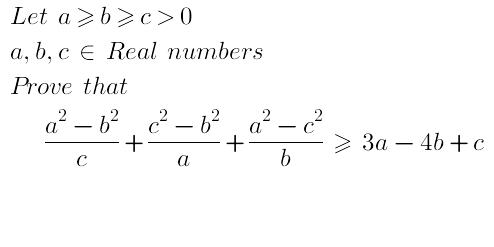
Answered by gunawan last updated on 20/Jun/18
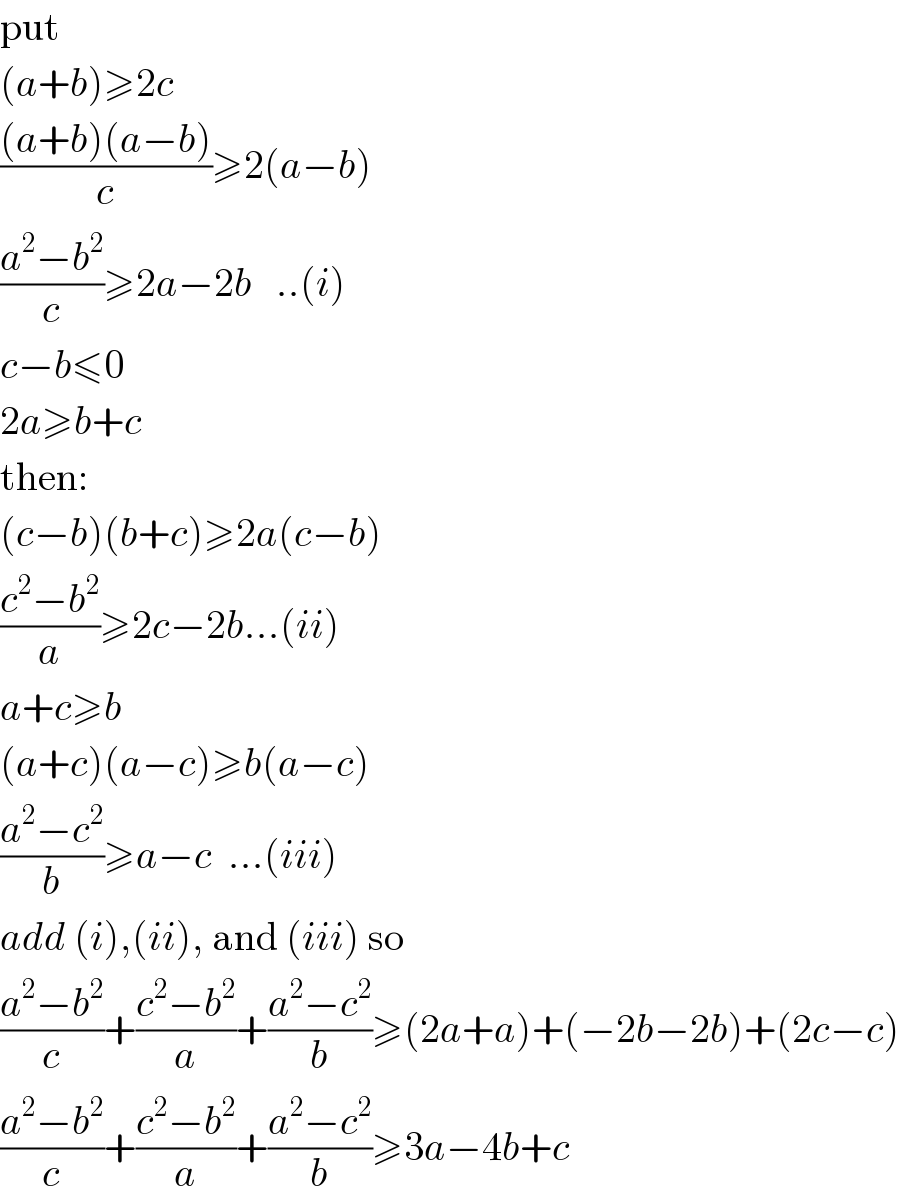
$$\mathrm{put}\: \\ $$$$\left({a}+{b}\right)\geqslant\mathrm{2}{c} \\ $$$$\frac{\left({a}+{b}\right)\left({a}−{b}\right)}{{c}}\geqslant\mathrm{2}\left({a}−{b}\right) \\ $$$$\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{c}}\geqslant\mathrm{2}{a}−\mathrm{2}{b}\:\:\:..\left({i}\right) \\ $$$${c}−{b}\leqslant\mathrm{0} \\ $$$$\mathrm{2}{a}\geqslant{b}+{c}\: \\ $$$$\mathrm{then}: \\ $$$$\left({c}−{b}\right)\left({b}+{c}\right)\geqslant\mathrm{2}{a}\left({c}−{b}\right) \\ $$$$\frac{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}}\geqslant\mathrm{2}{c}−\mathrm{2}{b}...\left({ii}\right) \\ $$$${a}+{c}\geqslant{b} \\ $$$$\left({a}+{c}\right)\left({a}−{c}\right)\geqslant{b}\left({a}−{c}\right) \\ $$$$\frac{{a}^{\mathrm{2}} −{c}^{\mathrm{2}} }{{b}}\geqslant{a}−{c}\:\:...\left({iii}\right) \\ $$$${add}\:\left({i}\right),\left({ii}\right),\:\mathrm{and}\:\left({iii}\right)\:\mathrm{so} \\ $$$$\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{c}}+\frac{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}}+\frac{{a}^{\mathrm{2}} −{c}^{\mathrm{2}} }{{b}}\geqslant\left(\mathrm{2}{a}+{a}\right)+\left(−\mathrm{2}{b}−\mathrm{2}{b}\right)+\left(\mathrm{2}{c}−{c}\right) \\ $$$$\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{c}}+\frac{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}}+\frac{{a}^{\mathrm{2}} −{c}^{\mathrm{2}} }{{b}}\geqslant\mathrm{3}{a}−\mathrm{4}{b}+{c} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 20/Jun/18

$${excellent}... \\ $$
