
Question Number 37871 by kunal1234523 last updated on 18/Jun/18

$$\mathrm{A}\:\mathrm{regular}\:\mathrm{pyramid}\:\mathrm{has}\:\mathrm{for}\:\mathrm{its}\:\mathrm{base}\:\mathrm{polygon} \\ $$$$\mathrm{of}\:{n}\:\mathrm{sides},\:\mathrm{and}\:\mathrm{each}\:\mathrm{slant}\:\mathrm{face}\:\mathrm{consist}\:\mathrm{of}\:\mathrm{an}\: \\ $$$$\mathrm{isosceles}\:\mathrm{triangle}\:\mathrm{of}\:\mathrm{vertical}\:\mathrm{angle}\:\mathrm{2}\alpha.\:\mathrm{If}\:\mathrm{the} \\ $$$$\mathrm{slant}\:\mathrm{faces}\:\mathrm{are}\:\mathrm{each}\:\mathrm{inclined}\:\mathrm{at}\:\mathrm{angle}\:\beta\:\mathrm{to}\: \\ $$$$\mathrm{the}\:\mathrm{base}\:,\:\mathrm{and}\:\mathrm{at}\:\mathrm{an}\:\mathrm{angle}\:\mathrm{2}\gamma\:\mathrm{to}\:\mathrm{one}\:\mathrm{another} \\ $$$$\mathrm{show}\:\mathrm{that} \\ $$$$\mathrm{cos}\beta\:=\:\mathrm{tan}\:\alpha\:\mathrm{cot}\frac{\pi}{\mathrm{n}}\:,\:\mathrm{and}\:\mathrm{sin}\gamma\:=\:\mathrm{sec}\:\alpha\:\mathrm{cos}\frac{\pi}{\mathrm{n}} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 18/Jun/18
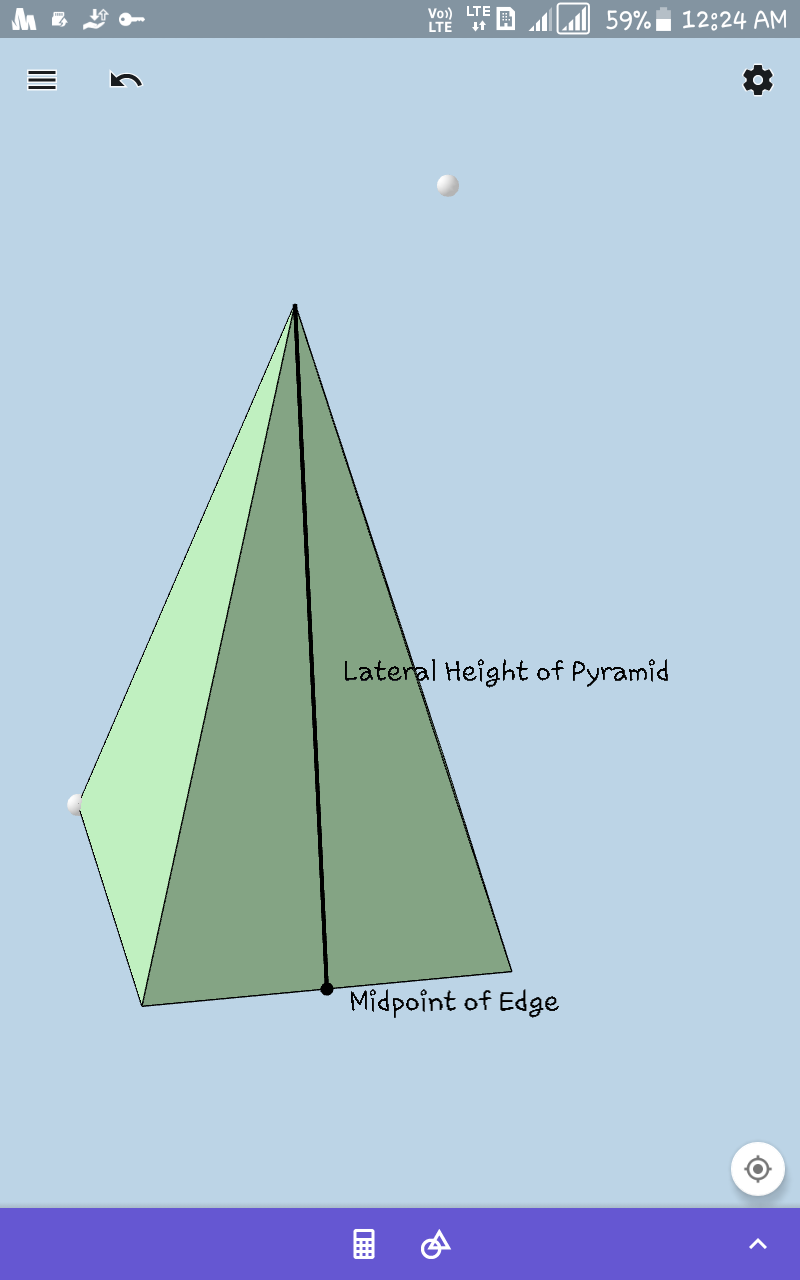
Commented by ajfour last updated on 18/Jun/18
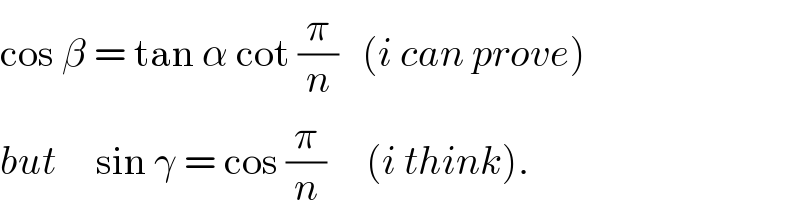
$$\mathrm{cos}\:\beta\:=\:\mathrm{tan}\:\alpha\:\mathrm{cot}\:\frac{\pi}{{n}}\:\:\:\left({i}\:{can}\:{prove}\right) \\ $$$${but}\:\:\:\:\:\mathrm{sin}\:\gamma\:=\:\mathrm{cos}\:\frac{\pi}{{n}}\:\:\:\:\:\left({i}\:{think}\right). \\ $$
