
Question Number 37745 by kunal1234523 last updated on 17/Jun/18
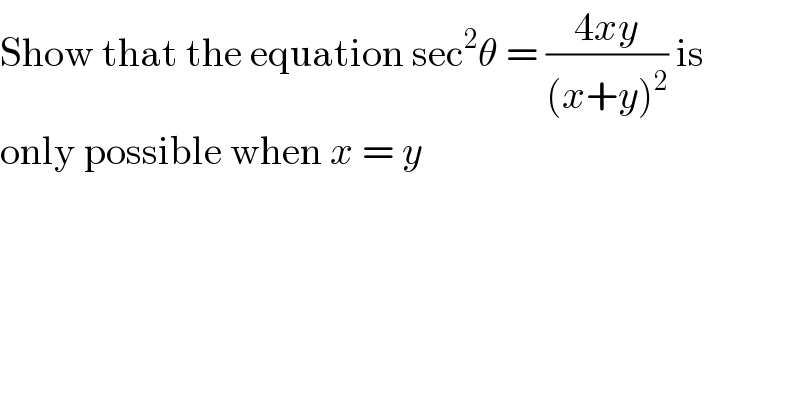
$$\mathrm{Show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{sec}^{\mathrm{2}} \theta\:=\:\frac{\mathrm{4}{xy}}{\left({x}+{y}\right)^{\mathrm{2}} }\:\mathrm{is}\: \\ $$$$\mathrm{only}\:\mathrm{possible}\:\mathrm{when}\:{x}\:=\:{y} \\ $$
Answered by math1967 last updated on 17/Jun/18
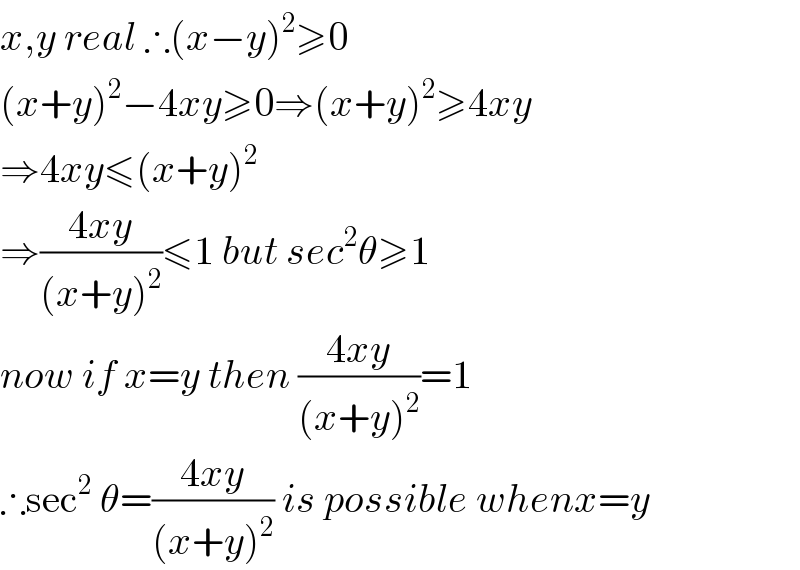
$${x},{y}\:{real}\:\therefore\left({x}−{y}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{4}{xy}\geqslant\mathrm{0}\Rightarrow\left({x}+{y}\right)^{\mathrm{2}} \geqslant\mathrm{4}{xy} \\ $$$$\Rightarrow\mathrm{4}{xy}\leqslant\left({x}+{y}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{4}{xy}}{\left({x}+{y}\right)^{\mathrm{2}} }\leqslant\mathrm{1}\:{but}\:{sec}^{\mathrm{2}} \theta\geqslant\mathrm{1} \\ $$$${now}\:{if}\:{x}={y}\:{then}\:\frac{\mathrm{4}{xy}}{\left({x}+{y}\right)^{\mathrm{2}} }=\mathrm{1} \\ $$$$\therefore\mathrm{sec}^{\mathrm{2}} \:\theta=\frac{\mathrm{4}{xy}}{\left({x}+{y}\right)^{\mathrm{2}} }\:{is}\:{possible}\:{whenx}={y} \\ $$
