Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 37344 by math khazana by abdo last updated on 12/Jun/18

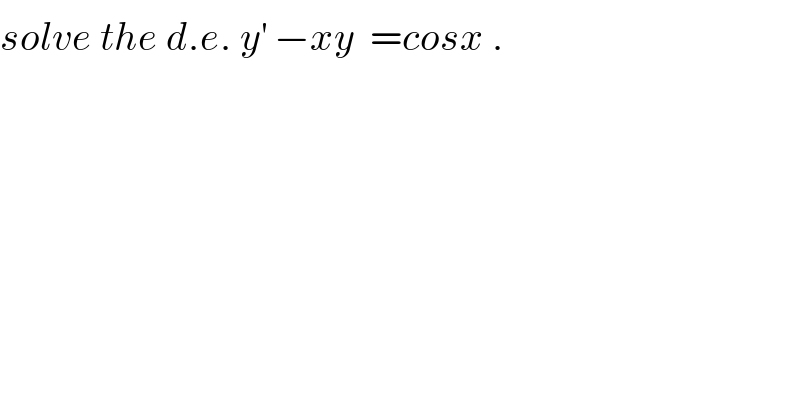
solve the d.e. y^′ −xy =cosx .

$${solve}\:{the}\:{d}.{e}.\:{y}^{'} \:−{xy}\:\:={cosx}\:. \\ $$

Commented by math khazana by abdo last updated on 12/Jun/18

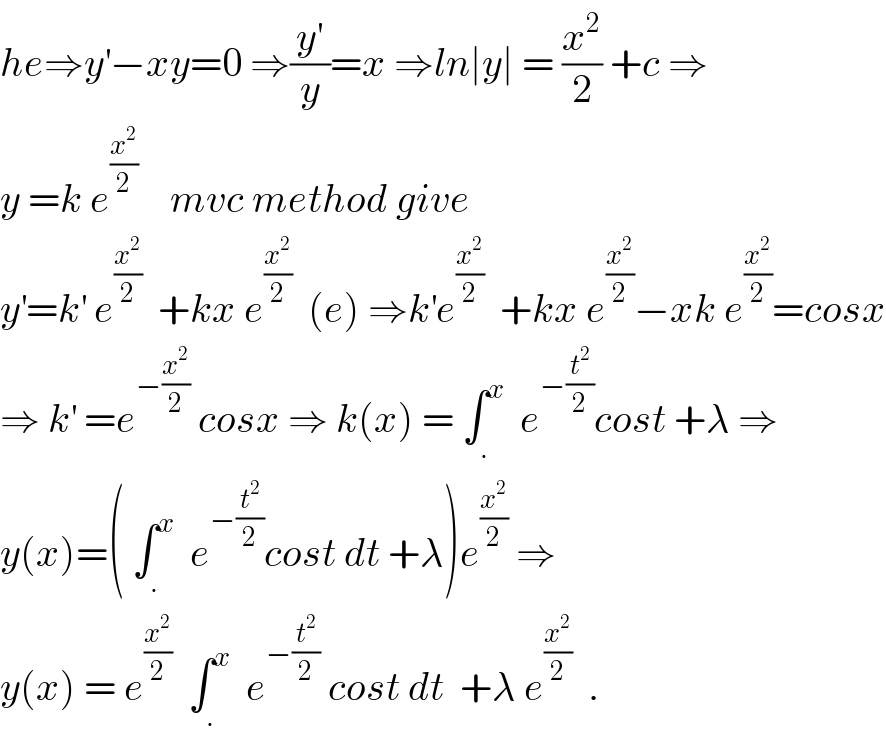
he⇒y^′ −xy=0 ⇒(y^′ /y)=x ⇒ln∣y∣ = (x^2 /2) +c ⇒ y =k e^(x^2 /2) mvc method give y^′ =k^′ e^(x^2 /2) +kx e^(x^2 /2) (e) ⇒k^′ e^(x^2 /2) +kx e^(x^2 /2) −xk e^(x^2 /2) =cosx ⇒ k^′ =e^(−(x^2 /2)) cosx ⇒ k(x) = ∫_. ^x e^(−(t^2 /2)) cost +λ ⇒ y(x)=( ∫_. ^x e^(−(t^2 /2)) cost dt +λ)e^(x^2 /2) ⇒ y(x) = e^(x^2 /2) ∫_. ^x e^(−(t^2 /2)) cost dt +λ e^(x^2 /2) .

$${he}\Rightarrow{y}^{'} −{xy}=\mathrm{0}\:\Rightarrow\frac{{y}^{'} }{{y}}={x}\:\Rightarrow{ln}\mid{y}\mid\:=\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+{c}\:\Rightarrow \\ $$$${y}\:={k}\:{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:\:\:\:{mvc}\:{method}\:{give}\: \\ $$$${y}^{'} ={k}^{'} \:{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:\:+{kx}\:{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:\:\left({e}\right)\:\Rightarrow{k}^{'} {e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:\:+{kx}\:{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} −{xk}\:{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} ={cosx} \\ $$$$\Rightarrow\:{k}^{'} \:={e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:{cosx}\:\Rightarrow\:{k}\left({x}\right)\:=\:\int_{.} ^{{x}} \:\:{e}^{−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} {cost}\:+\lambda\:\Rightarrow \\ $$$${y}\left({x}\right)=\left(\:\int_{.} ^{{x}} \:\:{e}^{−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} {cost}\:{dt}\:+\lambda\right){e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:\Rightarrow \\ $$$${y}\left({x}\right)\:=\:{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:\:\int_{.} ^{{x}} \:\:{e}^{−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} \:{cost}\:{dt}\:\:+\lambda\:{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com