
Question Number 36597 by rahul 19 last updated on 03/Jun/18
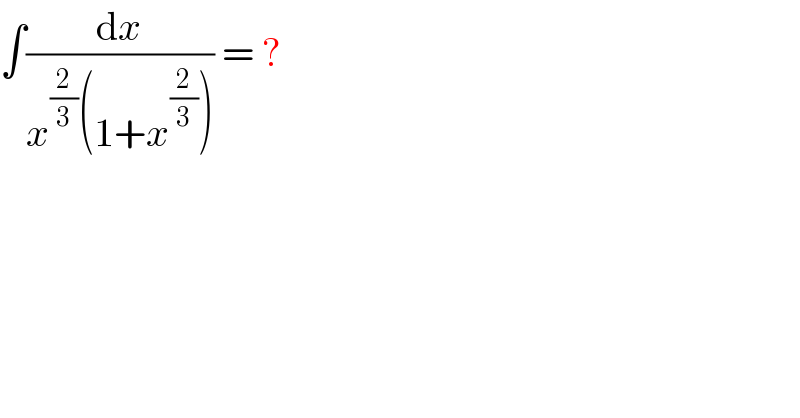
$$\int\frac{\mathrm{d}{x}}{{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \left(\mathrm{1}+{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)}\:=\:? \\ $$
Commented by rahul 19 last updated on 03/Jun/18
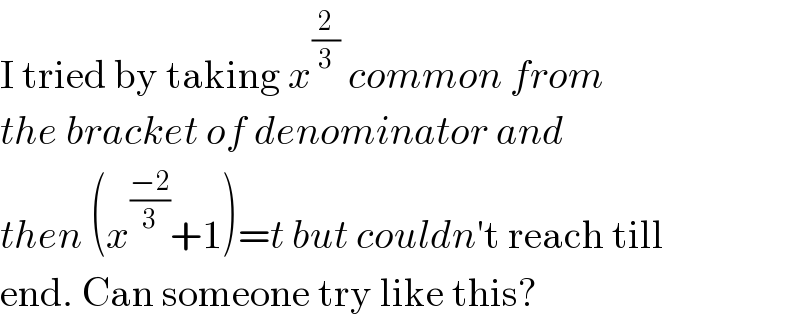
$$\mathrm{I}\:\mathrm{tried}\:\mathrm{by}\:\mathrm{taking}\:{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \:{common}\:{from} \\ $$$${the}\:{bracket}\:{of}\:{denominator}\:{and}\: \\ $$$${then}\:\left({x}^{\frac{−\mathrm{2}}{\mathrm{3}}} +\mathrm{1}\right)={t}\:{but}\:{couldn}'\mathrm{t}\:\mathrm{reach}\:\mathrm{till} \\ $$$$\mathrm{end}.\:\mathrm{Can}\:\mathrm{someone}\:\mathrm{try}\:\mathrm{like}\:\mathrm{this}? \\ $$
Commented by abdo mathsup 649 cc last updated on 03/Jun/18
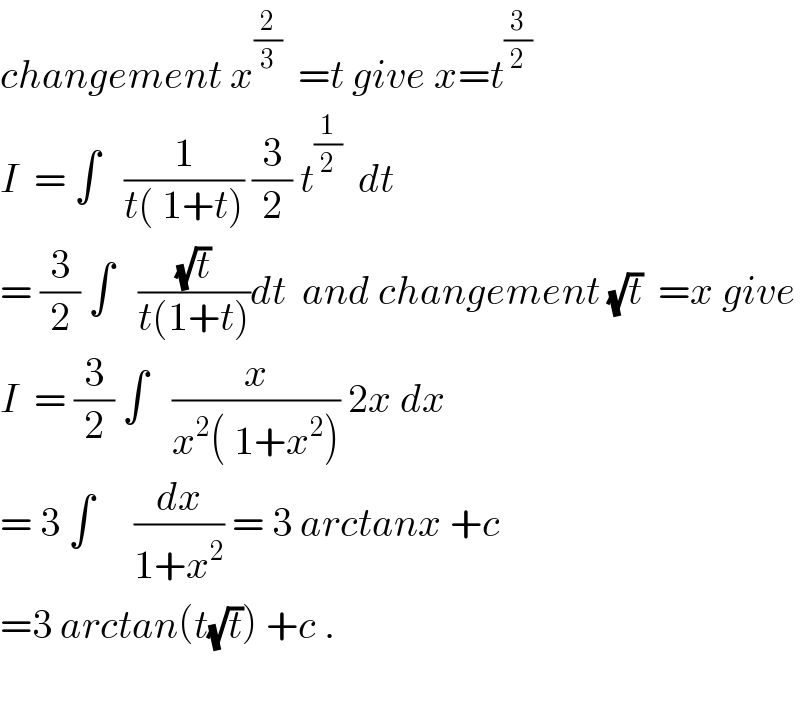
$${changement}\:{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \:\:={t}\:{give}\:{x}={t}^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$${I}\:\:=\:\int\:\:\:\frac{\mathrm{1}}{{t}\left(\:\mathrm{1}+{t}\right)}\:\frac{\mathrm{3}}{\mathrm{2}}\:{t}^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:{dt} \\ $$$$=\:\frac{\mathrm{3}}{\mathrm{2}}\:\int\:\:\:\frac{\sqrt{{t}}}{{t}\left(\mathrm{1}+{t}\right)}{dt}\:\:{and}\:{changement}\:\sqrt{{t}}\:\:={x}\:{give} \\ $$$${I}\:\:=\:\frac{\mathrm{3}}{\mathrm{2}}\:\int\:\:\:\frac{{x}}{{x}^{\mathrm{2}} \left(\:\mathrm{1}+{x}^{\mathrm{2}} \right)}\:\mathrm{2}{x}\:{dx} \\ $$$$=\:\mathrm{3}\:\int\:\:\:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:=\:\mathrm{3}\:{arctanx}\:+{c} \\ $$$$=\mathrm{3}\:{arctan}\left({t}\sqrt{{t}}\right)\:+{c}\:. \\ $$$$ \\ $$
Answered by Joel579 last updated on 03/Jun/18
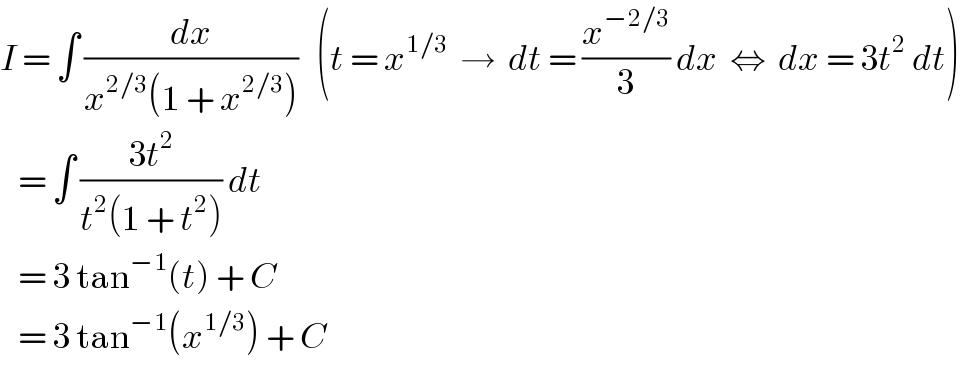
$${I}\:=\:\int\:\frac{{dx}}{{x}^{\mathrm{2}/\mathrm{3}} \left(\mathrm{1}\:+\:{x}^{\mathrm{2}/\mathrm{3}} \right)}\:\:\:\left({t}\:=\:{x}^{\mathrm{1}/\mathrm{3}} \:\:\rightarrow\:\:{dt}\:=\:\frac{{x}^{−\mathrm{2}/\mathrm{3}} }{\mathrm{3}}\:{dx}\:\:\Leftrightarrow\:\:{dx}\:=\:\mathrm{3}{t}^{\mathrm{2}} \:{dt}\right) \\ $$$$\:\:\:=\:\int\:\frac{\mathrm{3}{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} \left(\mathrm{1}\:+\:{t}^{\mathrm{2}} \right)}\:{dt} \\ $$$$\:\:\:=\:\mathrm{3}\:\mathrm{tan}^{−\mathrm{1}} \left({t}\right)\:+\:{C} \\ $$$$\:\:\:=\:\mathrm{3}\:\mathrm{tan}^{−\mathrm{1}} \left({x}^{\mathrm{1}/\mathrm{3}} \right)\:+\:{C} \\ $$
Answered by sma3l2996 last updated on 03/Jun/18
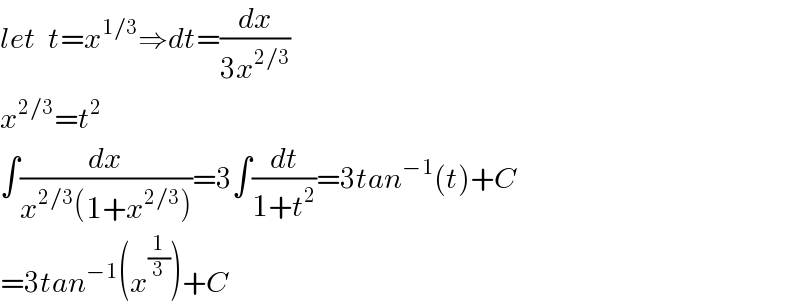
$${let}\:\:{t}={x}^{\mathrm{1}/\mathrm{3}} \Rightarrow{dt}=\frac{{dx}}{\mathrm{3}{x}^{\mathrm{2}/\mathrm{3}} } \\ $$$${x}^{\mathrm{2}/\mathrm{3}} ={t}^{\mathrm{2}} \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{2}/\mathrm{3}} \left(\mathrm{1}+{x}^{\mathrm{2}/\mathrm{3}} \right)}=\mathrm{3}\int\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }=\mathrm{3}{tan}^{−\mathrm{1}} \left({t}\right)+{C} \\ $$$$=\mathrm{3}{tan}^{−\mathrm{1}} \left({x}^{\frac{\mathrm{1}}{\mathrm{3}}} \right)+{C} \\ $$
