
Question Number 35338 by jasno91 last updated on 18/May/18
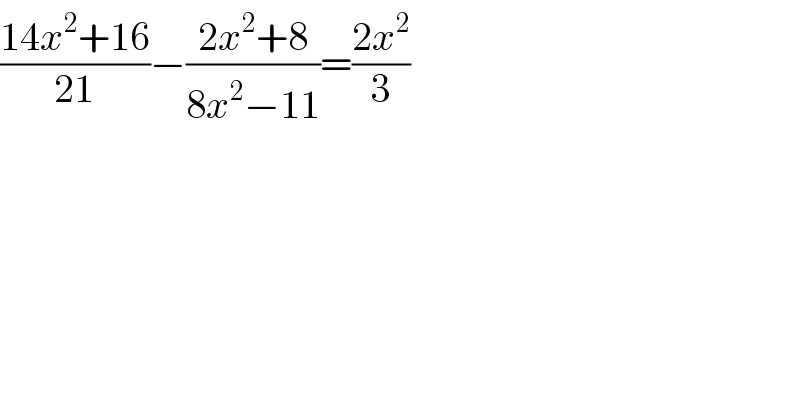
$$\frac{\mathrm{14}{x}^{\mathrm{2}} +\mathrm{16}}{\mathrm{21}}−\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{8}}{\mathrm{8}{x}^{\mathrm{2}} −\mathrm{11}}=\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{3}} \\ $$
Commented by Rasheed.Sindhi last updated on 18/May/18
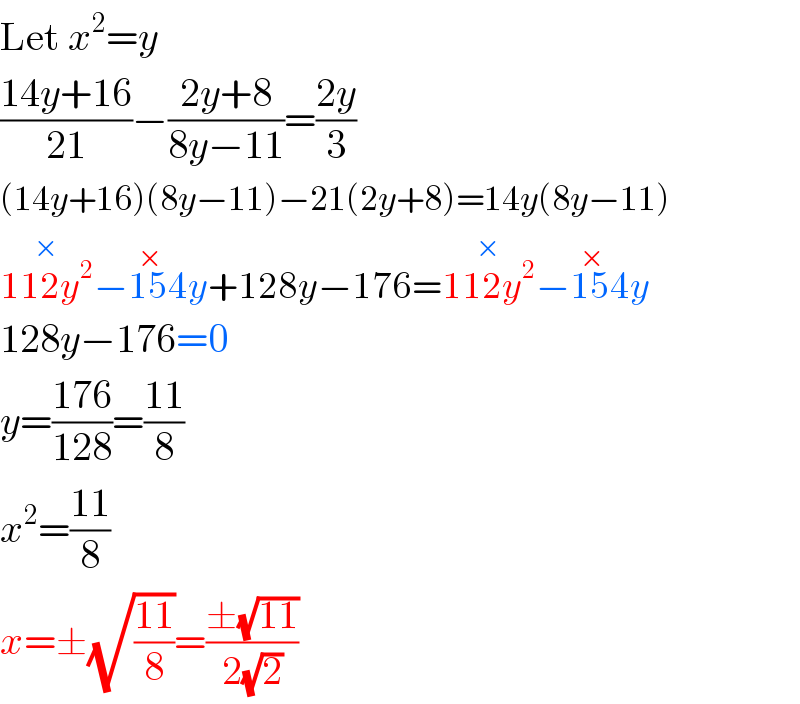
$$\mathrm{Let}\:{x}^{\mathrm{2}} ={y} \\ $$$$\frac{\mathrm{14}{y}+\mathrm{16}}{\mathrm{21}}−\frac{\mathrm{2}{y}+\mathrm{8}}{\mathrm{8}{y}−\mathrm{11}}=\frac{\mathrm{2}{y}}{\mathrm{3}} \\ $$$$\left(\mathrm{14}{y}+\mathrm{16}\right)\left(\mathrm{8}{y}−\mathrm{11}\right)−\mathrm{21}\left(\mathrm{2}{y}+\mathrm{8}\right)=\mathrm{14}{y}\left(\mathrm{8}{y}−\mathrm{11}\right) \\ $$$$\overset{×} {\mathrm{112}{y}^{\mathrm{2}} }\overset{×} {−\mathrm{154}{y}}+\mathrm{128}{y}−\mathrm{176}=\overset{×} {\mathrm{112}{y}^{\mathrm{2}} }\overset{×} {−\mathrm{154}{y}} \\ $$$$\mathrm{128}{y}−\mathrm{176}=\mathrm{0} \\ $$$${y}=\frac{\mathrm{176}}{\mathrm{128}}=\frac{\mathrm{11}}{\mathrm{8}} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{11}}{\mathrm{8}} \\ $$$${x}=\pm\sqrt{\frac{\mathrm{11}}{\mathrm{8}}}=\frac{\pm\sqrt{\mathrm{11}}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$
