
Previous in Electric Current and Circuits Next in Electric Current and Circuits
Question Number 34587 by ajfour last updated on 08/May/18
Commented by ajfour last updated on 09/May/18
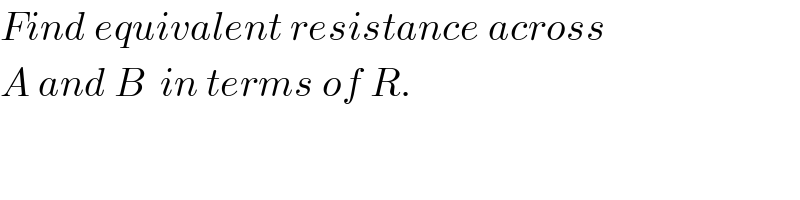
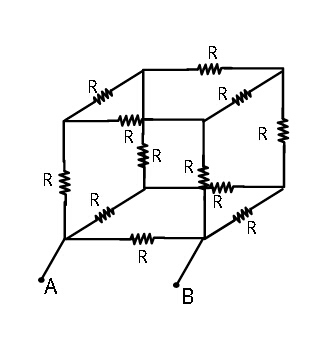
$${Find}\:{equivalent}\:{resistance}\:{across} \\ $$$${A}\:{and}\:{B}\:\:{in}\:{terms}\:{of}\:{R}. \\ $$
Answered by ajfour last updated on 09/May/18
Commented by ajfour last updated on 09/May/18

$${R}_{{eq}} =\:\frac{\mathrm{7}{R}}{\mathrm{12}}\:\:. \\ $$
Commented by MJS last updated on 09/May/18

$$\mathrm{is}\:\mathrm{the}\:\mathrm{left}\:\mathrm{scetch}\:\mathrm{complete}?\:\mathrm{the}\:\mathrm{cube}\:\mathrm{has} \\ $$$$\mathrm{got}\:\mathrm{8}\:\mathrm{points},\:\mathrm{here}\:\mathrm{I}\:\mathrm{only}\:\mathrm{see}\:\mathrm{6}... \\ $$$$\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{good}\:\mathrm{in}\:\mathrm{these}\:\mathrm{things},\:\mathrm{so}\:\mathrm{please} \\ $$$$\mathrm{correct}\:\mathrm{my}\:\mathrm{answer} \\ $$
Commented by ajfour last updated on 09/May/18
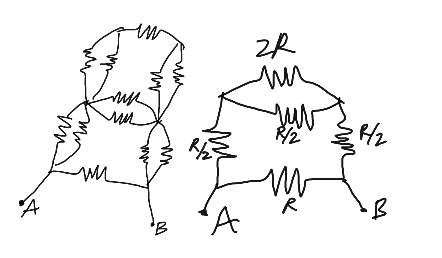
Commented by ajfour last updated on 09/May/18

$${C}\:{and}\:{D}\:{are}\:{equipotential}\:{points} \\ $$$${and}\:{can}\:{be}\:{brought}\:{together}. \\ $$$${E},\:{F}\:\:{are}\:{also}\:{equipotential}\:{points}; \\ $$$${and}\:{so}\:{are}\:{brought}\:{together}\:{in}\:{the} \\ $$$${left}\:{sketch}. \\ $$
Commented by MJS last updated on 09/May/18

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by rahul 19 last updated on 09/May/18
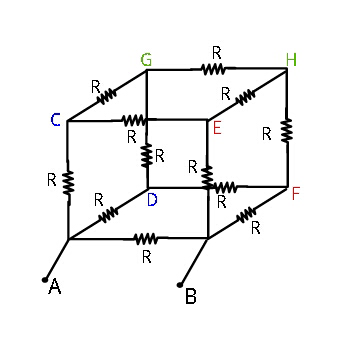
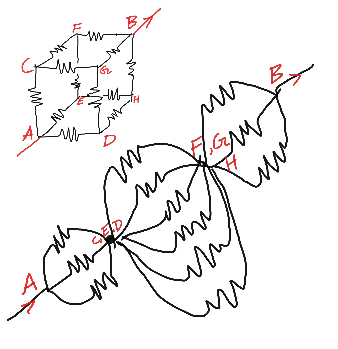
Find equivalent resistance across the following in the above figure : 1) F and C 2) F and G in terms of R. ����
Commented by rahul 19 last updated on 11/May/18

$${Anyone}\:? \\ $$
Commented by ajfour last updated on 11/May/18
$${see}\:{below}\:{for}\:\left(\mathrm{1}\right)\:\:\: \\ $$$${points}\:{renamed}\:{see}\:{figure}. \\ $$
Answered by ajfour last updated on 11/May/18
Commented by ajfour last updated on 12/May/18
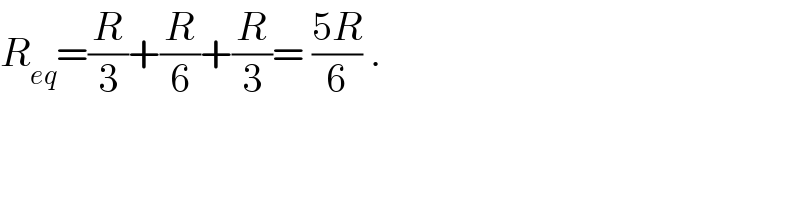
$${R}_{{eq}} =\frac{{R}}{\mathrm{3}}+\frac{{R}}{\mathrm{6}}+\frac{{R}}{\mathrm{3}}=\:\frac{\mathrm{5}{R}}{\mathrm{6}}\:. \\ $$
Commented by rahul 19 last updated on 12/May/18

$${Thank}\:{you}\:{sir}. \\ $$
