
Question Number 34159 by candre last updated on 01/May/18
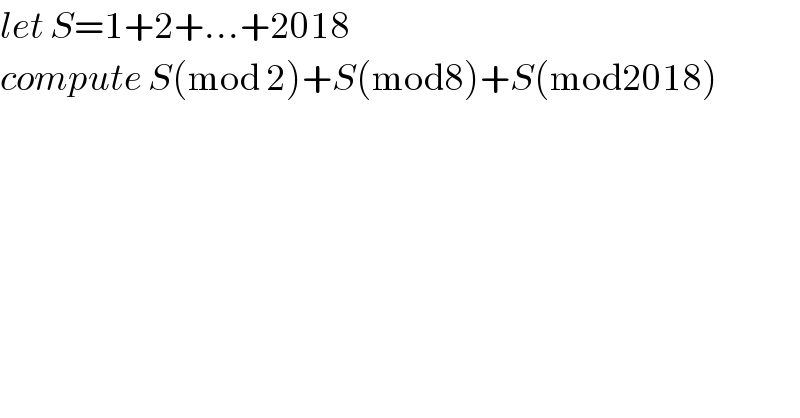
$${let}\:{S}=\mathrm{1}+\mathrm{2}+...+\mathrm{2018} \\ $$$${compute}\:{S}\left(\mathrm{mod}\:\mathrm{2}\right)+{S}\left(\mathrm{mod8}\right)+{S}\left(\mathrm{mod2018}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 05/May/18

$$\mathrm{S}=\left(\mathrm{1}+\mathrm{3}+\mathrm{5}+...+\mathrm{2017}\right)+\left(\mathrm{2}+\mathrm{4}+...+\mathrm{2018}\right) \\ $$$$\mathrm{Sum}\:\mathrm{of}\:\mathrm{even}\:\mathrm{numbers}\:\mathrm{is}\:\mathrm{even}\:\mathrm{number} \\ $$$$\:\:\:\:\:\therefore\:\mathrm{2}+\mathrm{4}+...+\mathrm{2018}\:\mathrm{even}\:\mathrm{number} \\ $$$$\mathrm{Sum}\:\mathrm{of}\:\mathrm{odd}\:\mathrm{numbers},\mathrm{when}\:\mathrm{number}\:\mathrm{of} \\ $$$$\mathrm{numbers}\:\mathrm{is}\:\mathrm{odd},\:\mathrm{is}\:\mathrm{odd}. \\ $$$$\:\:\:\:\therefore\:\mathrm{1}+\mathrm{3}+\mathrm{5}+...+\mathrm{2017}\:\mathrm{is}\:\mathrm{odd}\:\mathrm{number} \\ $$$$\:\:\therefore\mathrm{S}=\mathrm{odd}+\mathrm{even}=\mathrm{odd}\:\mathrm{number} \\ $$$$\therefore\:\mathrm{S}\left(\mathrm{mod2}\right)=\mathrm{1} \\ $$$$−−−−− \\ $$$$\mathrm{S}\left(\mathrm{mod8}\right)? \\ $$$$−−−−−− \\ $$$$\mathrm{S}=\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\mathrm{2017}\right)+\mathrm{2018} \\ $$$$\:\:\:=\left(\mathrm{1}+\mathrm{2017}\right)+\left(\mathrm{2}+\mathrm{2016}\right)+...+\mathrm{1009}+\mathrm{2018} \\ $$$$\:\:\:=\mathrm{2018}+\mathrm{2018}+...+\mathrm{1009}+\mathrm{2018} \\ $$$$\:\:\:=\left(\mathrm{multiple}\:\mathrm{of}\:\mathrm{2018}\right)+\mathrm{1009} \\ $$$$\therefore\:\mathrm{S}\left(\mathrm{mod}\:\mathrm{2018}\right)=\mathrm{1009} \\ $$$$\mathrm{Continue} \\ $$
Answered by Rasheed.Sindhi last updated on 05/May/18
![S=1+2+...+2018; an AP:a=1,d=1,n=2018 S=(n/2)[2a+(n−1)d] S=((2018)/2)[2(1)+(2018−1)(1)] =1009[2018+1] =2018×1009+1009 ∴S(mod2018)=1009.........A −−−−−−−−−−− S=1009×2019 =(1008+1)(2018+1) =1008×2018+1008+2018+1 =1008×2019+2018+1 =2(504×2019+1009)+1 ∴S(mod 2)=1................B −−−−−− S=1009×2019 =(1009)(2000+16+3) =2000×1009+16×1009+3×1009 =2000×1009+16×1009+3000+27 =2000×1009+16×1009+3000+24+3 2000,16,3000 & 24 are divisible by 8 [Complete thousands are always divisible by8] ∴ S(mod 8)=3...............C From A,B &C S(mod 2)+S(mod 8)+S(mod 2018) =1+3+1009=1013](Q34353.png)
$$\mathrm{S}=\mathrm{1}+\mathrm{2}+...+\mathrm{2018};\:\mathrm{an}\:\mathrm{AP}:{a}=\mathrm{1},\mathrm{d}=\mathrm{1},\mathrm{n}=\mathrm{2018} \\ $$$$\mathrm{S}=\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{a}+\left({n}−\mathrm{1}\right){d}\right] \\ $$$$\mathrm{S}=\frac{\mathrm{2018}}{\mathrm{2}}\left[\mathrm{2}\left(\mathrm{1}\right)+\left(\mathrm{2018}−\mathrm{1}\right)\left(\mathrm{1}\right)\right] \\ $$$$\:\:\:\:=\mathrm{1009}\left[\mathrm{2018}+\mathrm{1}\right] \\ $$$$\:\:\:\:=\mathrm{2018}×\mathrm{1009}+\mathrm{1009} \\ $$$$\therefore\mathrm{S}\left(\mathrm{mod2018}\right)=\mathrm{1009}.........\mathrm{A} \\ $$$$−−−−−−−−−−− \\ $$$$\mathrm{S}=\mathrm{1009}×\mathrm{2019} \\ $$$$\:\:\:=\left(\mathrm{1008}+\mathrm{1}\right)\left(\mathrm{2018}+\mathrm{1}\right) \\ $$$$\:\:\:=\mathrm{1008}×\mathrm{2018}+\mathrm{1008}+\mathrm{2018}+\mathrm{1} \\ $$$$\:\:\:=\mathrm{1008}×\mathrm{2019}+\mathrm{2018}+\mathrm{1} \\ $$$$\:\:\:=\mathrm{2}\left(\mathrm{504}×\mathrm{2019}+\mathrm{1009}\right)+\mathrm{1} \\ $$$$\therefore\mathrm{S}\left(\mathrm{mod}\:\mathrm{2}\right)=\mathrm{1}................\mathrm{B} \\ $$$$−−−−−− \\ $$$$\mathrm{S}=\mathrm{1009}×\mathrm{2019} \\ $$$$\:\:\:=\left(\mathrm{1009}\right)\left(\mathrm{2000}+\mathrm{16}+\mathrm{3}\right) \\ $$$$\:\:\:=\mathrm{2000}×\mathrm{1009}+\mathrm{16}×\mathrm{1009}+\mathrm{3}×\mathrm{1009} \\ $$$$\:\:\:=\mathrm{2000}×\mathrm{1009}+\mathrm{16}×\mathrm{1009}+\mathrm{3000}+\mathrm{27} \\ $$$$\:\:\:=\mathrm{2000}×\mathrm{1009}+\mathrm{16}×\mathrm{1009}+\mathrm{3000}+\mathrm{24}+\mathrm{3} \\ $$$$\mathrm{2000},\mathrm{16},\mathrm{3000}\:\&\:\mathrm{24}\:\mathrm{are}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{8} \\ $$$$\:\left[\mathrm{Complete}\:\mathrm{thousands}\:\mathrm{are}\:\mathrm{always}\:\mathrm{divisible}\right. \\ $$$$\left.\mathrm{by8}\right] \\ $$$$\therefore\:\mathrm{S}\left(\mathrm{mod}\:\mathrm{8}\right)=\mathrm{3}...............\mathrm{C} \\ $$$$\mathrm{From}\:\mathrm{A},\mathrm{B}\:\&\mathrm{C}\: \\ $$$$\mathrm{S}\left(\mathrm{mod}\:\mathrm{2}\right)+\mathrm{S}\left(\mathrm{mod}\:\mathrm{8}\right)+\mathrm{S}\left(\mathrm{mod}\:\mathrm{2018}\right) \\ $$$$\:\:\:\:\:\:=\mathrm{1}+\mathrm{3}+\mathrm{1009}=\mathrm{1013} \\ $$
Commented by Rasheed.Sindhi last updated on 09/May/18

$$\mathrm{Mr}.\:\mathrm{candre}\:\mathrm{please}\:\mathrm{confirm}\:\mathrm{the}\:\mathrm{answer}. \\ $$
