
Question Number 34031 by naka3546 last updated on 29/Apr/18
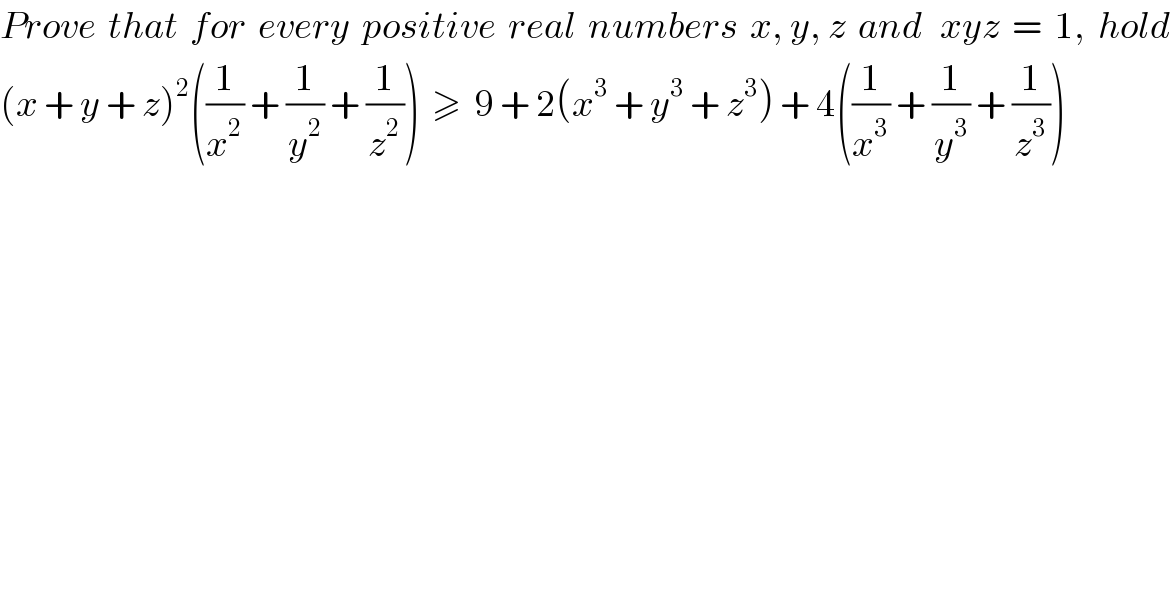
$${Prove}\:\:{that}\:\:{for}\:\:{every}\:\:{positive}\:\:{real}\:\:{numbers}\:\:{x},\:{y},\:{z}\:\:{and}\:\:\:{xyz}\:\:=\:\:\mathrm{1},\:\:{hold} \\ $$$$\left({x}\:+\:{y}\:+\:{z}\right)^{\mathrm{2}} \left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{{z}^{\mathrm{2}} }\right)\:\:\geqslant\:\:\mathrm{9}\:+\:\mathrm{2}\left({x}^{\mathrm{3}} \:+\:{y}^{\mathrm{3}} \:+\:{z}^{\mathrm{3}} \right)\:+\:\mathrm{4}\left(\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:+\:\frac{\mathrm{1}}{{y}^{\mathrm{3}} }\:+\:\frac{\mathrm{1}}{{z}^{\mathrm{3}} }\right)\: \\ $$
