Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 33940 by rahul 19 last updated on 28/Apr/18

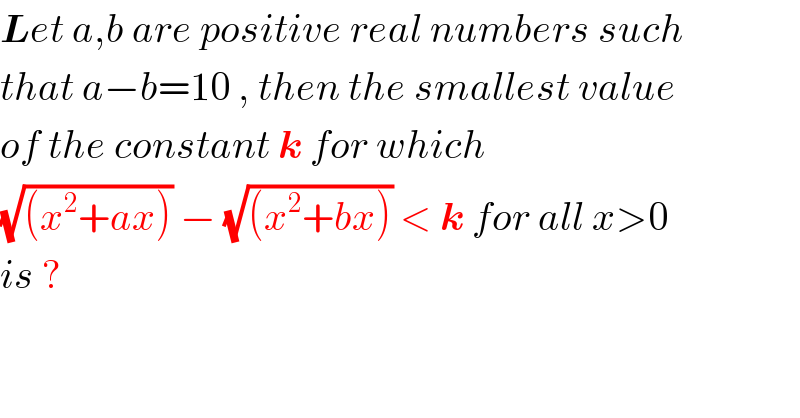
Let a,b are positive real numbers such that a−b=10 , then the smallest value of the constant k for which (√((x^2 +ax))) − (√((x^2 +bx))) < k for all x>0 is ?

$$\boldsymbol{{L}}{et}\:{a},{b}\:{are}\:{positive}\:{real}\:{numbers}\:{such} \\ $$ $${that}\:{a}−{b}=\mathrm{10}\:,\:{then}\:{the}\:{smallest}\:{value} \\ $$ $${of}\:{the}\:{constant}\:\boldsymbol{{k}}\:{for}\:{which}\: \\ $$ $$\sqrt{\left({x}^{\mathrm{2}} +{ax}\right)}\:−\:\sqrt{\left({x}^{\mathrm{2}} +{bx}\right)}\:<\:\boldsymbol{{k}}\:{for}\:{all}\:{x}>\mathrm{0}\: \\ $$ $${is}\:? \\ $$

Answered by MJS last updated on 28/Apr/18

a=r+5 b=r−5 (√(x^2 +rx+5x))−(√(x^2 +rx−5x))<k we have to show that lim_(x→∞) (√(x^2 +rx+5x))−(√(x^2 +rx−5x))=5 sorry I have no time right now... (√(x^2 +rx+5x))−(√(x^2 +rx−5x))=k (I.) [x=y ⇒ (1/x)=(1/y)] (1/((√(x^2 +rx+5x))−(√(x^2 +rx−5x))))=(1/k) [(1/(u−v))=((u+v)/((u−v)(u+v)))=((u+v)/(u^2 −v^2 ))] (((√(x^2 +rx+5x))+(√(x^2 +rx−5x)))/(x^2 +rx+5x−(x^2 +rx−5x)))=(1/k) (((√(x^2 +rx+5x))+(√(x^2 +rx−5x)))/(10x))=(1/k) (√(x^2 +rx+5x))+(√(x^2 +rx−5x))=((10x)/k) (II.) 2(√(x^2 +rx+5x))=k+((10x)/k) (I.+II.) 4(x^2 +rx+5x)=k^2 +20x+((100x^2 )/k^2 ) (4−((100)/k^2 ))x^2 +4rx−k^2 =0 x^2 +((k^2 r)/(k^2 −25))x−(k^4 /(4(k^2 −25)))=0 x=−((k^2 r)/(2(k^2 −25)))±(k^2 /(2(k^2 −25)))(√(k^2 +r^2 −25))= =((r±(√(k^2 +r^2 −25)))/(2(k^2 −25)))k^2 (1/x)=((2(k^2 −25))/(r±(√(k^2 +r^2 −25))))×(1/k^2 ) x→∞ ⇒ k^2 −25=0 ⇒ k=±5 (√(x^2 +rx+5x))−(√(x^2 +rx−5x))>0 ⇒ k=5

$${a}={r}+\mathrm{5} \\ $$ $${b}={r}−\mathrm{5} \\ $$ $$\sqrt{{x}^{\mathrm{2}} +{rx}+\mathrm{5}{x}}−\sqrt{{x}^{\mathrm{2}} +{rx}−\mathrm{5}{x}}<{k} \\ $$ $$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{show}\:\mathrm{that} \\ $$ $$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt{{x}^{\mathrm{2}} +{rx}+\mathrm{5}{x}}−\sqrt{{x}^{\mathrm{2}} +{rx}−\mathrm{5}{x}}=\mathrm{5} \\ $$ $$\mathrm{sorry}\:\mathrm{I}\:\mathrm{have}\:\mathrm{no}\:\mathrm{time}\:\mathrm{right}\:\mathrm{now}... \\ $$ $$ \\ $$ $$ \\ $$ $$\sqrt{{x}^{\mathrm{2}} +{rx}+\mathrm{5}{x}}−\sqrt{{x}^{\mathrm{2}} +{rx}−\mathrm{5}{x}}={k}\:\:\:\:\:\left({I}.\right) \\ $$ $$\:\:\:\:\:\:\:\:\:\:\left[{x}={y}\:\Rightarrow\:\frac{\mathrm{1}}{{x}}=\frac{\mathrm{1}}{{y}}\right] \\ $$ $$\frac{\mathrm{1}}{\sqrt{{x}^{\mathrm{2}} +{rx}+\mathrm{5}{x}}−\sqrt{{x}^{\mathrm{2}} +{rx}−\mathrm{5}{x}}}=\frac{\mathrm{1}}{{k}} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\left[\frac{\mathrm{1}}{{u}−{v}}=\frac{{u}+{v}}{\left({u}−{v}\right)\left({u}+{v}\right)}=\frac{{u}+{v}}{{u}^{\mathrm{2}} −{v}^{\mathrm{2}} }\right] \\ $$ $$\frac{\sqrt{{x}^{\mathrm{2}} +{rx}+\mathrm{5}{x}}+\sqrt{{x}^{\mathrm{2}} +{rx}−\mathrm{5}{x}}}{{x}^{\mathrm{2}} +{rx}+\mathrm{5}{x}−\left({x}^{\mathrm{2}} +{rx}−\mathrm{5}{x}\right)}=\frac{\mathrm{1}}{{k}} \\ $$ $$\frac{\sqrt{{x}^{\mathrm{2}} +{rx}+\mathrm{5}{x}}+\sqrt{{x}^{\mathrm{2}} +{rx}−\mathrm{5}{x}}}{\mathrm{10}{x}}=\frac{\mathrm{1}}{{k}} \\ $$ $$\sqrt{{x}^{\mathrm{2}} +{rx}+\mathrm{5}{x}}+\sqrt{{x}^{\mathrm{2}} +{rx}−\mathrm{5}{x}}=\frac{\mathrm{10}{x}}{{k}}\:\:\:\:\:\left({II}.\right) \\ $$ $$\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{rx}+\mathrm{5}{x}}={k}+\frac{\mathrm{10}{x}}{{k}}\:\:\:\:\:\left({I}.+{II}.\right) \\ $$ $$\mathrm{4}\left({x}^{\mathrm{2}} +{rx}+\mathrm{5}{x}\right)={k}^{\mathrm{2}} +\mathrm{20}{x}+\frac{\mathrm{100}{x}^{\mathrm{2}} }{{k}^{\mathrm{2}} } \\ $$ $$\left(\mathrm{4}−\frac{\mathrm{100}}{{k}^{\mathrm{2}} }\right){x}^{\mathrm{2}} +\mathrm{4}{rx}−{k}^{\mathrm{2}} =\mathrm{0} \\ $$ $${x}^{\mathrm{2}} +\frac{{k}^{\mathrm{2}} {r}}{{k}^{\mathrm{2}} −\mathrm{25}}{x}−\frac{{k}^{\mathrm{4}} }{\mathrm{4}\left({k}^{\mathrm{2}} −\mathrm{25}\right)}=\mathrm{0} \\ $$ $${x}=−\frac{{k}^{\mathrm{2}} {r}}{\mathrm{2}\left({k}^{\mathrm{2}} −\mathrm{25}\right)}\pm\frac{{k}^{\mathrm{2}} }{\mathrm{2}\left({k}^{\mathrm{2}} −\mathrm{25}\right)}\sqrt{{k}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{25}}= \\ $$ $$=\frac{{r}\pm\sqrt{{k}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{25}}}{\mathrm{2}\left({k}^{\mathrm{2}} −\mathrm{25}\right)}{k}^{\mathrm{2}} \\ $$ $$\frac{\mathrm{1}}{{x}}=\frac{\mathrm{2}\left({k}^{\mathrm{2}} −\mathrm{25}\right)}{{r}\pm\sqrt{{k}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{25}}}×\frac{\mathrm{1}}{{k}^{\mathrm{2}} } \\ $$ $${x}\rightarrow\infty\:\Rightarrow\:{k}^{\mathrm{2}} −\mathrm{25}=\mathrm{0}\:\Rightarrow\:{k}=\pm\mathrm{5} \\ $$ $$\sqrt{{x}^{\mathrm{2}} +{rx}+\mathrm{5}{x}}−\sqrt{{x}^{\mathrm{2}} +{rx}−\mathrm{5}{x}}>\mathrm{0}\:\Rightarrow\:{k}=\mathrm{5} \\ $$

Commented byrahul 19 last updated on 28/Apr/18

No problem sir. btw, how you came to know it should be equal to 5?

$${No}\:\mathrm{problem}\:\mathrm{sir}.\: \\ $$ $$\mathrm{btw},\:{how}\:{you}\:{came}\:{to}\:{know}\:{it}\:{should} \\ $$ $${be}\:{equal}\:{to}\:\mathrm{5}? \\ $$

Commented byMJS last updated on 28/Apr/18

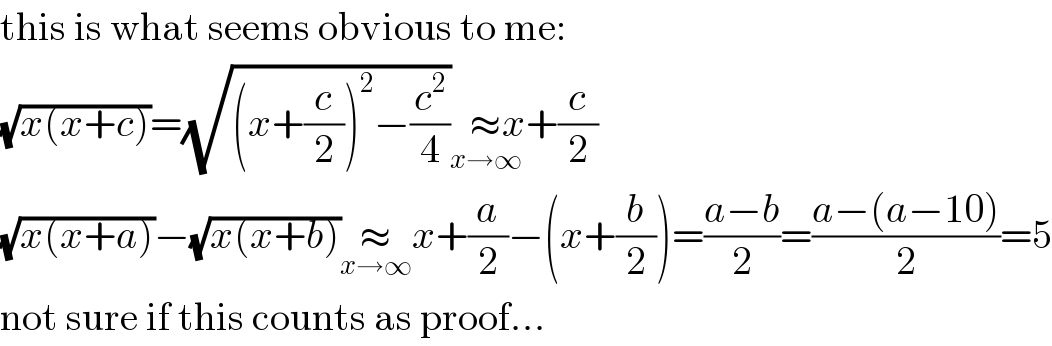
this is what seems obvious to me: (√(x(x+c)))=(√((x+(c/2))^2 −(c^2 /4)))≈_(x→∞) x+(c/2) (√(x(x+a)))−(√(x(x+b)))≈_(x→∞) x+(a/2)−(x+(b/2))=((a−b)/2)=((a−(a−10))/2)=5 not sure if this counts as proof...

$$\mathrm{this}\:\mathrm{is}\:\mathrm{what}\:\mathrm{seems}\:\mathrm{obvious}\:\mathrm{to}\:\mathrm{me}: \\ $$ $$\sqrt{{x}\left({x}+{c}\right)}=\sqrt{\left({x}+\frac{{c}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{{c}^{\mathrm{2}} }{\mathrm{4}}}\underset{{x}\rightarrow\infty} {\approx}{x}+\frac{{c}}{\mathrm{2}} \\ $$ $$\sqrt{{x}\left({x}+{a}\right)}−\sqrt{{x}\left({x}+{b}\right)}\underset{{x}\rightarrow\infty} {\approx}{x}+\frac{{a}}{\mathrm{2}}−\left({x}+\frac{{b}}{\mathrm{2}}\right)=\frac{{a}−{b}}{\mathrm{2}}=\frac{{a}−\left({a}−\mathrm{10}\right)}{\mathrm{2}}=\mathrm{5} \\ $$ $$\mathrm{not}\:\mathrm{sure}\:\mathrm{if}\:\mathrm{this}\:\mathrm{counts}\:\mathrm{as}\:\mathrm{proof}... \\ $$

Commented byrahul 19 last updated on 28/Apr/18

Thank you sir .

$$\mathscr{T}{hank}\:\mathrm{you}\:\mathrm{sir}\:. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 28/Apr/18

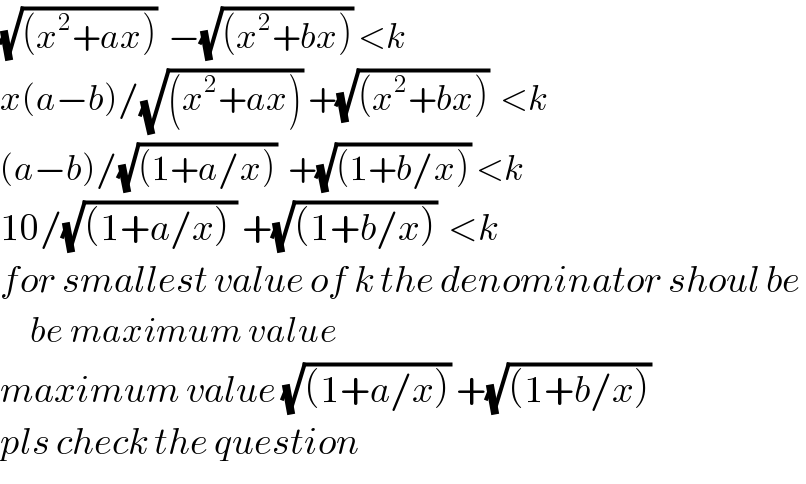
(√((x^2 +ax))) −(√((x^2 +bx))) <k x(a−b)/(√((x_ ^2 +ax))) +(√((x^2 +bx))) <k (a−b)/(√((1+a/x))) +(√((1+b/x))) <k 10/(√((1+a/x) )) +(√((1+b/x))) <k for smallest value of k the denominator shoul be be maximum value maximum value (√((1+a/x))) +(√((1+b/x))) pls check the question

$$\sqrt{\left({x}^{\mathrm{2}} +{ax}\right)}\:\:−\sqrt{\left({x}^{\mathrm{2}} +{bx}\right)}\:<{k} \\ $$ $${x}\left({a}−{b}\right)/\sqrt{\left({x}_{} ^{\mathrm{2}} +{ax}\right)}\:+\sqrt{\left({x}^{\mathrm{2}} +{bx}\right)}\:\:<{k} \\ $$ $$\left({a}−{b}\right)/\sqrt{\left(\mathrm{1}+{a}/{x}\right)}\:\:+\sqrt{\left(\mathrm{1}+{b}/{x}\right)}\:<{k} \\ $$ $$\mathrm{10}/\sqrt{\left(\mathrm{1}+{a}/{x}\right)\:}\:+\sqrt{\left(\mathrm{1}+{b}/{x}\right)}\:\:<{k} \\ $$ $${for}\:{smallest}\:{value}\:{of}\:{k}\:{the}\:{denominator}\:{shoul}\:{be}\: \\ $$ $$\:\:\:\:\:{be}\:{maximum}\:{value} \\ $$ $${maximum}\:{value}\:\sqrt{\left(\mathrm{1}+{a}/{x}\right)}\:+\sqrt{\left(\mathrm{1}+{b}/{x}\right)} \\ $$ $${pls}\:{check}\:{the}\:{question} \\ $$

Commented byrahul 19 last updated on 28/Apr/18

Wow! nice solution sir!

$${Wow}!\:{nice}\:{solution}\:{sir}! \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 28/Apr/18

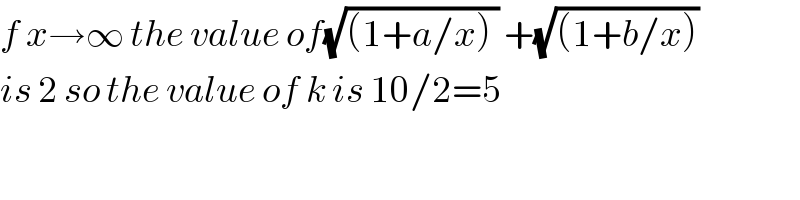
f x→∞ the value of(√((1+a/x) )) +(√((1+b/x))) is 2 so the value of k is 10/2=5

$${f}\:{x}\rightarrow\infty\:{the}\:{value}\:{of}\sqrt{\left(\mathrm{1}+{a}/{x}\right)\:}\:+\sqrt{\left(\mathrm{1}+{b}/{x}\right)} \\ $$ $${is}\:\mathrm{2}\:{so}\:{the}\:{value}\:{of}\:{k}\:{is}\:\mathrm{10}/\mathrm{2}=\mathrm{5} \\ $$

Commented byrahul 19 last updated on 29/Apr/18

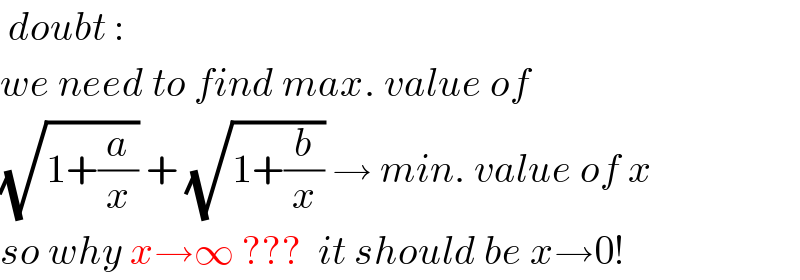
doubt : we need to find max. value of (√(1+(a/x))) + (√(1+(b/x))) → min. value of x so why x→∞ ??? it should be x→0!

$$\:{doubt}\:: \\ $$ $${we}\:{need}\:{to}\:{find}\:{max}.\:{value}\:{of} \\ $$ $$\sqrt{\mathrm{1}+\frac{{a}}{{x}}}\:+\:\sqrt{\mathrm{1}+\frac{{b}}{{x}}}\:\rightarrow\:{min}.\:{value}\:{of}\:{x} \\ $$ $${so}\:{why}\:{x}\rightarrow\infty\:???\:\:{it}\:{should}\:{be}\:{x}\rightarrow\mathrm{0}! \\ $$

Commented bytanmay.chaudhury50@gmail.com last updated on 29/Apr/18

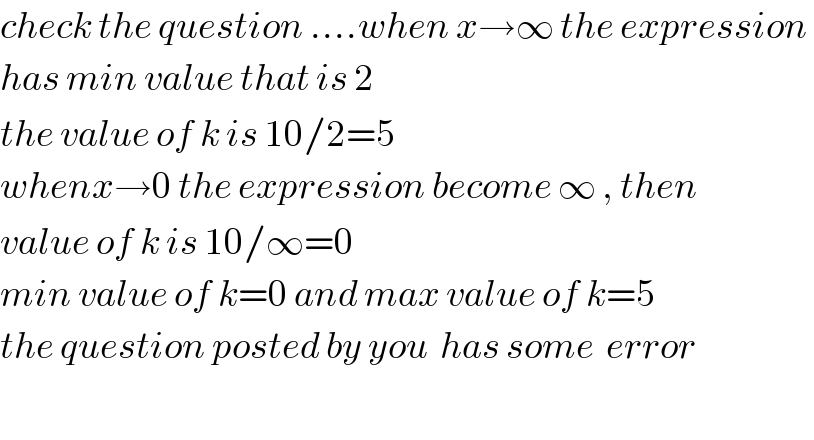
check the question ....when x→∞ the expression has min value that is 2 the value of k is 10/2=5 whenx→0 the expression become ∞ , then value of k is 10/∞=0 min value of k=0 and max value of k=5 the question posted by you has some error

$${check}\:{the}\:{question}\:....{when}\:{x}\rightarrow\infty\:{the}\:{expression}\: \\ $$ $${has}\:{min}\:{value}\:{that}\:{is}\:\mathrm{2} \\ $$ $${the}\:{value}\:{of}\:{k}\:{is}\:\mathrm{10}/\mathrm{2}=\mathrm{5} \\ $$ $${whenx}\rightarrow\mathrm{0}\:{the}\:{expression}\:{become}\:\infty\:,\:{then}\: \\ $$ $${value}\:{of}\:{k}\:{is}\:\mathrm{10}/\infty=\mathrm{0}\: \\ $$ $${min}\:{value}\:{of}\:{k}=\mathrm{0}\:{and}\:{max}\:{value}\:{of}\:{k}=\mathrm{5} \\ $$ $${the}\:{question}\:{posted}\:{by}\:{you}\:\:{has}\:{some}\:\:{error} \\ $$ $$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com