
Previous in Relation and Functions Next in Relation and Functions
Question Number 33892 by math khazana by abdo last updated on 26/Apr/18
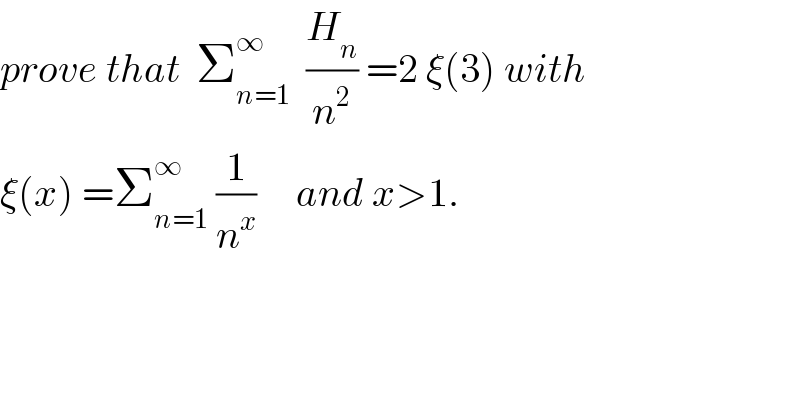
$${prove}\:{that}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{H}_{{n}} }{{n}^{\mathrm{2}} }\:=\mathrm{2}\:\xi\left(\mathrm{3}\right)\:{with} \\ $$ $$\xi\left({x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{{x}} }\:\:\:\:\:{and}\:{x}>\mathrm{1}. \\ $$
Commented bymath khazana by abdo last updated on 26/Apr/18

$${H}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:. \\ $$
