
Question Number 33789 by wath trine last updated on 24/Apr/18
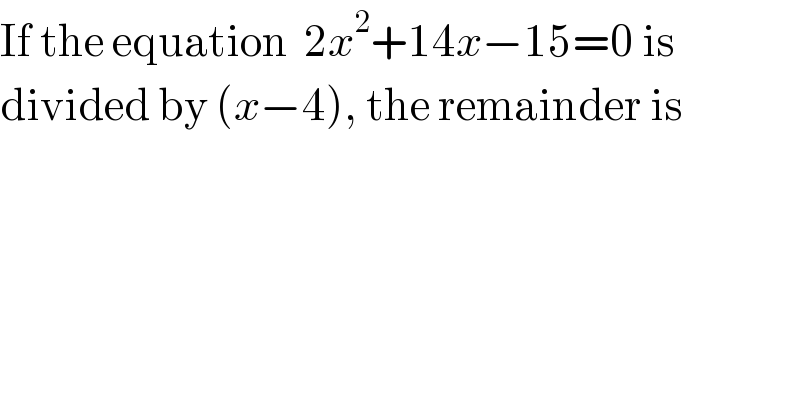
$$\mathrm{If}\:\mathrm{the}\:\mathrm{equation}\:\:\mathrm{2}{x}^{\mathrm{2}} +\mathrm{14}{x}−\mathrm{15}=\mathrm{0}\:\mathrm{is} \\ $$$$\mathrm{divided}\:\mathrm{by}\:\left({x}−\mathrm{4}\right),\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{is} \\ $$
Answered by MJS last updated on 25/Apr/18
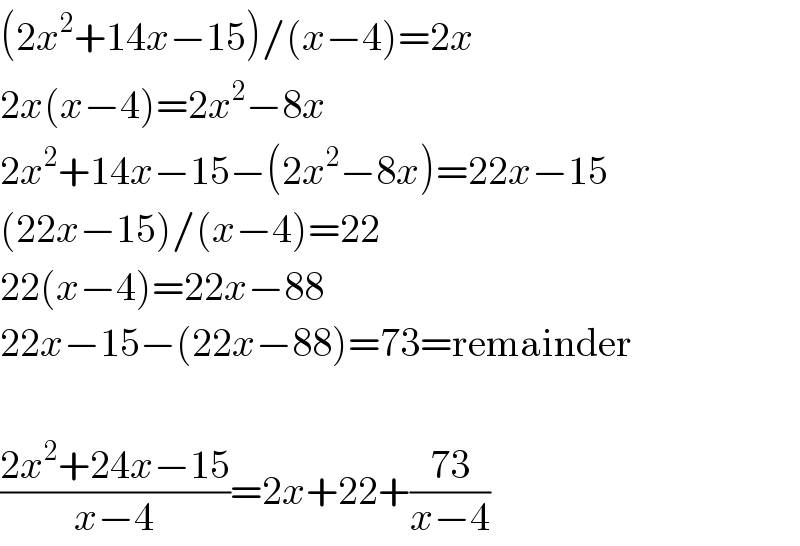
$$\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{14}{x}−\mathrm{15}\right)/\left({x}−\mathrm{4}\right)=\mathrm{2}{x} \\ $$$$\mathrm{2}{x}\left({x}−\mathrm{4}\right)=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{8}{x} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{14}{x}−\mathrm{15}−\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{8}{x}\right)=\mathrm{22}{x}−\mathrm{15} \\ $$$$\left(\mathrm{22}{x}−\mathrm{15}\right)/\left({x}−\mathrm{4}\right)=\mathrm{22} \\ $$$$\mathrm{22}\left({x}−\mathrm{4}\right)=\mathrm{22}{x}−\mathrm{88} \\ $$$$\mathrm{22}{x}−\mathrm{15}−\left(\mathrm{22}{x}−\mathrm{88}\right)=\mathrm{73}=\mathrm{remainder} \\ $$$$ \\ $$$$\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{24}{x}−\mathrm{15}}{{x}−\mathrm{4}}=\mathrm{2}{x}+\mathrm{22}+\frac{\mathrm{73}}{{x}−\mathrm{4}} \\ $$
Commented by Rasheed.Sindhi last updated on 25/Apr/18
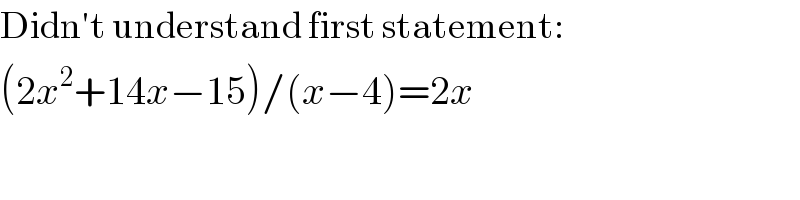
$$\mathrm{Didn}'\mathrm{t}\:\mathrm{understand}\:\mathrm{first}\:\mathrm{statement}: \\ $$$$\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{14}{x}−\mathrm{15}\right)/\left({x}−\mathrm{4}\right)=\mathrm{2}{x} \\ $$$$ \\ $$
Commented by MJS last updated on 25/Apr/18
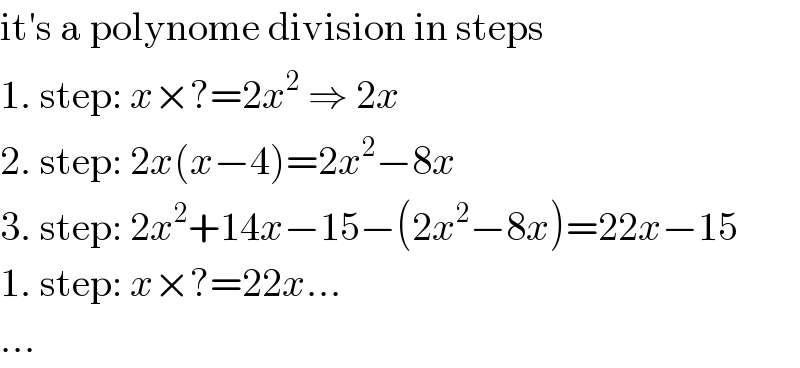
$$\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{polynome}\:\mathrm{division}\:\mathrm{in}\:\mathrm{steps} \\ $$$$\mathrm{1}.\:\mathrm{step}:\:{x}×?=\mathrm{2}{x}^{\mathrm{2}} \:\Rightarrow\:\mathrm{2}{x} \\ $$$$\mathrm{2}.\:\mathrm{step}:\:\mathrm{2}{x}\left({x}−\mathrm{4}\right)=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{8}{x} \\ $$$$\mathrm{3}.\:\mathrm{step}:\:\mathrm{2}{x}^{\mathrm{2}} +\mathrm{14}{x}−\mathrm{15}−\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{8}{x}\right)=\mathrm{22}{x}−\mathrm{15} \\ $$$$\mathrm{1}.\:\mathrm{step}:\:{x}×?=\mathrm{22}{x}... \\ $$$$... \\ $$
Commented by Rasheed.Sindhi last updated on 25/Apr/18

$$\mathbb{T}\mathrm{h}\alpha\mathrm{n}\Bbbk\mathcal{SS}{ir}! \\ $$
Commented by Joel578 last updated on 25/Apr/18

$$\mathrm{It}\:\mathrm{is}\:\mathrm{long}\:\mathrm{polynomial}\:\mathrm{division} \\ $$
Commented by Rasheed.Sindhi last updated on 25/Apr/18
$$\mathrm{Yes}\:\mathrm{sir}\:\mathrm{I}\:\mathrm{understood}. \\ $$
Answered by tawa tawa last updated on 24/Apr/18
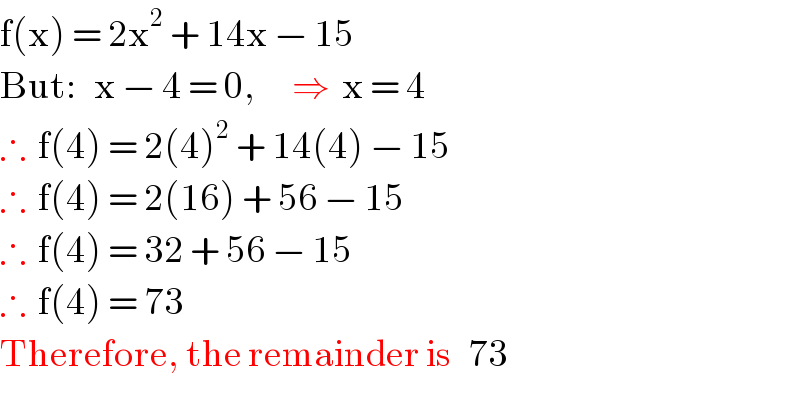
$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{2x}^{\mathrm{2}} \:+\:\mathrm{14x}\:−\:\mathrm{15} \\ $$$$\mathrm{But}:\:\:\:\mathrm{x}\:−\:\mathrm{4}\:=\:\mathrm{0},\:\:\:\:\:\:\Rightarrow\:\:\mathrm{x}\:=\:\mathrm{4} \\ $$$$\therefore\:\:\mathrm{f}\left(\mathrm{4}\right)\:=\:\mathrm{2}\left(\mathrm{4}\right)^{\mathrm{2}} \:+\:\mathrm{14}\left(\mathrm{4}\right)\:−\:\mathrm{15} \\ $$$$\therefore\:\:\mathrm{f}\left(\mathrm{4}\right)\:=\:\mathrm{2}\left(\mathrm{16}\right)\:+\:\mathrm{56}\:−\:\mathrm{15} \\ $$$$\therefore\:\:\mathrm{f}\left(\mathrm{4}\right)\:=\:\mathrm{32}\:+\:\mathrm{56}\:−\:\mathrm{15} \\ $$$$\therefore\:\:\mathrm{f}\left(\mathrm{4}\right)\:=\:\mathrm{73} \\ $$$$\mathrm{Therefore},\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\:\:\mathrm{73} \\ $$
Answered by $@ty@m last updated on 25/Apr/18

Commented by MJS last updated on 26/Apr/18
$$\mathrm{thank}\:\mathrm{you},\:\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{remember}\:\mathrm{this}... \\ $$
