
Question Number 33570 by Joel578 last updated on 19/Apr/18
![A = Σ_(n=2) ^(2017) [∫_1 ^n 2tan^(−1) x + sin^(−1) (((2x)/(1 + x^2 ))) dx] B = Π_(n=2) ^(2017) [∫_1 ^n 2tan^(−1) x + sin^(−1) (((2x)/(1 + x^2 ))) dx] A + B = ...](Q33570.png)
$${A}\:=\:\underset{{n}=\mathrm{2}} {\overset{\mathrm{2017}} {\sum}}\:\left[\underset{\mathrm{1}} {\overset{{n}} {\int}}\:\mathrm{2tan}^{−\mathrm{1}} \:{x}\:+\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}}{\mathrm{1}\:+\:{x}^{\mathrm{2}} }\right)\:{dx}\right] \\ $$$${B}\:=\:\underset{{n}=\mathrm{2}} {\overset{\mathrm{2017}} {\prod}}\:\left[\underset{\mathrm{1}} {\overset{{n}} {\int}}\:\mathrm{2tan}^{−\mathrm{1}} \:{x}\:+\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}}{\mathrm{1}\:+\:{x}^{\mathrm{2}} }\right)\:{dx}\right] \\ $$$${A}\:+\:{B}\:=\:... \\ $$
Commented by MJS last updated on 19/Apr/18

$${A}={B},\:\mathrm{yes}? \\ $$
Commented by Joel578 last updated on 20/Apr/18
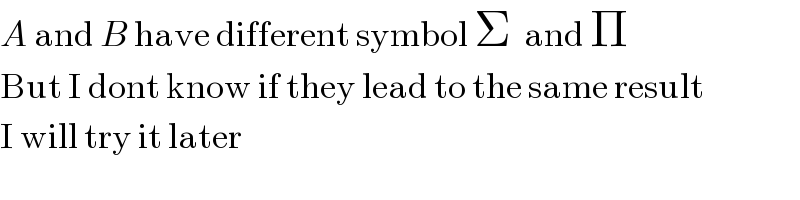
$${A}\:\mathrm{and}\:{B}\:\mathrm{have}\:\mathrm{different}\:\mathrm{symbol}\:\Sigma\:\:\mathrm{and}\:\Pi \\ $$$$\mathrm{But}\:\mathrm{I}\:\mathrm{dont}\:\mathrm{know}\:\mathrm{if}\:\mathrm{they}\:\mathrm{lead}\:\mathrm{to}\:\mathrm{the}\:\mathrm{same}\:\mathrm{result} \\ $$$$\mathrm{I}\:\mathrm{will}\:\mathrm{try}\:\mathrm{it}\:\mathrm{later} \\ $$
Commented by MJS last updated on 20/Apr/18
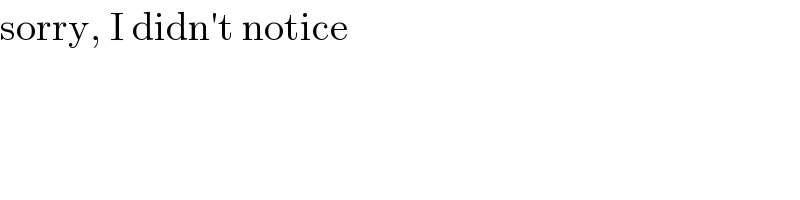
$$\mathrm{sorry},\:\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{notice} \\ $$
Answered by MJS last updated on 20/Apr/18
![θ=2tan^(−1) x ⇒ x=tan (θ/2) ∧ −π≤θ≤π sin α=((2tan (α/2))/(1+tan^2 (α/2))) ⇒ sin^(−1) ((2x)/(1+x^2 ))=θ ∧ −(π/2)≤θ≤(π/2) ⇒ { ((π+2tan^(−1) x=−sin^(−1) ((2x)/(1+x^2 )); x∈]−∞;−1])),((2tan^(−1) x=sin^(−1) ((2x)/(1+x^2 )); x∈[−1;1])),((π−2tan^(−1) x=sin^(−1) ((2x)/(1+x^2 )); x∈[1;∞[)) :} ⇒ { ((2tan^(−1) x + sin^(−1) ((2x)/(1 + x^2 ))=−π; x∈]−∞;−1])),((2tan^(−1) x + sin^(−1) ((2x)/(1 + x^2 ))4tan^(−1) x; x∈[−1;1])),((2tan^(−1) x + sin^(−1) ((2x)/(1 + x^2 ))π; x∈[1;∞[)) :} ⇒ A=Σ_(n=2) ^(2017) ∫_1 ^n πdx=Σ_(n=2) ^(2017) [πx]_1 ^n =Σ_(n=2) ^(2017) π(n−1)=Σ_(n=1) ^(2016) πn=2033136π B=Π_(n=1) ^(2016) πn=2016!π^(2016) ⇒ A+B=2033136π+2016!π^(2016)](Q33609.png)
$$\theta=\mathrm{2tan}^{−\mathrm{1}} \:{x}\:\Rightarrow\:{x}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\:\wedge\:−\pi\leqslant\theta\leqslant\pi \\ $$$$\mathrm{sin}\:\alpha=\frac{\mathrm{2tan}\:\frac{\alpha}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}}\:\Rightarrow\:\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }=\theta\:\wedge\:−\frac{\pi}{\mathrm{2}}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\:\begin{cases}{\left.\pi\left.+\mathrm{2tan}^{−\mathrm{1}} \:{x}=−\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} };\:{x}\in\right]−\infty;−\mathrm{1}\right]}\\{\mathrm{2tan}^{−\mathrm{1}} \:{x}=\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} };\:{x}\in\left[−\mathrm{1};\mathrm{1}\right]}\\{\pi−\mathrm{2tan}^{−\mathrm{1}} \:{x}=\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} };\:{x}\in\left[\mathrm{1};\infty\left[\right.\right.}\end{cases} \\ $$$$\Rightarrow\:\begin{cases}{\left.\mathrm{2}\left.\mathrm{tan}^{−\mathrm{1}} \:{x}\:+\:\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{2}{x}}{\mathrm{1}\:+\:{x}^{\mathrm{2}} }=−\pi;\:{x}\in\right]−\infty;−\mathrm{1}\right]}\\{\mathrm{2tan}^{−\mathrm{1}} \:{x}\:+\:\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{2}{x}}{\mathrm{1}\:+\:{x}^{\mathrm{2}} }\mathrm{4tan}^{−\mathrm{1}} \:{x};\:{x}\in\left[−\mathrm{1};\mathrm{1}\right]}\\{\mathrm{2tan}^{−\mathrm{1}} \:{x}\:+\:\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{2}{x}}{\mathrm{1}\:+\:{x}^{\mathrm{2}} }\pi;\:{x}\in\left[\mathrm{1};\infty\left[\right.\right.}\end{cases} \\ $$$$ \\ $$$$\Rightarrow\:{A}=\underset{{n}=\mathrm{2}} {\overset{\mathrm{2017}} {\sum}}\:\underset{\mathrm{1}} {\overset{{n}} {\int}}\pi{dx}=\underset{{n}=\mathrm{2}} {\overset{\mathrm{2017}} {\sum}}\:\left[\pi{x}\right]_{\mathrm{1}} ^{{n}} =\underset{{n}=\mathrm{2}} {\overset{\mathrm{2017}} {\sum}}\:\pi\left({n}−\mathrm{1}\right)=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2016}} {\sum}}\pi{n}=\mathrm{2033136}\pi \\ $$$$\:\:\:\:\:\:{B}=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2016}} {\prod}}\:\pi{n}=\mathrm{2016}!\pi^{\mathrm{2016}} \\ $$$$\Rightarrow\:{A}+{B}=\mathrm{2033136}\pi+\mathrm{2016}!\pi^{\mathrm{2016}} \\ $$
