Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 33569 by Joel578 last updated on 19/Apr/18

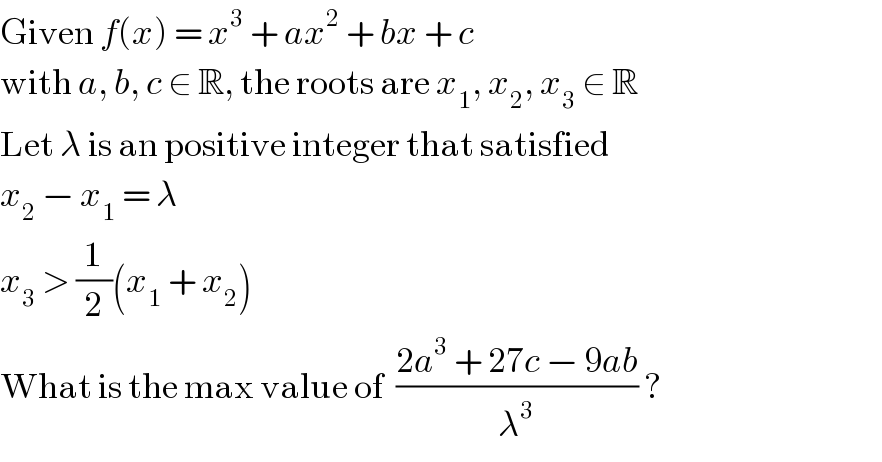
Given f(x) = x^3 + ax^2 + bx + c with a, b, c ∈ R, the roots are x_1 , x_2 , x_3 ∈ R Let λ is an positive integer that satisfied x_2 − x_1 = λ x_3 > (1/2)(x_1 + x_2 ) What is the max value of ((2a^3 + 27c − 9ab)/λ^3 ) ?

$$\mathrm{Given}\:{f}\left({x}\right)\:=\:{x}^{\mathrm{3}} \:+\:{ax}^{\mathrm{2}} \:+\:{bx}\:+\:{c} \\ $$ $$\mathrm{with}\:{a},\:{b},\:{c}\:\in\:\mathbb{R},\:\mathrm{the}\:\mathrm{roots}\:\mathrm{are}\:{x}_{\mathrm{1}} ,\:{x}_{\mathrm{2}} ,\:{x}_{\mathrm{3}} \:\in\:\mathbb{R} \\ $$ $$\mathrm{Let}\:\lambda\:\mathrm{is}\:\mathrm{an}\:\mathrm{positive}\:\mathrm{integer}\:\mathrm{that}\:\mathrm{satisfied} \\ $$ $${x}_{\mathrm{2}} \:−\:{x}_{\mathrm{1}} \:=\:\lambda \\ $$ $${x}_{\mathrm{3}} \:>\:\frac{\mathrm{1}}{\mathrm{2}}\left({x}_{\mathrm{1}} \:+\:{x}_{\mathrm{2}} \right) \\ $$ $$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{max}\:\mathrm{value}\:\mathrm{of}\:\:\frac{\mathrm{2}{a}^{\mathrm{3}} \:+\:\mathrm{27}{c}\:−\:\mathrm{9}{ab}}{\lambda^{\mathrm{3}} }\:? \\ $$

Answered by MJS last updated on 20/Apr/18

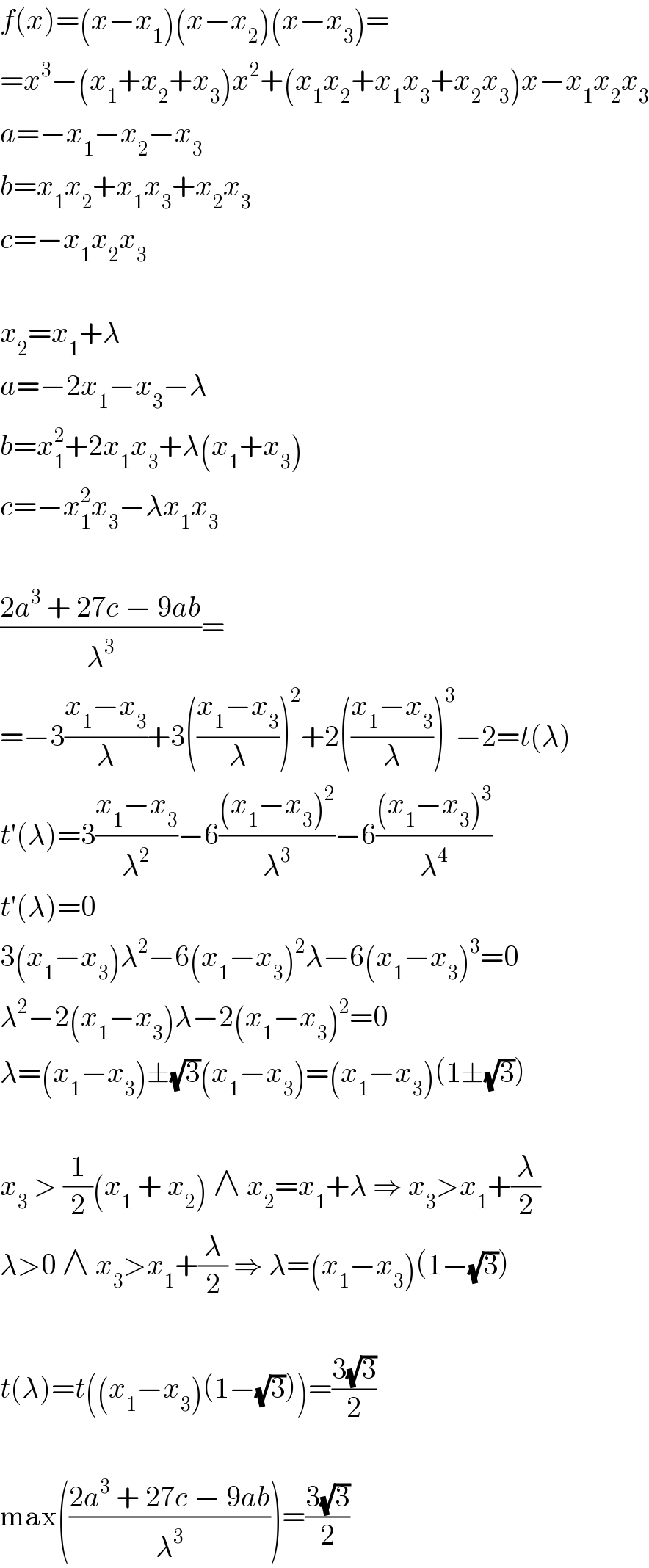
f(x)=(x−x_1 )(x−x_2 )(x−x_3 )= =x^3 −(x_1 +x_2 +x_3 )x^2 +(x_1 x_2 +x_1 x_3 +x_2 x_3 )x−x_1 x_2 x_3 a=−x_1 −x_2 −x_3 b=x_1 x_2 +x_1 x_3 +x_2 x_3 c=−x_1 x_2 x_3 x_2 =x_1 +λ a=−2x_1 −x_3 −λ b=x_1 ^2 +2x_1 x_3 +λ(x_1 +x_3 ) c=−x_1 ^2 x_3 −λx_1 x_3 ((2a^3 + 27c − 9ab)/λ^3 )= =−3((x_1 −x_3 )/λ)+3(((x_1 −x_3 )/λ))^2 +2(((x_1 −x_3 )/λ))^3 −2=t(λ) t′(λ)=3((x_1 −x_3 )/λ^2 )−6(((x_1 −x_3 )^2 )/λ^3 )−6(((x_1 −x_3 )^3 )/λ^4 ) t′(λ)=0 3(x_1 −x_3 )λ^2 −6(x_1 −x_3 )^2 λ−6(x_1 −x_3 )^3 =0 λ^2 −2(x_1 −x_3 )λ−2(x_1 −x_3 )^2 =0 λ=(x_1 −x_3 )±(√3)(x_1 −x_3 )=(x_1 −x_3 )(1±(√3)) x_3 > (1/2)(x_1 + x_2 ) ∧ x_2 =x_1 +λ ⇒ x_3 >x_1 +(λ/2) λ>0 ∧ x_3 >x_1 +(λ/2) ⇒ λ=(x_1 −x_3 )(1−(√3)) t(λ)=t((x_1 −x_3 )(1−(√3)))=((3(√3))/2) max(((2a^3 + 27c − 9ab)/λ^3 ))=((3(√3))/2)

$${f}\left({x}\right)=\left({x}−{x}_{\mathrm{1}} \right)\left({x}−{x}_{\mathrm{2}} \right)\left({x}−{x}_{\mathrm{3}} \right)= \\ $$ $$={x}^{\mathrm{3}} −\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} \right){x}^{\mathrm{2}} +\left({x}_{\mathrm{1}} {x}_{\mathrm{2}} +{x}_{\mathrm{1}} {x}_{\mathrm{3}} +{x}_{\mathrm{2}} {x}_{\mathrm{3}} \right){x}−{x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} \\ $$ $${a}=−{x}_{\mathrm{1}} −{x}_{\mathrm{2}} −{x}_{\mathrm{3}} \\ $$ $${b}={x}_{\mathrm{1}} {x}_{\mathrm{2}} +{x}_{\mathrm{1}} {x}_{\mathrm{3}} +{x}_{\mathrm{2}} {x}_{\mathrm{3}} \\ $$ $${c}=−{x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} \\ $$ $$ \\ $$ $${x}_{\mathrm{2}} ={x}_{\mathrm{1}} +\lambda \\ $$ $${a}=−\mathrm{2}{x}_{\mathrm{1}} −{x}_{\mathrm{3}} −\lambda \\ $$ $${b}={x}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{2}{x}_{\mathrm{1}} {x}_{\mathrm{3}} +\lambda\left({x}_{\mathrm{1}} +{x}_{\mathrm{3}} \right) \\ $$ $${c}=−{x}_{\mathrm{1}} ^{\mathrm{2}} {x}_{\mathrm{3}} −\lambda{x}_{\mathrm{1}} {x}_{\mathrm{3}} \\ $$ $$ \\ $$ $$\frac{\mathrm{2}{a}^{\mathrm{3}} \:+\:\mathrm{27}{c}\:−\:\mathrm{9}{ab}}{\lambda^{\mathrm{3}} }= \\ $$ $$=−\mathrm{3}\frac{{x}_{\mathrm{1}} −{x}_{\mathrm{3}} }{\lambda}+\mathrm{3}\left(\frac{{x}_{\mathrm{1}} −{x}_{\mathrm{3}} }{\lambda}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{{x}_{\mathrm{1}} −{x}_{\mathrm{3}} }{\lambda}\right)^{\mathrm{3}} −\mathrm{2}={t}\left(\lambda\right) \\ $$ $${t}'\left(\lambda\right)=\mathrm{3}\frac{{x}_{\mathrm{1}} −{x}_{\mathrm{3}} }{\lambda^{\mathrm{2}} }−\mathrm{6}\frac{\left({x}_{\mathrm{1}} −{x}_{\mathrm{3}} \right)^{\mathrm{2}} }{\lambda^{\mathrm{3}} }−\mathrm{6}\frac{\left({x}_{\mathrm{1}} −{x}_{\mathrm{3}} \right)^{\mathrm{3}} }{\lambda^{\mathrm{4}} } \\ $$ $${t}'\left(\lambda\right)=\mathrm{0} \\ $$ $$\mathrm{3}\left({x}_{\mathrm{1}} −{x}_{\mathrm{3}} \right)\lambda^{\mathrm{2}} −\mathrm{6}\left({x}_{\mathrm{1}} −{x}_{\mathrm{3}} \right)^{\mathrm{2}} \lambda−\mathrm{6}\left({x}_{\mathrm{1}} −{x}_{\mathrm{3}} \right)^{\mathrm{3}} =\mathrm{0} \\ $$ $$\lambda^{\mathrm{2}} −\mathrm{2}\left({x}_{\mathrm{1}} −{x}_{\mathrm{3}} \right)\lambda−\mathrm{2}\left({x}_{\mathrm{1}} −{x}_{\mathrm{3}} \right)^{\mathrm{2}} =\mathrm{0} \\ $$ $$\lambda=\left({x}_{\mathrm{1}} −{x}_{\mathrm{3}} \right)\pm\sqrt{\mathrm{3}}\left({x}_{\mathrm{1}} −{x}_{\mathrm{3}} \right)=\left({x}_{\mathrm{1}} −{x}_{\mathrm{3}} \right)\left(\mathrm{1}\pm\sqrt{\mathrm{3}}\right) \\ $$ $$ \\ $$ $${x}_{\mathrm{3}} \:>\:\frac{\mathrm{1}}{\mathrm{2}}\left({x}_{\mathrm{1}} \:+\:{x}_{\mathrm{2}} \right)\:\wedge\:{x}_{\mathrm{2}} ={x}_{\mathrm{1}} +\lambda\:\Rightarrow\:{x}_{\mathrm{3}} >{x}_{\mathrm{1}} +\frac{\lambda}{\mathrm{2}} \\ $$ $$\lambda>\mathrm{0}\:\wedge\:{x}_{\mathrm{3}} >{x}_{\mathrm{1}} +\frac{\lambda}{\mathrm{2}}\:\Rightarrow\:\lambda=\left({x}_{\mathrm{1}} −{x}_{\mathrm{3}} \right)\left(\mathrm{1}−\sqrt{\mathrm{3}}\right) \\ $$ $$ \\ $$ $${t}\left(\lambda\right)={t}\left(\left({x}_{\mathrm{1}} −{x}_{\mathrm{3}} \right)\left(\mathrm{1}−\sqrt{\mathrm{3}}\right)\right)=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$ $$ \\ $$ $$\mathrm{max}\left(\frac{\mathrm{2}{a}^{\mathrm{3}} \:+\:\mathrm{27}{c}\:−\:\mathrm{9}{ab}}{\lambda^{\mathrm{3}} }\right)=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$

Commented byJoel578 last updated on 20/Apr/18

thank you very much

$${thank}\:{you}\:{very}\:{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com