
Previous in Relation and Functions Next in Relation and Functions
Question Number 33336 by prof Abdo imad last updated on 14/Apr/18
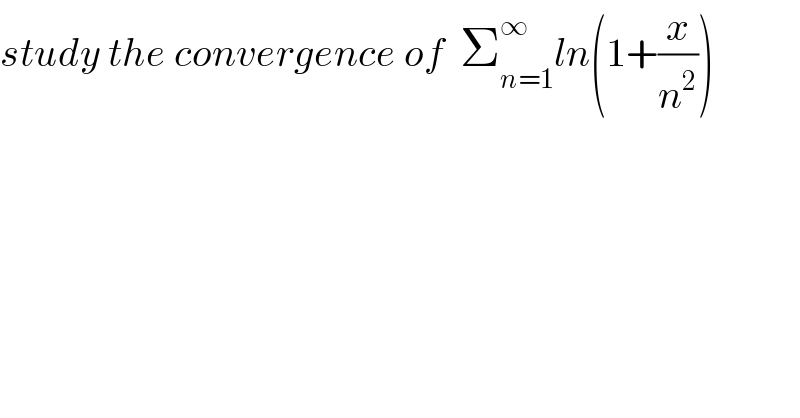
$${study}\:{the}\:{convergence}\:{of}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} {ln}\left(\mathrm{1}+\frac{{x}}{{n}^{\mathrm{2}} }\right) \\ $$
Commented by prof Abdo imad last updated on 25/Apr/18
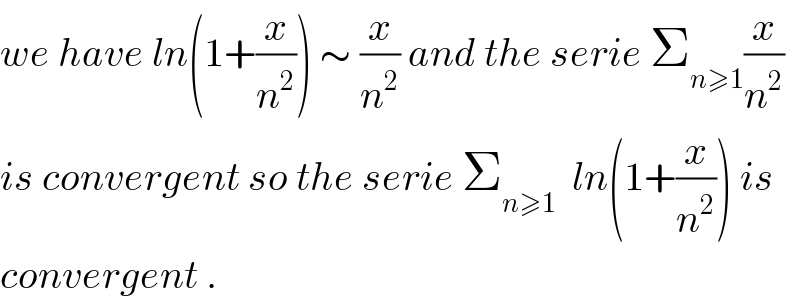
$${we}\:{have}\:{ln}\left(\mathrm{1}+\frac{{x}}{{n}^{\mathrm{2}} }\right)\:\sim\:\frac{{x}}{{n}^{\mathrm{2}} }\:{and}\:{the}\:{serie}\:\sum_{{n}\geqslant\mathrm{1}} \frac{{x}}{{n}^{\mathrm{2}} } \\ $$$${is}\:{convergent}\:{so}\:{the}\:{serie}\:\sum_{{n}\geqslant\mathrm{1}} \:\:{ln}\left(\mathrm{1}+\frac{{x}}{{n}^{\mathrm{2}} }\right)\:{is} \\ $$$${convergent}\:. \\ $$
