
Question Number 33322 by Rio Mike last updated on 15/Apr/18
![a) px^2 + 3x + q=0 has roots [((α+β)/(αβ))]× αβ find p and q if x^2 − 7x + 4 = 0 with real and distinct roots has same roots.. b)if α and β are roots of x^2 + kx +2k+8=0. a) find k if one root is twice the other.](Q33322.png)
$$\left.{a}\right)\:{px}^{\mathrm{2}} +\:\mathrm{3}{x}\:+\:{q}=\mathrm{0}\:{has}\:{roots}\: \\ $$$$\:\:\left[\frac{\alpha+\beta}{\alpha\beta}\right]×\:\alpha\beta \\ $$$${find}\:{p}\:{and}\:{q}\:{if}\: \\ $$$$\:\:{x}^{\mathrm{2}} −\:\mathrm{7}{x}\:+\:\mathrm{4}\:=\:\mathrm{0}\:{with}\:{real}\:{and}\: \\ $$$${distinct}\:{roots}\:{has}\:{same}\:{roots}.. \\ $$$$\left.{b}\right){if}\:\alpha\:{and}\:\beta\:{are}\:{roots}\:{of}\: \\ $$$$\:{x}^{\mathrm{2}} +\:{kx}\:+\mathrm{2}{k}+\mathrm{8}=\mathrm{0}. \\ $$$$\left.{a}\right)\:{find}\:{k}\:{if}\:{one}\:{root}\:{is}\:{twice}\:{the}\:{other}. \\ $$
Commented by Rio Mike last updated on 15/Apr/18
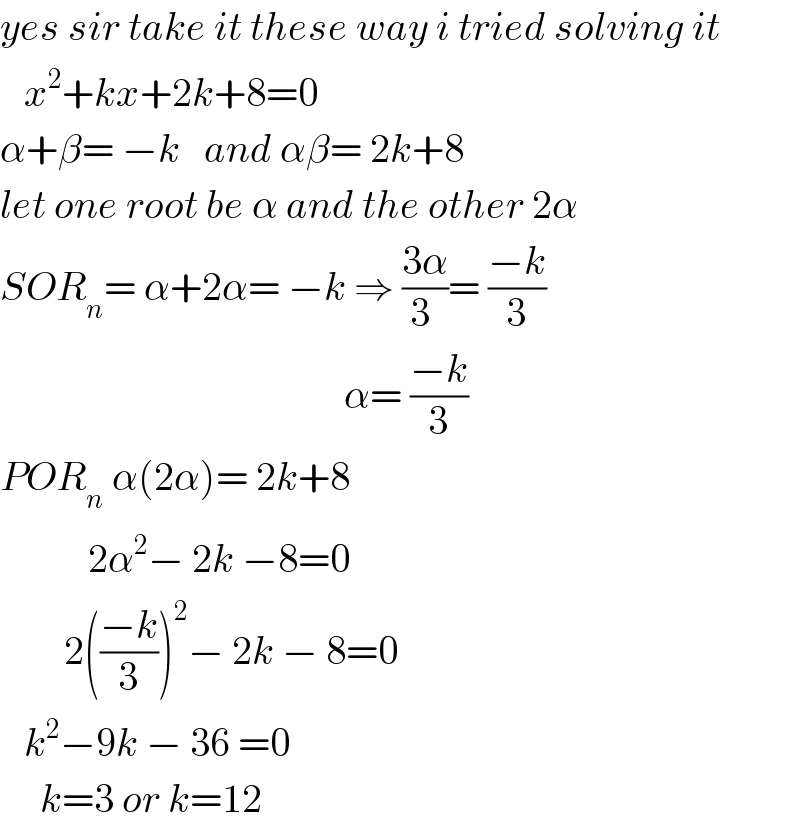
$${yes}\:{sir}\:{take}\:{it}\:{these}\:{way}\:{i}\:{tried}\:{solving}\:{it} \\ $$$$\:\:\:{x}^{\mathrm{2}} +{kx}+\mathrm{2}{k}+\mathrm{8}=\mathrm{0} \\ $$$$\alpha+\beta=\:−{k}\:\:\:{and}\:\alpha\beta=\:\mathrm{2}{k}+\mathrm{8} \\ $$$${let}\:{one}\:{root}\:{be}\:\alpha\:{and}\:{the}\:{other}\:\mathrm{2}\alpha \\ $$$${SOR}_{{n}} =\:\alpha+\mathrm{2}\alpha=\:−{k}\:\Rightarrow\:\frac{\mathrm{3}\alpha}{\mathrm{3}\:}=\:\frac{−{k}}{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\alpha=\:\frac{−{k}}{\mathrm{3}} \\ $$$${POR}_{{n}} \:\alpha\left(\mathrm{2}\alpha\right)=\:\mathrm{2}{k}+\mathrm{8}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\alpha^{\mathrm{2}} −\:\mathrm{2}{k}\:−\mathrm{8}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}\left(\frac{−{k}}{\mathrm{3}}\right)^{\mathrm{2}} −\:\mathrm{2}{k}\:−\:\mathrm{8}=\mathrm{0} \\ $$$$\:\:\:{k}^{\mathrm{2}} −\mathrm{9}{k}\:−\:\mathrm{36}\:=\mathrm{0} \\ $$$$\:\:\:\:\:{k}=\mathrm{3}\:{or}\:{k}=\mathrm{12} \\ $$
Commented by MJS last updated on 15/Apr/18
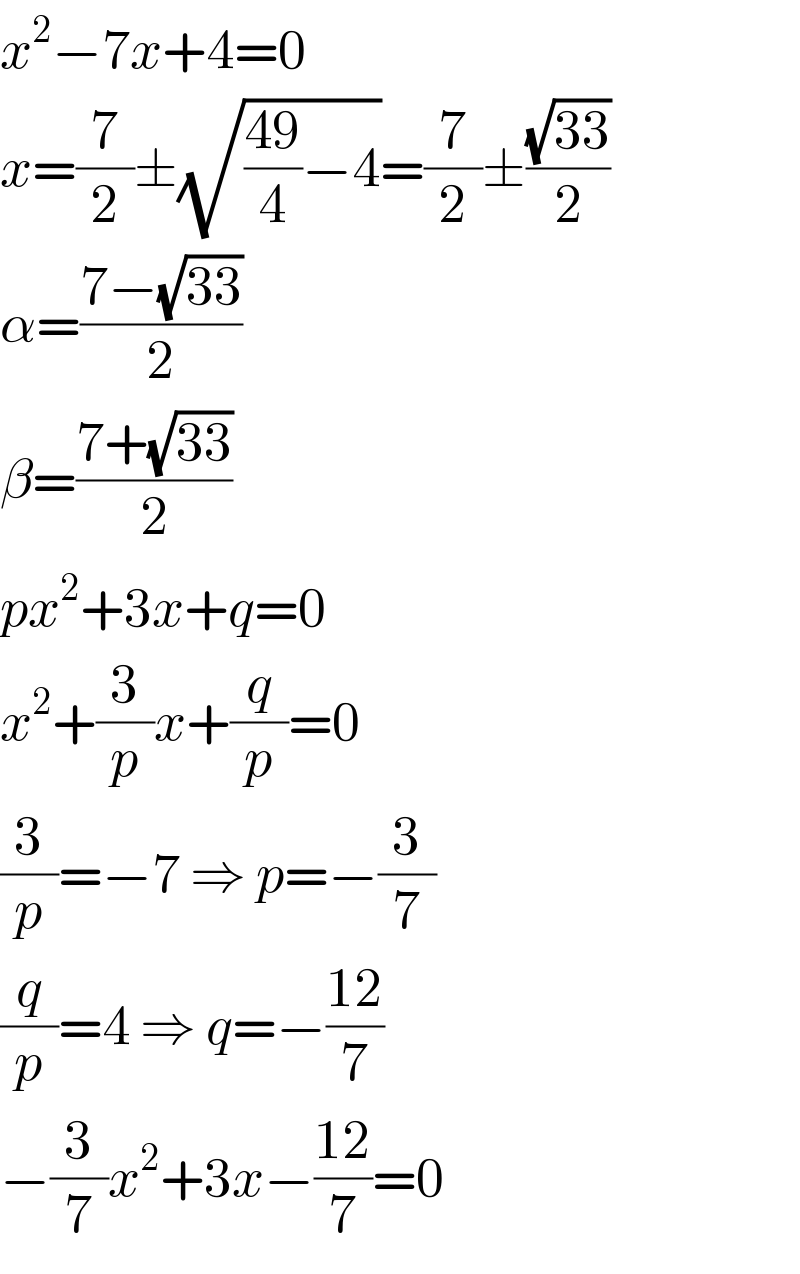
$${x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{4}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{7}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{49}}{\mathrm{4}}−\mathrm{4}}=\frac{\mathrm{7}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{33}}}{\mathrm{2}} \\ $$$$\alpha=\frac{\mathrm{7}−\sqrt{\mathrm{33}}}{\mathrm{2}} \\ $$$$\beta=\frac{\mathrm{7}+\sqrt{\mathrm{33}}}{\mathrm{2}} \\ $$$${px}^{\mathrm{2}} +\mathrm{3}{x}+{q}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{3}}{{p}}{x}+\frac{{q}}{{p}}=\mathrm{0} \\ $$$$\frac{\mathrm{3}}{{p}}=−\mathrm{7}\:\Rightarrow\:{p}=−\frac{\mathrm{3}}{\mathrm{7}} \\ $$$$\frac{{q}}{{p}}=\mathrm{4}\:\Rightarrow\:{q}=−\frac{\mathrm{12}}{\mathrm{7}} \\ $$$$−\frac{\mathrm{3}}{\mathrm{7}}{x}^{\mathrm{2}} +\mathrm{3}{x}−\frac{\mathrm{12}}{\mathrm{7}}=\mathrm{0} \\ $$
Commented by MJS last updated on 15/Apr/18

$$\mathrm{sorry}\:\mathrm{somehow}\:\mathrm{I}\:\mathrm{thought}\:\mathrm{it}\:\mathrm{was} \\ $$$$\left.{x}^{\mathrm{3}} ...\:\mathrm{I}\:\mathrm{might}\:\mathrm{need}\:\mathrm{new}\:\mathrm{glasses}\:;−\right) \\ $$$$\mathrm{anyway}\:\mathrm{your}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{right} \\ $$
Commented by Rasheed.Sindhi last updated on 16/Apr/18
![What is the use of [((α+β)/(αβ))]× αβ ?](Q33448.png)
$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{use}\:\mathrm{of}\:\left[\frac{\alpha+\beta}{\alpha\beta}\right]×\:\alpha\beta\:? \\ $$
