
Question Number 3324 by prakash jain last updated on 10/Dec/15
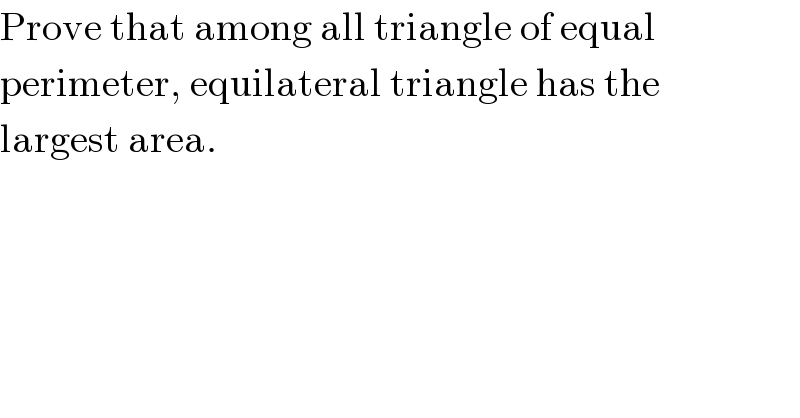
$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{among}\:\mathrm{all}\:\mathrm{triangle}\:\mathrm{of}\:\mathrm{equal} \\ $$$$\mathrm{perimeter},\:\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{has}\:\mathrm{the} \\ $$$$\mathrm{largest}\:\mathrm{area}. \\ $$
Commented by 123456 last updated on 10/Dec/15
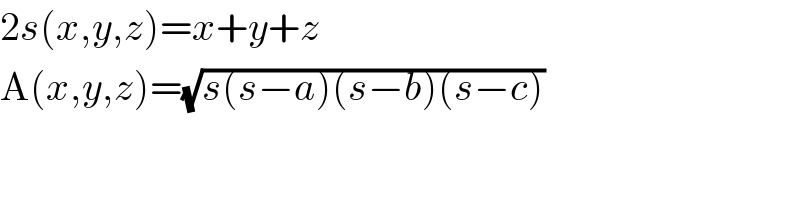
$$\mathrm{2}{s}\left({x},{y},{z}\right)={x}+{y}+{z} \\ $$$$\mathrm{A}\left({x},{y},{z}\right)=\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$
Commented by Rasheed Soomro last updated on 11/Dec/15

$${Let}\:{x},{x}+{l}\:\:{and}\:\:{x}+{l}+{m}\:\:{are}\:{measures}\:{of}\:\:{three}\:{sides} \\ $$$${where}\:{l},{m}\geqslant\mathrm{0} \\ $$$$\:\:\:\:\:\:{Perimeter}=\mathrm{3}{x}+\mathrm{2}{l}+{m} \\ $$$$\:\:\:\:\:\:\:\:\:{S}=\frac{\mathrm{3}{x}+\mathrm{2}{l}+{m}}{\mathrm{2}} \\ $$$$\mathcal{I}{n}\:\mathcal{E}{quilateral}\:{triangle}\:{S}=\frac{\mathrm{3}{x}}{\mathrm{2}}\:\:{for}\:{l},{m}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{A}_{\bigtriangleup} =\sqrt{\frac{\mathrm{3}{x}}{\mathrm{2}}\left(\frac{\mathrm{3}{x}}{\mathrm{2}}−{x}\right)^{\mathrm{3}} }=\sqrt{\frac{\mathrm{3}{x}}{\mathrm{2}}×\frac{{x}^{\mathrm{3}} }{\mathrm{2}^{\mathrm{3}} }} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\frac{\mathrm{3}{x}^{\mathrm{4}} }{\mathrm{2}^{\mathrm{4}} }}=\frac{\sqrt{\mathrm{3}}\:{x}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${As}\:{S}\:{is}\:{constant}\:\left({because}\:{perimeter}\:{is}\:{constant}\right. \\ $$$${Hence}\:{for}\:{any}\:{triangle}\:{S} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{S}=\frac{\mathrm{3}{x}}{\mathrm{2}} \\ $$$${Area}\:{of}\:{any}\:{triangle}\: \\ $$$$\:\:{A}=\sqrt{\frac{\mathrm{3}{x}}{\mathrm{2}}\left(\frac{\mathrm{3}{x}}{\mathrm{2}}−{x}\right)\left(\frac{\mathrm{3}{x}}{\mathrm{2}}−{x}−{l}\right)\left(\frac{\mathrm{3}{x}}{\mathrm{2}}−{x}−{l}−{m}\right)} \\ $$$$\:\:\:\:\:\:\:=\sqrt{\frac{\mathrm{3}{x}}{\mathrm{2}}×\frac{{x}}{\mathrm{2}}×\frac{{x}−\mathrm{2}{l}}{\mathrm{2}}×\frac{{x}−\mathrm{2}{l}−\mathrm{2}{m}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:=\frac{\sqrt{\mathrm{3}{x}^{\mathrm{2}} \left({x}−\mathrm{2}{l}\right)\left({x}−\mathrm{2}{l}−\mathrm{2}{m}\right)}}{\mathrm{4}} \\ $$$${We}\:{have}\:{to}\:{prove}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{A}_{\bigtriangleup} \geqslant{A} \\ $$$$\frac{\sqrt{\mathrm{3}}\:{x}^{\mathrm{2}} }{\mathrm{4}}\geqslant\frac{\sqrt{\mathrm{3}{x}^{\mathrm{2}} \left({x}−\mathrm{2}{l}\right)\left({x}−\mathrm{2}{l}−\mathrm{2}{m}\right)}}{\mathrm{4}}\:\:{for}\:{l},{m}\geqslant\mathrm{0} \\ $$$${C}^{\mathcal{ONTINUE}} \\ $$
Commented by prakash jain last updated on 11/Dec/15

$$\mathrm{From}\:\mathrm{your}\:\mathrm{derivation} \\ $$$$\mathrm{In}\:\mathrm{your}\:\mathrm{formula}\:\mathrm{for}\:\mathrm{area} \\ $$$${a}={x},\:{b}={x}−{l},\:{c}={x}−{l}−{m} \\ $$$${how}\:{s}=\frac{\mathrm{3}{x}}{\mathrm{2}} \\ $$
Commented by Rasheed Soomro last updated on 12/Dec/15

$${For}\:{equilateral}\:{triangle}\:{of}\:{side}\:{x}\:\:{S}=\frac{\mathrm{3}{x}}{\mathrm{2}} \\ $$$${and}\:{I}\:{have}\:{used}\:{this}\:{also}\:\:{in}\:{case}\:{of}\:{common} \\ $$$${triangle},{because}\:{the}\:{perimeter}\:{is}\:{constant}. \\ $$$$\mathcal{B}{ut}\:{now}\:{I}\:{have}\:{changed}\:{my}\:{mind}.\:{I}\:{am}\:{working} \\ $$$${on}\:{different}\:{way}.\:{Pl}\:{see}\:{my}\:{answer}\:{below}. \\ $$$${I}\:{am}\:{always}\:\:\boldsymbol{\mathrm{thankful}}\:{to}\:{you}\:{for}\:{guidance}. \\ $$
Answered by Rasheed Soomro last updated on 13/Dec/15

$$\mathcal{A}{rea}\:\:{of}\:\:\mathcal{C}{ommon}\:\mathcal{T}{riangle} \\ $$$${Let}\:{the}\:{measures}\:{of}\:{sides}\:{of}\:\:{a}\:{common}\:{triangle}\:{are} \\ $$$${x},{y},{z}\: \\ $$$$\mathcal{A}{rea}\left({A}\right)\:{will}\:{be} \\ $$$$\:\:\:\:\:\:{A}=\sqrt{{S}\left({S}−{x}\right)\left({S}−{y}\right)\left({S}−{x}\right)}\:\:\:\:;\:\:{S}=\frac{\mathrm{1}}{\mathrm{2}}\left({x}+{y}+{z}\right) \\ $$$$\:\:\:\:=\sqrt{\frac{{x}+{y}+{z}}{\mathrm{2}}\left(\frac{{x}+{y}+{z}}{\mathrm{2}}−{x}\right)\left(\frac{{x}+{y}+{z}}{\mathrm{2}}−{y}\right)\left(\frac{{x}+{y}+{z}}{\mathrm{2}}−{z}\right)} \\ $$$$\:\:\:\:=\sqrt{\left(\frac{{x}+{y}+{z}}{\mathrm{2}}\right)\left(\frac{{x}+{y}+{z}−\mathrm{2}{x}}{\mathrm{2}}\right)\left(\frac{{x}+{y}+{z}−\mathrm{2}{y}}{\mathrm{2}}\right)\left(\frac{{x}+{y}+{z}−\mathrm{2}{z}}{\mathrm{2}}\right)} \\ $$$$\:\:\:\:=\sqrt{\left(\frac{{x}+{y}+{z}}{\mathrm{2}}\right)\left(\frac{−{x}+{y}+{z}}{\mathrm{2}}\right)\left(\frac{{x}−{y}+{z}}{\mathrm{2}}\right)\left(\frac{{x}+{y}−{z}}{\mathrm{2}}\right)} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\left({x}+{y}+{z}\right)\left(−{x}+{y}+{z}\right)\left({x}−{y}+{z}\right)\left({x}+{y}−{z}\right)} \\ $$$$\mathcal{A}{rea}\:\:{of}\:\:\mathcal{E}{quilateral}\:\mathcal{T}{riangle} \\ $$$$\therefore\:{Every}\:{side}\:\:{of}\:\:{of}\:{an}\:{equilateral}\:{triangle}\:{having}\: \\ $$$${same}\:{perimeter}\:\left({x}+{y}+{z}\right)\:{is}\:\:\frac{{x}+{y}+{z}}{\mathrm{3}} \\ $$$$\:\therefore\:\:\:{A}_{\bigtriangleup} =\sqrt{{S}\left({S}−\:\frac{{x}+{y}+{z}}{\mathrm{3}}\right)^{\mathrm{3}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\frac{{x}+{y}+{z}}{\mathrm{2}}×\left(\frac{{x}+{y}+{z}}{\mathrm{2}}−\frac{{x}+{y}+{z}}{\mathrm{3}}\right)^{\mathrm{3}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\frac{{x}+{y}+{z}}{\mathrm{2}}×\left(\frac{\mathrm{3}{x}+\mathrm{3}{y}+\mathrm{3}{z}−\mathrm{2}{x}−\mathrm{2}{y}−\mathrm{2}{z}}{\mathrm{6}}\right)^{\mathrm{3}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\frac{{x}+{y}+{z}}{\mathrm{2}}×\left(\frac{{x}+{y}+{z}}{\mathrm{6}}\right)^{\mathrm{3}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\frac{\left({x}+{y}+{z}\right)^{\mathrm{4}} }{\mathrm{2}^{\mathrm{4}} ×\mathrm{3}^{\mathrm{2}} ×\mathrm{3}}}=\frac{\left({x}+{y}+{z}\right)^{\mathrm{2}} }{\mathrm{12}}×\frac{\mathrm{1}}{\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:\:{A}_{\bigtriangleup} =\frac{\left({x}+{y}+{z}\right)^{\mathrm{2}} }{\mathrm{12}\sqrt{\mathrm{3}}} \\ $$$$−−−−−<><><><>−−−−− \\ $$$${Now}\:{we}\:{have}\:{to}\:{prove}: \\ $$$${A}_{\bigtriangleup} \geqslant{A} \\ $$$$\:\:\frac{\left({x}+{y}+{z}\right)^{\mathrm{2}} }{\mathrm{12}\sqrt{\mathrm{3}}}\geqslant\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\left({x}+{y}+{z}\right)\left(−{x}+{y}+{z}\right)\left({x}−{y}+{z}\right)\left({x}+{y}−{z}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{for}\:{x},{y},{z}>\mathrm{0} \\ $$$$\Rightarrow\frac{\left({x}+{y}+{z}\right)^{\mathrm{2}} }{\mathrm{3}\sqrt{\mathrm{3}}}\geqslant\sqrt{\left({x}+{y}+{z}\right)\left(−{x}+{y}+{z}\right)\left({x}−{y}+{z}\right)\left({x}+{y}−{z}\right)} \\ $$$$\boldsymbol{\mathrm{Yozzi}}'{s}\:\boldsymbol{\mathrm{contribution}}: \\ $$$${Yozzi}\:{has}\:{proved}\:{that} \\ $$$$\Rightarrow\frac{\left({x}+{y}+{z}\right)^{\mathrm{2}} }{\mathrm{4}}\geqslant\sqrt{\left({x}+{y}+{z}\right)\left(−{x}+{y}+{z}\right)\left({x}−{y}+{z}\right)\left({x}+{y}−{z}\right)} \\ $$$$\left({See}\:{answer}\:\:{by}\:{Yozzi}.\:{An}\:{approach}\:{I}\:{can}'{t}\:{even}\right. \\ $$$$\left.{think}\:{of}!\right) \\ $$$${Now}\:{since}\:\mathrm{4}<\mathrm{3}\sqrt{\mathrm{3}} \\ $$$$\therefore\:\:\:\:\frac{\left({x}+{y}+{z}\right)^{\mathrm{2}} }{\mathrm{3}\sqrt{\mathrm{3}}}\geqslant\sqrt{\left({x}+{y}+{z}\right)\left(−{x}+{y}+{z}\right)\left({x}−{y}+{z}\right)\left({x}+{y}−{z}\right)} \\ $$$$\therefore\:{A}_{\bigtriangleup} \geqslant{A} \\ $$$${QED} \\ $$
Commented by Rasheed Soomro last updated on 14/Dec/15

$$\frac{\left({x}+{y}+{z}\right)^{\mathrm{2}} }{\mathrm{4}}\geqslant\sqrt{\underset{{r}=\mathrm{1}} {\overset{\mathrm{4}} {\prod}}{a}_{{r}} } \\ $$$${it}\:{cannot}\:{solely}\:{lead}\:{one}\:{to}\:{safely}\:{stating} \\ $$$${that}\:\frac{\left({x}+{y}+{z}\right)^{\mathrm{2}} }{\mathrm{3}\sqrt{\mathrm{3}}}\geqslant\sqrt{\underset{{r}=\mathrm{1}} {\overset{\mathrm{4}} {\prod}}{a}_{{r}} }\:. \\ $$$$\vdots \\ $$$${Why}\:{transitive}\:{property}\:{of}\:{inequality}\:{doesn}'{t} \\ $$$${help}\:? \\ $$$${If}\:{we}\:{have}\:{to}\:{prove}\:{that}\:{A}>{B}\:\:{and}\:\:{we}\:{have} \\ $$$${by}\:{some}\:{way}\:\frac{{A}}{\mathrm{2}}>{B} \\ $$$$\frac{{A}}{\mathrm{2}}>{B}\:\Rightarrow\:{A}>{B}\:? \\ $$$$ \\ $$
Commented by Yozzii last updated on 13/Dec/15

$${If}\:\mathrm{4}<\mathrm{3}\sqrt{\mathrm{3}}\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}>\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{3}}}\Rightarrow\frac{\left({x}+{y}+{z}\right)^{\mathrm{2}} }{\mathrm{4}}>\frac{\left({x}+{y}+{z}\right)^{\mathrm{2}} }{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$${Now},\:{we}\:{really}\:{weren}'{t}\:{given}\:{that} \\ $$$${A}_{\bigtriangleup} \geqslant{A}.\:{Even}\:{if}\:{we}\:{were}\:{to}\:{check}\: \\ $$$${that}\:{this}\:{is}\:{the}\:{case},\:{we}\:{would}\:{have} \\ $$$${to}\:{decompose}\:{the}\:{inequality}\:{to}\:{a} \\ $$$${form}\:{that}\:{the}\:{information}\:{we}\:{have} \\ $$$${about}\:{the}\:{situation}\:{is}\:{satisfies}.\:{The} \\ $$$${AM}−{GM}\:{sadly}\:{didn}'{t}\:{help}\:{as}\:{I}\:{had} \\ $$$${hoped}\:{it}\:{would}\:{because}\:{while}\:{it} \\ $$$${shows}\:{that}\: \\ $$$$\frac{\left({x}+{y}+{z}\right)^{\mathrm{2}} }{\mathrm{4}}\geqslant\sqrt{\underset{{r}=\mathrm{1}} {\overset{\mathrm{4}} {\prod}}{a}_{{r}} } \\ $$$${it}\:{cannot}\:{solely}\:{lead}\:{one}\:{to}\:{safely}\:{stating} \\ $$$${that}\:\frac{\left({x}+{y}+{z}\right)^{\mathrm{2}} }{\mathrm{3}\sqrt{\mathrm{3}}}\geqslant\sqrt{\underset{{r}=\mathrm{1}} {\overset{\mathrm{4}} {\prod}}{a}_{{r}} }\:. \\ $$$$ \\ $$$${The}\:{transitive}\:{property}\:{of}\:{inequalities} \\ $$$${wouldn}'{t}\:{have}\:{worked}\:{for}\:{us}\:{in}\:{this} \\ $$$${approach}\::\left(\:.\right. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Yozzii last updated on 14/Dec/15

$${Say}\:{we}\:{have}\:{the}\:{following}\:\:{problem}. \\ $$$$−−−−−−−−−−−−−−−−−−−−− \\ $$$${We}\:{want}\:{to}\:{show}\:{p}>{q}.\:{We}\:{have}\:{that} \\ $$$${r}>{q}\:{and}\:{r}={np}\:{where}\:{n},{p},{q}\in\mathbb{R}^{+} \\ $$$$\therefore\:\:{np}>{q}\Rightarrow{p}>\frac{\mathrm{1}}{{n}}{q}.\:\:{q}=\sqrt{\underset{{r}=\mathrm{1}} {\overset{\mathrm{4}} {\prod}}{a}_{{r}} }. \\ $$$$ \\ $$$${Let}\:{p}=\frac{{u}}{\mathrm{3}\sqrt{\mathrm{3}}}\:{and}\:{r}=\frac{{u}}{\mathrm{4}}\:,{u}=\left({x}+{y}+{z}\right)^{\mathrm{2}} . \\ $$$${u}=\mathrm{3}{p}\sqrt{\mathrm{3}}\Rightarrow{r}=\frac{\mathrm{3}{p}\sqrt{\mathrm{3}}}{\mathrm{4}}\Rightarrow\:{n}=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{4}}. \\ $$$$\therefore\:{p}>\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}{q}\: \\ $$$$\frac{\mathrm{16}}{\mathrm{27}}=\left(\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} \Rightarrow\:\mathrm{0}<\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}<\mathrm{1}. \\ $$$$\therefore\:{The}\:{information}\:{only}\:{shows}\:{that} \\ $$$${p}>\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}{q}\:{and}\:{not}\:{p}>{q}\:{since}\:\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}{q}<{q}. \\ $$$${On}\:{a}\:{number}\:{line}\:{we}\:{have}\:{three}\:{cases} \\ $$$${due}\:{to}\:{this}\:{result}: \\ $$$$\left({i}\right)\:\:\:\overset{\rightarrow} {\mathrm{0}}...............\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}{q}........{p}....{q}.... \\ $$$$\left({ii}\right)\:\overset{\rightarrow} {\mathrm{0}}...............\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}{q}........{q}....{p}..... \\ $$$$\left({iii}\right)\overset{\rightarrow} {\mathrm{0}}..............\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}{q}.......{p}={q}...... \\ $$$${Which}\:{is}\:{correct}? \\ $$
Commented by Rasheed Soomro last updated on 15/Dec/15

$$\mathcal{T}^{\mathcal{H}^{\mathcal{A}} \mathcal{N}} \mathcal{K}_{\mathcal{S}{sss}} ! \\ $$
Commented by Yozzii last updated on 14/Dec/15

$${Let}\:{r}>\mathrm{7}\:{and}\:{r}=\mathrm{1}.\mathrm{2}{p}. \\ $$$$\therefore\mathrm{1}.\mathrm{2}{p}>\mathrm{7}\Rightarrow{p}>\frac{\mathrm{7}}{\mathrm{1}.\mathrm{2}}\:{but}\:{this} \\ $$$${doesn}'{t}\:{show}\:{that}\:{p}>\mathrm{7}. \\ $$$$ \\ $$$$\:{Similarly}, \\ $$$$\frac{\left({z}+{y}+{x}\right)^{\mathrm{2}} }{\mathrm{4}}\geqslant\sqrt{\underset{{r}=\mathrm{1}} {\overset{\mathrm{4}} {\prod}}{a}_{{r}} } \\ $$$$\Rightarrow\left({x}+{y}+{z}\right)^{\mathrm{2}} \geqslant\mathrm{4}\sqrt{\underset{{r}=\mathrm{1}} {\overset{\mathrm{4}} {\prod}}{a}_{{r}} } \\ $$$$\Rightarrow\frac{\left({x}+{y}+{z}\right)^{\mathrm{2}} }{\mathrm{3}\sqrt{\mathrm{3}}}\geqslant\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}\sqrt{\underset{{r}=\mathrm{1}} {\overset{\mathrm{4}} {\prod}}{a}_{{r}} }\ngeq\sqrt{\underset{{r}=\mathrm{1}} {\overset{\mathrm{4}} {\prod}}{a}_{{r}} }\:{since}\:\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}\ngtr\mathrm{1} \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 15/Dec/15
$$\boldsymbol{\mathcal{T}}\mathcal{H}\alpha{n}\boldsymbol{\mathcal{N}}\Bbbk\mathcal{S}^{\mathcal{SS}{Sssss}!} \\ $$
Answered by Yozzi last updated on 12/Dec/15

$${For}\:{a}\:{triangle}\:{with}\:{side}\:{lengths} \\ $$$${x},{y}\:{and}\:{z},\:{the}\:{length}\:{of}\:{one}\:{side} \\ $$$${cannot}\:{exceed}\:{the}\:{sum}\:{of}\:{the}\:{lengths} \\ $$$${of}\:{the}\:{other}\:{two}\:{sides}.\:{Symbolically}, \\ $$$${x}+{y}−{z}\geqslant\mathrm{0}\:\wedge\:{x}+{z}−{y}\geqslant\mathrm{0}\:\wedge\:{z}+{y}−{x}\geqslant\mathrm{0}. \\ $$$$ \\ $$$$\mathrm{PROOF}:\:{Suppose}\:{for}\:{contradiction} \\ $$$${that}\:{one}\:{side}\:{of}\:{length}\:\boldsymbol{{a}}\:{of}\:{a}\:{given} \\ $$$${triangle}\:{is}\:{more}\:{than}\:{the}\:{sum}\:{of}\:{the} \\ $$$${lengths}\:{of}\:{the}\:{other}\:{two}\:{sides},\:{denoted} \\ $$$${by}\:\boldsymbol{{b}}\:{and}\:\boldsymbol{{c}}.\: \\ $$$$\therefore\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{a}}>\boldsymbol{{b}}+\boldsymbol{{c}} \\ $$$${with}\:\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}}>\mathrm{0}. \\ $$$$\Rightarrow\:\boldsymbol{{a}}^{\mathrm{2}} >\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{c}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{{bc}} \\ $$$$\Rightarrow\:\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{{c}}^{\mathrm{2}} >\mathrm{2}\boldsymbol{{bc}}\:\:\:\:\:\:\left(\ast\right) \\ $$$${By}\:{the}\:{cosine}\:{rule},\: \\ $$$$\boldsymbol{{a}}^{\mathrm{2}} =\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{c}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{bc}}{cos}\theta \\ $$$${where}\:\theta\:{is}\:{the}\:{angle}\:{subtended}\:{by}\:{the} \\ $$$${meeting}\:{of}\:{the}\:{sides}\:\boldsymbol{{b}}\:{and}\:\boldsymbol{{c}},\:{opposite} \\ $$$${to}\:\boldsymbol{{a}}. \\ $$$$\Rightarrow\:\:−\mathrm{2}\boldsymbol{{bc}}{cos}\theta=\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{{c}}^{\mathrm{2}} \\ $$$$\therefore\:\:−\mathrm{2}\boldsymbol{{bc}}{cos}\theta>\mathrm{2}\boldsymbol{{bc}}\Rightarrow{cos}\theta<−\mathrm{1} \\ $$$$\Rightarrow\:\mid{cos}\theta\mid>\mathrm{1}.\:{But},\:\forall\theta\in\mathbb{R},\:\mid{cos}\theta\mid\leqslant\mathrm{1}. \\ $$$${This}\:{is}\:{a}\:{contradiction},\:{so}\:{that}\: \\ $$$${indeed}\:\boldsymbol{{a}}\leqslant\boldsymbol{{b}}+\boldsymbol{{c}}\:{in}\:{general}\:{and}\:{we} \\ $$$${can}\:{show}\:{that}\:\boldsymbol{{b}}\leqslant\boldsymbol{{a}}+\boldsymbol{{c}}\:{and}\:\boldsymbol{{c}}\leqslant\boldsymbol{{a}}+\boldsymbol{{b}} \\ $$$${likewise},\:{for}\:\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}}>\mathrm{0}.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Box \\ $$$${Hence},\:{all}\:{terms}\:{under}\:{the}\:{square} \\ $$$${root}\:{of}\:{Mr}.\:{Rasheed}'{s}\:{rhs}\:{expression} \\ $$$${are}\:{non}−{negative}.\: \\ $$$$ \\ $$$$ \\ $$$${Since}\:{all}\:{terms}\:{are}\:{positive}\:{reals},\:{by}\:{AM}−{GM}, \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left(\left\{{x}+{y}+{z}\right\}+\left\{{x}+{y}−{z}\right\}+\left\{{x}+{z}−{y}\right\}+\left\{{z}+{y}−{x}\right\}\right)\geqslant\left(\left({x}+{y}+{z}\right)\left({x}+{y}−{z}\right)\left({z}+{y}−{x}\right)\left({x}+{z}−{y}\right)\right)^{\mathrm{1}/\mathrm{4}} \\ $$$${a}_{\mathrm{1}} ={x}+{y}+{z},\:\:{a}_{\mathrm{2}} ={x}+{y}−{z} \\ $$$${a}_{\mathrm{3}} ={x}+{z}−{y},\:\:{a}_{\mathrm{4}} ={z}+{y}−{x} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}\left({x}+{y}+{z}\right)\right)\geqslant\left(\underset{{r}=\mathrm{1}} {\overset{\mathrm{4}} {\prod}}{a}_{{r}} \right)^{\mathrm{1}/\mathrm{4}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}\left({x}+{y}+{z}\right)^{\mathrm{2}} \geqslant\sqrt{\underset{{r}=\mathrm{1}} {\overset{\mathrm{4}} {\prod}}{a}_{{r}} } \\ $$$$ \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 12/Dec/15
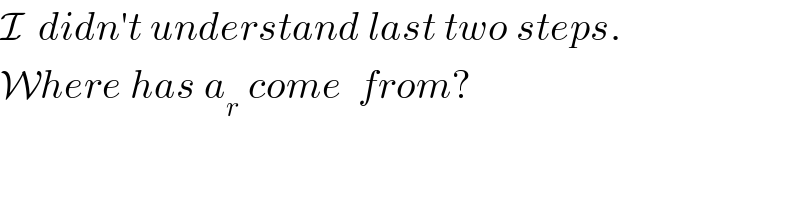
$$\mathcal{I}\:\:{didn}'{t}\:{understand}\:{last}\:{two}\:{steps}. \\ $$$$\mathcal{W}{here}\:{has}\:{a}_{{r}} \:{come}\:\:{from}? \\ $$
Commented by Yozzi last updated on 12/Dec/15
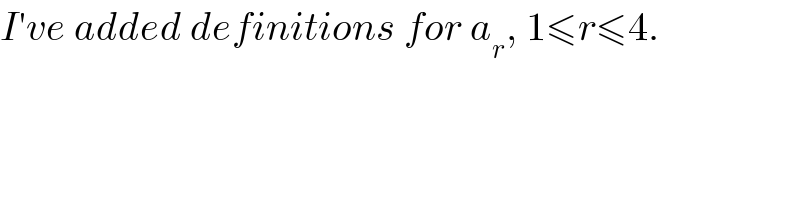
$${I}'{ve}\:{added}\:{definitions}\:{for}\:{a}_{{r}} ,\:\mathrm{1}\leqslant{r}\leqslant\mathrm{4}. \\ $$
