
Previous in Relation and Functions Next in Relation and Functions
Question Number 33094 by abdo imad last updated on 10/Apr/18
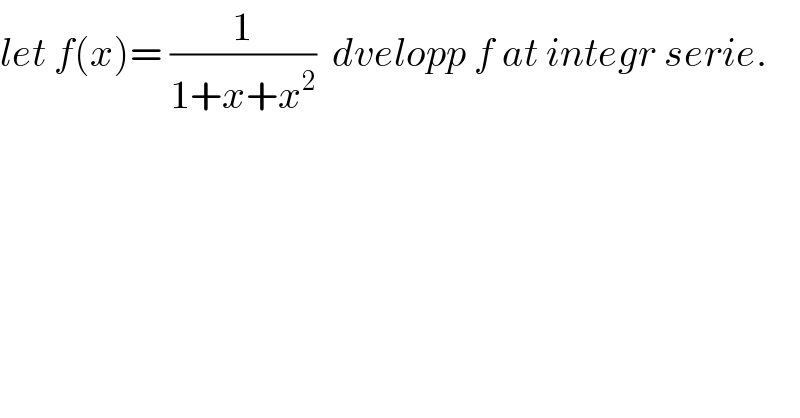
$${let}\:{f}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{1}+{x}+{x}^{\mathrm{2}} }\:\:{dvelopp}\:{f}\:{at}\:{integr}\:{serie}. \\ $$
Commented by prof Abdo imad last updated on 11/Apr/18
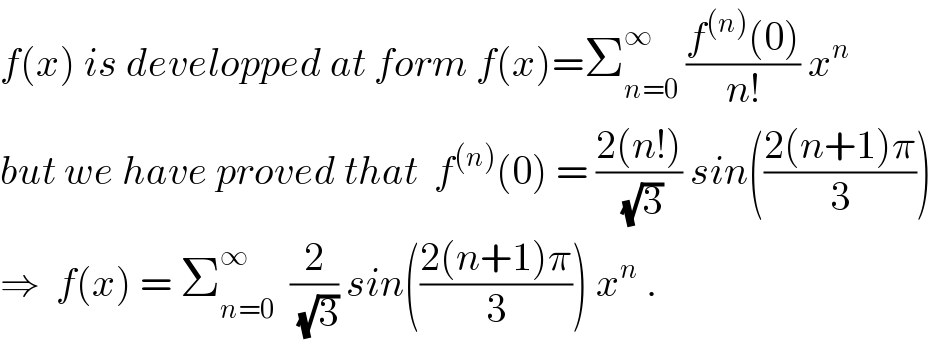
$${f}\left({x}\right)\:{is}\:{developped}\:{at}\:{form}\:{f}\left({x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}\:{x}^{{n}} \\ $$$${but}\:{we}\:{have}\:{proved}\:{that}\:\:{f}^{\left({n}\right)} \left(\mathrm{0}\right)\:=\:\frac{\mathrm{2}\left({n}!\right)}{\sqrt{\mathrm{3}}}\:{sin}\left(\frac{\mathrm{2}\left({n}+\mathrm{1}\right)\pi}{\mathrm{3}}\right) \\ $$$$\Rightarrow\:\:{f}\left({x}\right)\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:{sin}\left(\frac{\mathrm{2}\left({n}+\mathrm{1}\right)\pi}{\mathrm{3}}\right)\:{x}^{{n}} \:. \\ $$
