Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 53736 by Mikael_Marshall last updated on 25/Jan/19

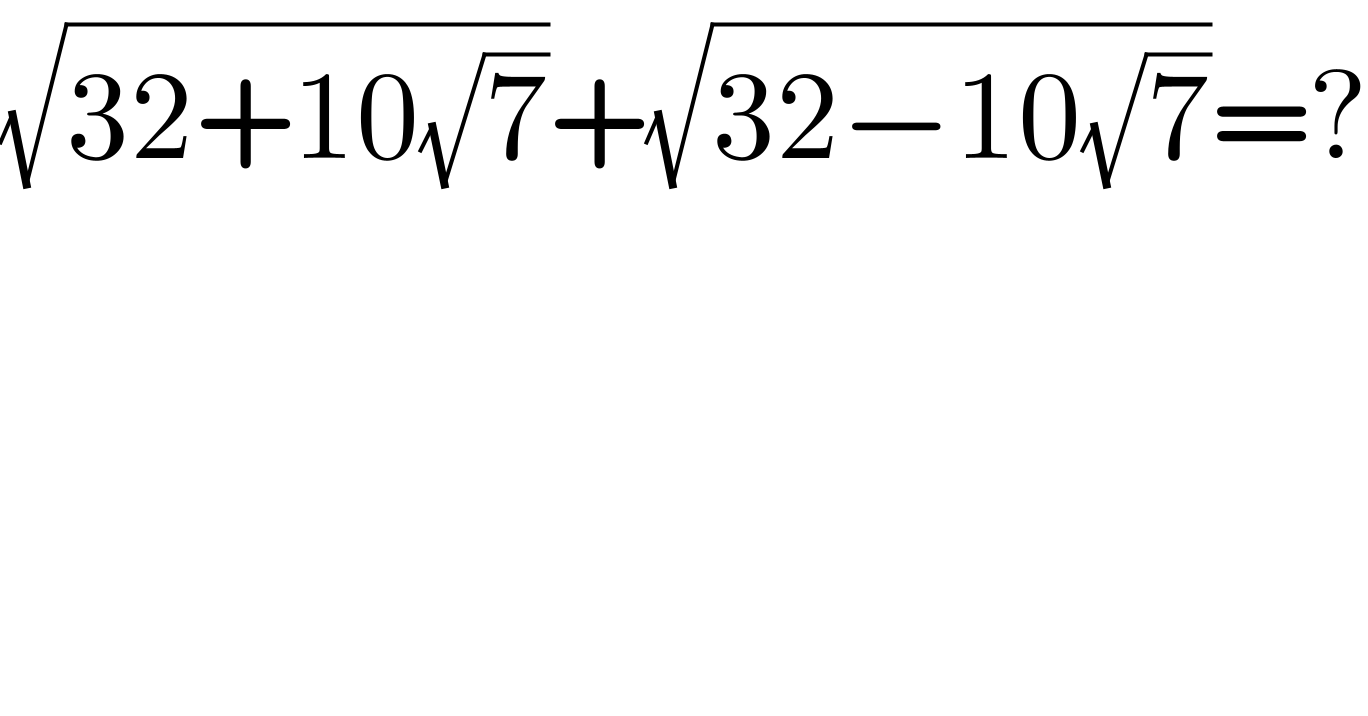
(√(32+10(√7)))+(√(32−10(√7)))=?

$$\sqrt{\mathrm{32}+\mathrm{10}\sqrt{\mathrm{7}}}+\sqrt{\mathrm{32}−\mathrm{10}\sqrt{\mathrm{7}}}=? \\ $$

Commented by Kunal12588 last updated on 25/Jan/19

just want to add something (√(m+(√(n )))) getting square root of a surd (√(m+(√n)))=(√a)+(√b) m+(√n)=a+b+2(√(ab)) a+b=m (1) 4ab=n a^2 +b^2 +2ab−4ab=m^2 −n (a−b)^2 =m^2 −n a−b=(√(m^2 −n)) (2) from (1) and (2) a=((m+(√(m^2 −n)))/2), b=((m−(√(m^2 −n)))/2) ∴(√(m+(√n)))=(√((m+(√(m^2 −n)))/2))+(√((m−(√(m^2 −n)))/2)) given question (√(32+10(√7)))=(√((32+(√(1024−700)))/2))+(√((32−(√(1024−700)))/2)) =(√((32+18)/2))+(√((32−18)/2))=(√(25))+(√7)=5+(√7) similarly (√(32−10(√7)))=5−(√7)

$${just}\:{want}\:{to}\:{add}\:{something} \\ $$$$\sqrt{{m}+\sqrt{{n}\:}}\:{getting}\:{square}\:{root}\:{of}\:{a}\:{surd} \\ $$$$\sqrt{{m}+\sqrt{{n}}}=\sqrt{{a}}+\sqrt{{b}} \\ $$$${m}+\sqrt{{n}}={a}+{b}+\mathrm{2}\sqrt{{ab}} \\ $$$${a}+{b}={m}\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{4}{ab}={n} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}−\mathrm{4}{ab}={m}^{\mathrm{2}} −{n} \\ $$$$\left({a}−{b}\right)^{\mathrm{2}} ={m}^{\mathrm{2}} −{n} \\ $$$${a}−{b}=\sqrt{{m}^{\mathrm{2}} −{n}}\:\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$${from}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right) \\ $$$${a}=\frac{{m}+\sqrt{{m}^{\mathrm{2}} −{n}}}{\mathrm{2}},\:\:{b}=\frac{{m}−\sqrt{{m}^{\mathrm{2}} −{n}}}{\mathrm{2}} \\ $$$$\therefore\sqrt{{m}+\sqrt{{n}}}=\sqrt{\frac{{m}+\sqrt{{m}^{\mathrm{2}} −{n}}}{\mathrm{2}}}+\sqrt{\frac{{m}−\sqrt{{m}^{\mathrm{2}} −{n}}}{\mathrm{2}}} \\ $$$${given}\:{question} \\ $$$$\sqrt{\mathrm{32}+\mathrm{10}\sqrt{\mathrm{7}}}=\sqrt{\frac{\mathrm{32}+\sqrt{\mathrm{1024}−\mathrm{700}}}{\mathrm{2}}}+\sqrt{\frac{\mathrm{32}−\sqrt{\mathrm{1024}−\mathrm{700}}}{\mathrm{2}}} \\ $$$$=\sqrt{\frac{\mathrm{32}+\mathrm{18}}{\mathrm{2}}}+\sqrt{\frac{\mathrm{32}−\mathrm{18}}{\mathrm{2}}}=\sqrt{\mathrm{25}}+\sqrt{\mathrm{7}}=\mathrm{5}+\sqrt{\mathrm{7}} \\ $$$${similarly}\:\sqrt{\mathrm{32}−\mathrm{10}\sqrt{\mathrm{7}}}=\mathrm{5}−\sqrt{\mathrm{7}} \\ $$

Commented by maxmathsup by imad last updated on 25/Jan/19

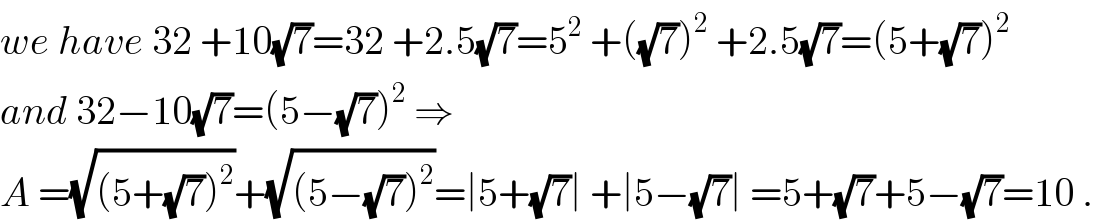
we have 32 +10(√7)=32 +2.5(√7)=5^2 +((√7))^2 +2.5(√7)=(5+(√7))^2 and 32−10(√7)=(5−(√7))^2 ⇒ A =(√((5+(√7))^2 ))+(√((5−(√7))^2 ))=∣5+(√7)∣ +∣5−(√7)∣ =5+(√7)+5−(√7)=10 .

$${we}\:{have}\:\mathrm{32}\:+\mathrm{10}\sqrt{\mathrm{7}}=\mathrm{32}\:+\mathrm{2}.\mathrm{5}\sqrt{\mathrm{7}}=\mathrm{5}^{\mathrm{2}} \:+\left(\sqrt{\mathrm{7}}\right)^{\mathrm{2}} \:+\mathrm{2}.\mathrm{5}\sqrt{\mathrm{7}}=\left(\mathrm{5}+\sqrt{\mathrm{7}}\right)^{\mathrm{2}} \\ $$$${and}\:\mathrm{32}−\mathrm{10}\sqrt{\mathrm{7}}=\left(\mathrm{5}−\sqrt{\mathrm{7}}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$${A}\:=\sqrt{\left(\mathrm{5}+\sqrt{\mathrm{7}}\right)^{\mathrm{2}} }+\sqrt{\left(\mathrm{5}−\sqrt{\mathrm{7}}\right)^{\mathrm{2}} }=\mid\mathrm{5}+\sqrt{\mathrm{7}}\mid\:+\mid\mathrm{5}−\sqrt{\mathrm{7}}\mid\:=\mathrm{5}+\sqrt{\mathrm{7}}+\mathrm{5}−\sqrt{\mathrm{7}}=\mathrm{10}\:. \\ $$

Commented by maxmathsup by imad last updated on 26/Jan/19

you are welcome.

$${you}\:{are}\:{welcome}. \\ $$

Commented by Mikael_Marshall last updated on 26/Jan/19

thank you

$${thank}\:{you} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 25/Jan/19

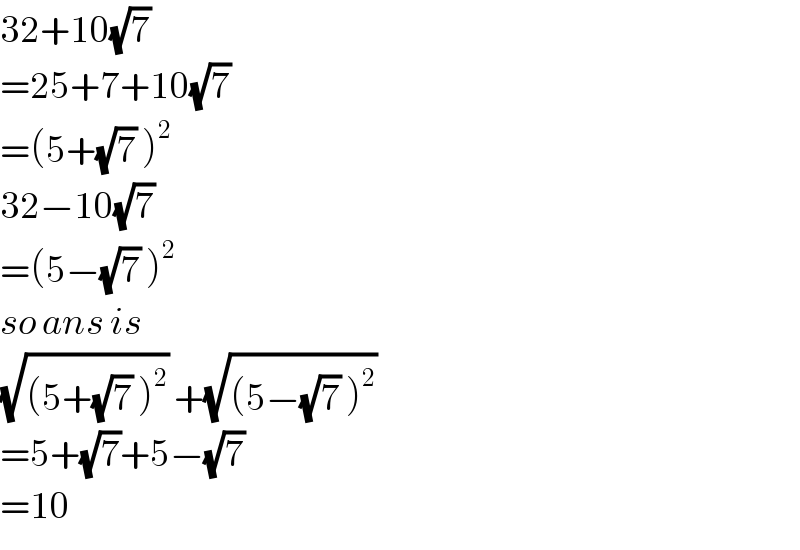
32+10(√7) =25+7+10(√7) =(5+(√7) )^2 32−10(√7) =(5−(√7) )^2 so ans is (√((5+(√7) )^2 )) +(√((5−(√7) )^2 )) =5+(√7)+5−(√7) =10

$$\mathrm{32}+\mathrm{10}\sqrt{\mathrm{7}}\: \\ $$$$=\mathrm{25}+\mathrm{7}+\mathrm{10}\sqrt{\mathrm{7}}\: \\ $$$$=\left(\mathrm{5}+\sqrt{\mathrm{7}}\:\right)^{\mathrm{2}} \\ $$$$\mathrm{32}−\mathrm{10}\sqrt{\mathrm{7}}\: \\ $$$$=\left(\mathrm{5}−\sqrt{\mathrm{7}}\:\right)^{\mathrm{2}} \\ $$$${so}\:{ans}\:{is} \\ $$$$\sqrt{\left(\mathrm{5}+\sqrt{\mathrm{7}}\:\right)^{\mathrm{2}} }\:+\sqrt{\left(\mathrm{5}−\sqrt{\mathrm{7}}\:\right)^{\mathrm{2}} }\: \\ $$$$=\mathrm{5}+\sqrt{\mathrm{7}}+\mathrm{5}−\sqrt{\mathrm{7}}\: \\ $$$$=\mathrm{10} \\ $$

Commented by Mikael_Marshall last updated on 26/Jan/19

thanks so much

$${thanks}\:{so}\:{much} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 26/Jan/19

most welcome...

$${most}\:{welcome}... \\ $$

Answered by ajfour last updated on 25/Jan/19

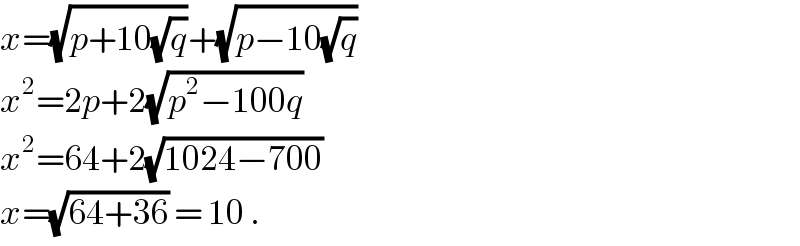
x=(√(p+10(√q)))+(√(p−10(√q))) x^2 =2p+2(√(p^2 −100q)) x^2 =64+2(√(1024−700)) x=(√(64+36)) = 10 .

$${x}=\sqrt{{p}+\mathrm{10}\sqrt{{q}}}+\sqrt{{p}−\mathrm{10}\sqrt{{q}}} \\ $$$${x}^{\mathrm{2}} =\mathrm{2}{p}+\mathrm{2}\sqrt{{p}^{\mathrm{2}} −\mathrm{100}{q}} \\ $$$${x}^{\mathrm{2}} =\mathrm{64}+\mathrm{2}\sqrt{\mathrm{1024}−\mathrm{700}} \\ $$$${x}=\sqrt{\mathrm{64}+\mathrm{36}}\:=\:\mathrm{10}\:. \\ $$

Commented by Mikael_Marshall last updated on 26/Jan/19

thank you so much.

$${thank}\:{you}\:{so}\:{much}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com