
Question Number 31030 by abdo imad last updated on 02/Mar/18
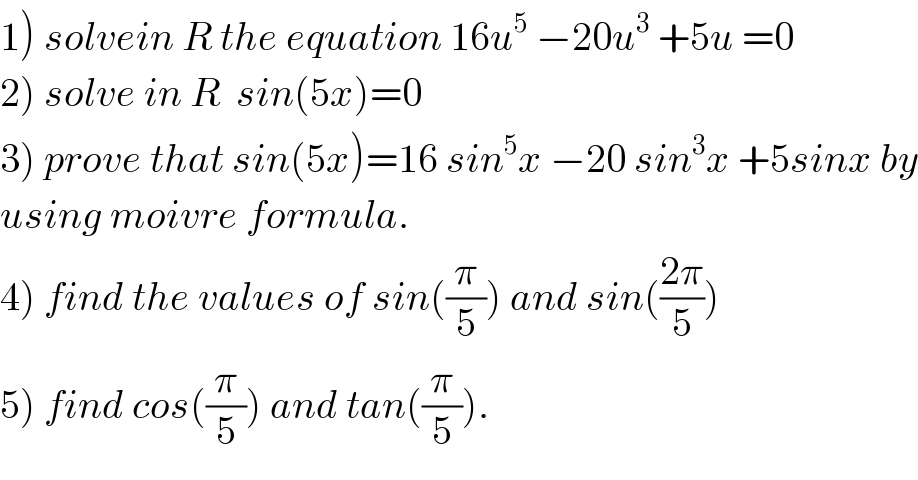
$$\left.\mathrm{1}\right)\:{solvein}\:{R}\:{the}\:{equation}\:\mathrm{16}{u}^{\mathrm{5}} \:−\mathrm{20}{u}^{\mathrm{3}} \:+\mathrm{5}{u}\:=\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\:{solve}\:{in}\:{R}\:\:{sin}\left(\mathrm{5}{x}\right)=\mathrm{0} \\ $$$$\left.\mathrm{3}\right)\:{prove}\:{that}\:{sin}\left(\mathrm{5}{x}\right)=\mathrm{16}\:{sin}^{\mathrm{5}} {x}\:−\mathrm{20}\:{sin}^{\mathrm{3}} {x}\:+\mathrm{5}{sinx}\:{by} \\ $$$${using}\:{moivre}\:{formula}. \\ $$$$\left.\mathrm{4}\right)\:{find}\:{the}\:{values}\:{of}\:{sin}\left(\frac{\pi}{\mathrm{5}}\right)\:{and}\:{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{5}}\right) \\ $$$$\left.\mathrm{5}\right)\:{find}\:{cos}\left(\frac{\pi}{\mathrm{5}}\right)\:{and}\:{tan}\left(\frac{\pi}{\mathrm{5}}\right). \\ $$
