
Question Number 307 by userid1 last updated on 25/Jan/15
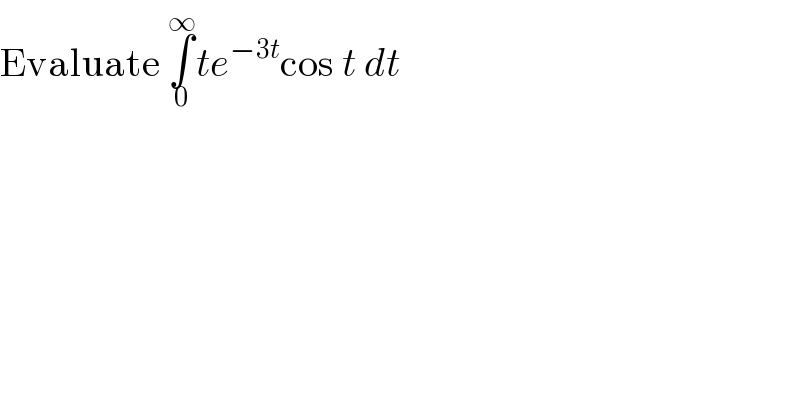
$$\mathrm{Evaluate}\:\underset{\mathrm{0}} {\overset{\infty} {\int}}{te}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}\:{dt} \\ $$
Commented by 123456 last updated on 20/Dec/14
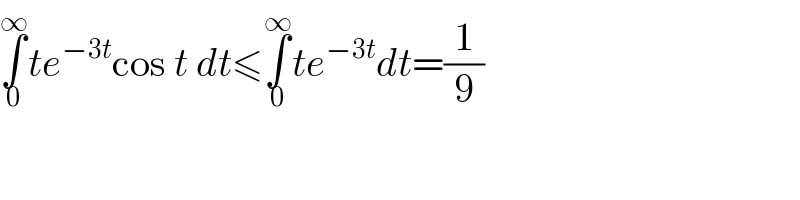
$$\underset{\mathrm{0}} {\overset{\infty} {\int}}{te}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}\:{dt}\leqslant\underset{\mathrm{0}} {\overset{\infty} {\int}}{te}^{−\mathrm{3}{t}} {dt}=\frac{\mathrm{1}}{\mathrm{9}} \\ $$
Answered by 123456 last updated on 20/Dec/14
![part 1/? ∫_0 ^∞ te^(−3t) cos t dt=lim_(ε→∞) ∫_0 ^ε te^(−3t) cos t dt ∫te^(−3t) cos t dt u=tcos t⇒du=cos t−tsin tdt dv=e^(−3t) dt⇒v=−(1/3)e^(−3t) =−(1/3)te^(−3t) cos t+(1/3)∫e^(−3t) (cos t−tsin t)dt =−(1/3)te^(−3t) cos t+(1/3)∫e^(−3t) cos t dt−(1/3)∫e^(−3t) tsin tdt u=tsin t⇒du=sin t+tcos tdt dv=e^(−3t) dt⇒v=−(1/3)e^(−3t) =−(1/3)te^(−3t) cos t+(1/3)∫e^(−3t) cos t dt−(1/3)[−(1/3)te^(−3t) sin t+(1/3)∫e^(−3t) (sin t+tcos t)dt] =−(1/3)te^(−3t) cos t+(1/3)∫e^(−3t) cos t dt+(1/9)te^(−3t) sin t−(1/9)∫e^(−3t) sin t dt−(1/9)∫e^(−3t) tcos t dt lets I=∫e^(−3t) tcos t dt I=−(1/3)te^(−3t) cos t+(1/3)∫e^(−3t) cos t dt+(1/9)te^(−3t) sin t−(1/9)∫e^(−3t) sin t dt−(1/9)I ((10)/9)I=−(1/3)te^(−3t) cos t+(1/3)∫e^(−3t) cos t dt+(1/9)te^(−3t) sin t−(1/9)∫e^(−3t) sin t dt ∫e^(−3t) tcos t dt=(9/(10))(−(1/3)te^(−3t) cos t+(1/3)∫e^(−3t) cos t dt+(1/9)te^(−3t) sin t−(1/9)∫e^(−3t) sin t dt) from where solve blue and red and then put the limits](Q312.png)
$$\mathrm{part}\:\mathrm{1}/? \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}{te}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}\:{dt}=\underset{\epsilon\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{0}} {\overset{\epsilon} {\int}}{te}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}\:{dt} \\ $$$$\int{te}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}\:{dt} \\ $$$${u}={t}\mathrm{cos}\:{t}\Rightarrow{du}=\mathrm{cos}\:{t}−{t}\mathrm{sin}\:{tdt} \\ $$$${dv}={e}^{−\mathrm{3}{t}} {dt}\Rightarrow{v}=−\frac{\mathrm{1}}{\mathrm{3}}{e}^{−\mathrm{3}{t}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{te}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}+\frac{\mathrm{1}}{\mathrm{3}}\int{e}^{−\mathrm{3}{t}} \left(\mathrm{cos}\:{t}−{t}\mathrm{sin}\:{t}\right){dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{te}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}+\frac{\mathrm{1}}{\mathrm{3}}\int{e}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}\:{dt}−\frac{\mathrm{1}}{\mathrm{3}}\int{e}^{−\mathrm{3}{t}} {t}\mathrm{sin}\:{tdt} \\ $$$${u}=\mathrm{tsin}\:\mathrm{t}\Rightarrow{du}=\mathrm{sin}\:{t}+{t}\mathrm{cos}\:{tdt} \\ $$$${dv}={e}^{−\mathrm{3}{t}} {dt}\Rightarrow{v}=−\frac{\mathrm{1}}{\mathrm{3}}{e}^{−\mathrm{3}{t}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{te}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}+\frac{\mathrm{1}}{\mathrm{3}}\int{e}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}\:{dt}−\frac{\mathrm{1}}{\mathrm{3}}\left[−\frac{\mathrm{1}}{\mathrm{3}}{te}^{−\mathrm{3}{t}} \mathrm{sin}\:{t}+\frac{\mathrm{1}}{\mathrm{3}}\int{e}^{−\mathrm{3}{t}} \left(\mathrm{sin}\:{t}+{t}\mathrm{cos}\:{t}\right){dt}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{te}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}+\frac{\mathrm{1}}{\mathrm{3}}\int{e}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}\:{dt}+\frac{\mathrm{1}}{\mathrm{9}}{te}^{−\mathrm{3}{t}} \mathrm{sin}\:{t}−\frac{\mathrm{1}}{\mathrm{9}}\int{e}^{−\mathrm{3}{t}} \mathrm{sin}\:{t}\:{dt}−\frac{\mathrm{1}}{\mathrm{9}}\int{e}^{−\mathrm{3}{t}} {t}\mathrm{cos}\:{t}\:{dt} \\ $$$$\mathrm{lets}\:\mathrm{I}=\int{e}^{−\mathrm{3}{t}} {t}\mathrm{cos}\:{t}\:{dt} \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{3}}{te}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}+\frac{\mathrm{1}}{\mathrm{3}}\int{e}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}\:{dt}+\frac{\mathrm{1}}{\mathrm{9}}{te}^{−\mathrm{3}{t}} \mathrm{sin}\:{t}−\frac{\mathrm{1}}{\mathrm{9}}\int{e}^{−\mathrm{3}{t}} \mathrm{sin}\:{t}\:{dt}−\frac{\mathrm{1}}{\mathrm{9}}\mathrm{I} \\ $$$$\frac{\mathrm{10}}{\mathrm{9}}\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{3}}{te}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}+\frac{\mathrm{1}}{\mathrm{3}}\int{e}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}\:{dt}+\frac{\mathrm{1}}{\mathrm{9}}{te}^{−\mathrm{3}{t}} \mathrm{sin}\:{t}−\frac{\mathrm{1}}{\mathrm{9}}\int{e}^{−\mathrm{3}{t}} \mathrm{sin}\:{t}\:{dt} \\ $$$$\int{e}^{−\mathrm{3}{t}} {t}\mathrm{cos}\:{t}\:{dt}=\frac{\mathrm{9}}{\mathrm{10}}\left(−\frac{\mathrm{1}}{\mathrm{3}}{te}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}+\frac{\mathrm{1}}{\mathrm{3}}\int{e}^{−\mathrm{3}{t}} \mathrm{cos}\:{t}\:{dt}+\frac{\mathrm{1}}{\mathrm{9}}{te}^{−\mathrm{3}{t}} \mathrm{sin}\:{t}−\frac{\mathrm{1}}{\mathrm{9}}\int{e}^{−\mathrm{3}{t}} \mathrm{sin}\:{t}\:{dt}\right) \\ $$$$\mathrm{from}\:\mathrm{where}\:\mathrm{solve}\:\mathrm{blue}\:\mathrm{and}\:\mathrm{red}\:\mathrm{and}\:\mathrm{then}\:\mathrm{put}\:\mathrm{the}\:\mathrm{limits} \\ $$
