
Question Number 30087 by rahul 19 last updated on 16/Feb/18
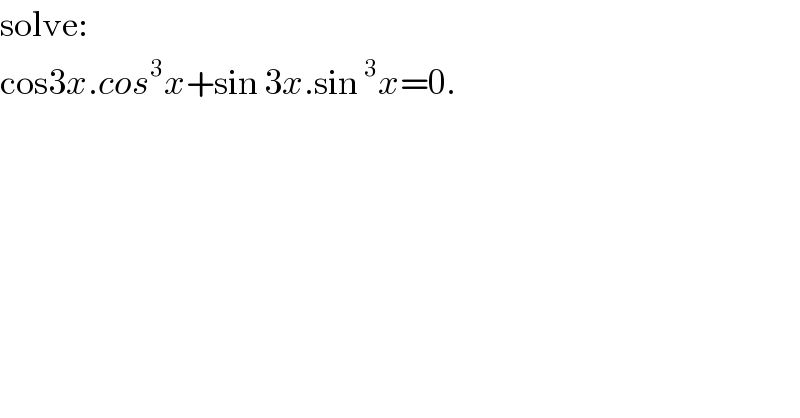
$$\mathrm{solve}: \\ $$$$\mathrm{cos3}{x}.{cos}^{\mathrm{3}} {x}+\mathrm{sin}\:\mathrm{3}{x}.\mathrm{sin}\:^{\mathrm{3}} {x}=\mathrm{0}. \\ $$
Answered by MJS last updated on 16/Feb/18
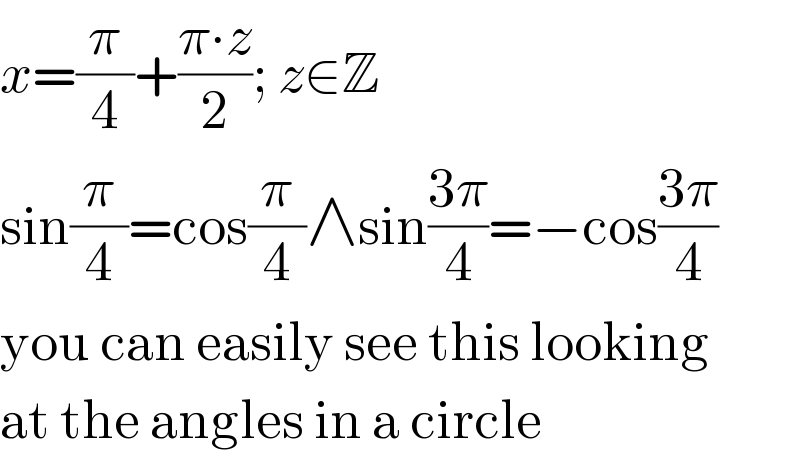
$${x}=\frac{\pi}{\mathrm{4}}+\frac{\pi\centerdot{z}}{\mathrm{2}};\:{z}\in\mathbb{Z} \\ $$$$\mathrm{sin}\frac{\pi}{\mathrm{4}}=\mathrm{cos}\frac{\pi}{\mathrm{4}}\wedge\mathrm{sin}\frac{\mathrm{3}\pi}{\mathrm{4}}=−\mathrm{cos}\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$$\mathrm{you}\:\mathrm{can}\:\mathrm{easily}\:\mathrm{see}\:\mathrm{this}\:\mathrm{looking} \\ $$$$\mathrm{at}\:\mathrm{the}\:\mathrm{angles}\:\mathrm{in}\:\mathrm{a}\:\mathrm{circle} \\ $$
Answered by MJS last updated on 16/Feb/18
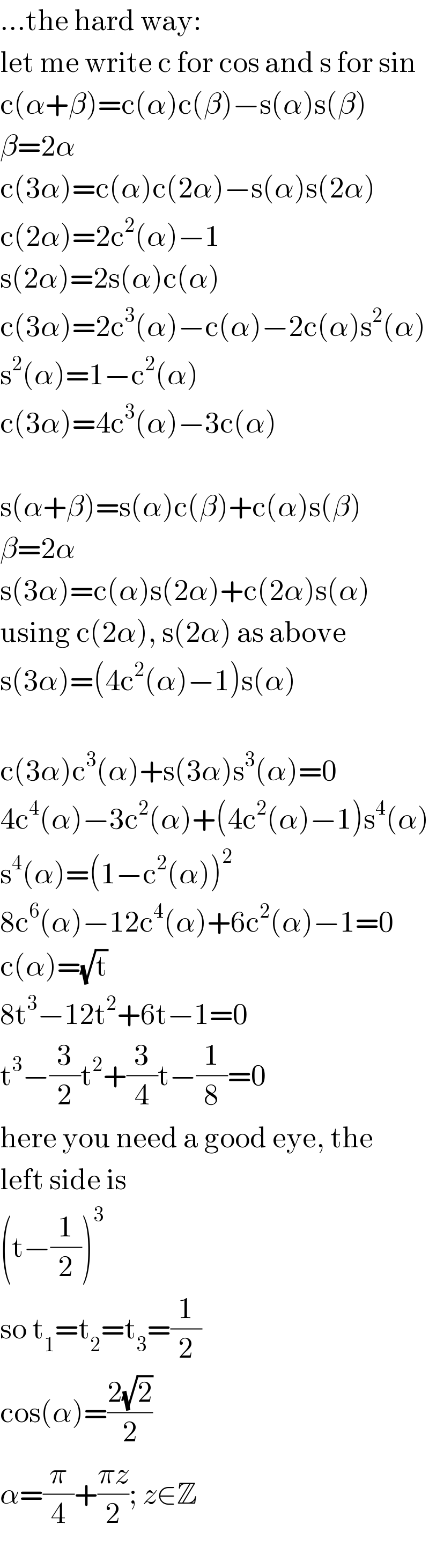
$$...\mathrm{the}\:\mathrm{hard}\:\mathrm{way}: \\ $$$$\mathrm{let}\:\mathrm{me}\:\mathrm{write}\:\mathrm{c}\:\mathrm{for}\:\mathrm{cos}\:\mathrm{and}\:\mathrm{s}\:\mathrm{for}\:\mathrm{sin} \\ $$$$\mathrm{c}\left(\alpha+\beta\right)=\mathrm{c}\left(\alpha\right)\mathrm{c}\left(\beta\right)−\mathrm{s}\left(\alpha\right)\mathrm{s}\left(\beta\right) \\ $$$$\beta=\mathrm{2}\alpha \\ $$$$\mathrm{c}\left(\mathrm{3}\alpha\right)=\mathrm{c}\left(\alpha\right)\mathrm{c}\left(\mathrm{2}\alpha\right)−\mathrm{s}\left(\alpha\right)\mathrm{s}\left(\mathrm{2}\alpha\right) \\ $$$$\mathrm{c}\left(\mathrm{2}\alpha\right)=\mathrm{2c}^{\mathrm{2}} \left(\alpha\right)−\mathrm{1} \\ $$$$\mathrm{s}\left(\mathrm{2}\alpha\right)=\mathrm{2s}\left(\alpha\right)\mathrm{c}\left(\alpha\right) \\ $$$$\mathrm{c}\left(\mathrm{3}\alpha\right)=\mathrm{2c}^{\mathrm{3}} \left(\alpha\right)−\mathrm{c}\left(\alpha\right)−\mathrm{2c}\left(\alpha\right)\mathrm{s}^{\mathrm{2}} \left(\alpha\right) \\ $$$$\mathrm{s}^{\mathrm{2}} \left(\alpha\right)=\mathrm{1}−\mathrm{c}^{\mathrm{2}} \left(\alpha\right) \\ $$$$\mathrm{c}\left(\mathrm{3}\alpha\right)=\mathrm{4c}^{\mathrm{3}} \left(\alpha\right)−\mathrm{3c}\left(\alpha\right) \\ $$$$ \\ $$$$\mathrm{s}\left(\alpha+\beta\right)=\mathrm{s}\left(\alpha\right)\mathrm{c}\left(\beta\right)+\mathrm{c}\left(\alpha\right)\mathrm{s}\left(\beta\right) \\ $$$$\beta=\mathrm{2}\alpha \\ $$$$\mathrm{s}\left(\mathrm{3}\alpha\right)=\mathrm{c}\left(\alpha\right)\mathrm{s}\left(\mathrm{2}\alpha\right)+\mathrm{c}\left(\mathrm{2}\alpha\right)\mathrm{s}\left(\alpha\right) \\ $$$$\mathrm{using}\:\mathrm{c}\left(\mathrm{2}\alpha\right),\:\mathrm{s}\left(\mathrm{2}\alpha\right)\:\mathrm{as}\:\mathrm{above} \\ $$$$\mathrm{s}\left(\mathrm{3}\alpha\right)=\left(\mathrm{4c}^{\mathrm{2}} \left(\alpha\right)−\mathrm{1}\right)\mathrm{s}\left(\alpha\right) \\ $$$$ \\ $$$$\mathrm{c}\left(\mathrm{3}\alpha\right)\mathrm{c}^{\mathrm{3}} \left(\alpha\right)+\mathrm{s}\left(\mathrm{3}\alpha\right)\mathrm{s}^{\mathrm{3}} \left(\alpha\right)=\mathrm{0} \\ $$$$\mathrm{4c}^{\mathrm{4}} \left(\alpha\right)−\mathrm{3c}^{\mathrm{2}} \left(\alpha\right)+\left(\mathrm{4c}^{\mathrm{2}} \left(\alpha\right)−\mathrm{1}\right)\mathrm{s}^{\mathrm{4}} \left(\alpha\right) \\ $$$$\mathrm{s}^{\mathrm{4}} \left(\alpha\right)=\left(\mathrm{1}−\mathrm{c}^{\mathrm{2}} \left(\alpha\right)\right)^{\mathrm{2}} \\ $$$$\mathrm{8c}^{\mathrm{6}} \left(\alpha\right)−\mathrm{12c}^{\mathrm{4}} \left(\alpha\right)+\mathrm{6c}^{\mathrm{2}} \left(\alpha\right)−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{c}\left(\alpha\right)=\sqrt{\mathrm{t}} \\ $$$$\mathrm{8t}^{\mathrm{3}} −\mathrm{12t}^{\mathrm{2}} +\mathrm{6t}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{t}^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{2}}\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\mathrm{t}−\frac{\mathrm{1}}{\mathrm{8}}=\mathrm{0} \\ $$$$\mathrm{here}\:\mathrm{you}\:\mathrm{need}\:\mathrm{a}\:\mathrm{good}\:\mathrm{eye},\:\mathrm{the} \\ $$$$\mathrm{left}\:\mathrm{side}\:\mathrm{is} \\ $$$$\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} \\ $$$$\mathrm{so}\:\mathrm{t}_{\mathrm{1}} =\mathrm{t}_{\mathrm{2}} =\mathrm{t}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{cos}\left(\alpha\right)=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\alpha=\frac{\pi}{\mathrm{4}}+\frac{\pi{z}}{\mathrm{2}};\:{z}\in\mathbb{Z} \\ $$
Commented by rahul 19 last updated on 16/Feb/18

$$\mathrm{thanks}. \\ $$
Answered by ajfour last updated on 16/Feb/18
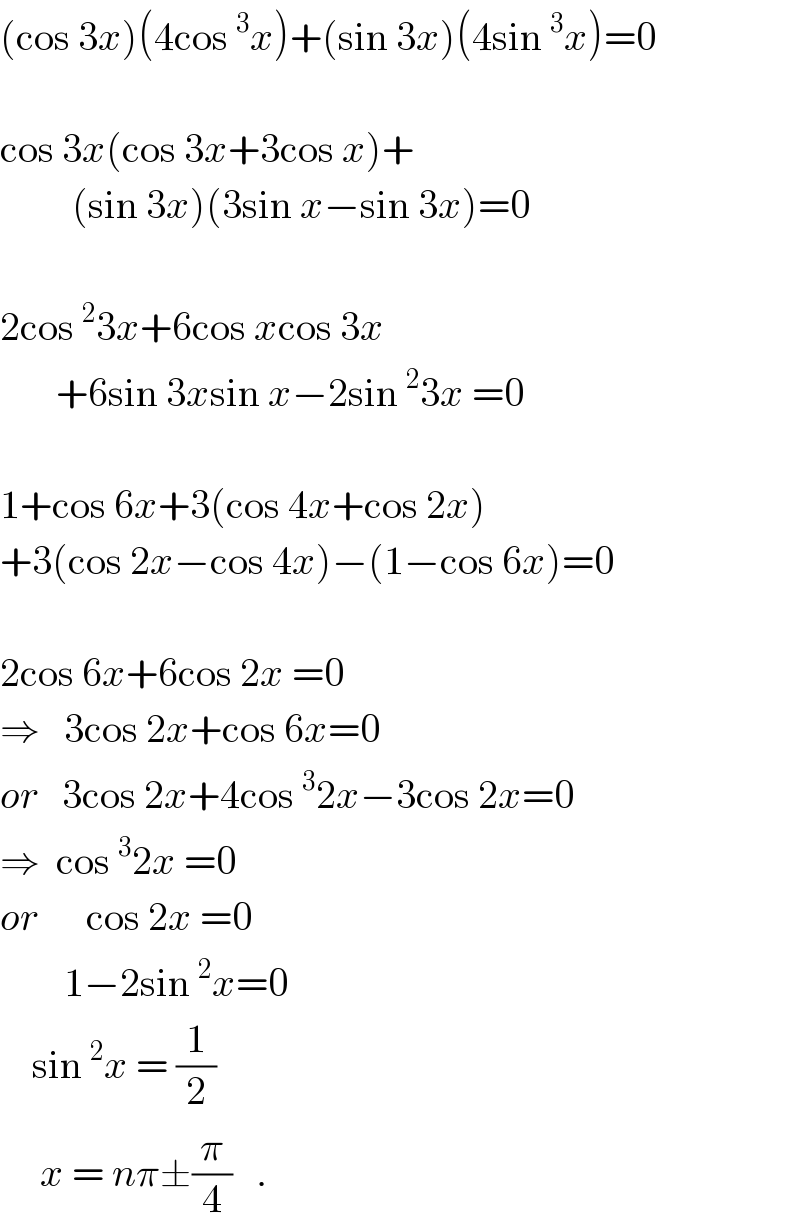
$$\left(\mathrm{cos}\:\mathrm{3}{x}\right)\left(\mathrm{4cos}\:^{\mathrm{3}} {x}\right)+\left(\mathrm{sin}\:\mathrm{3}{x}\right)\left(\mathrm{4sin}\:^{\mathrm{3}} {x}\right)=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{cos}\:\mathrm{3}{x}\left(\mathrm{cos}\:\mathrm{3}{x}+\mathrm{3cos}\:{x}\right)+ \\ $$$$\:\:\:\:\:\:\:\:\:\left(\mathrm{sin}\:\mathrm{3}{x}\right)\left(\mathrm{3sin}\:{x}−\mathrm{sin}\:\mathrm{3}{x}\right)=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{2cos}\:^{\mathrm{2}} \mathrm{3}{x}+\mathrm{6cos}\:{x}\mathrm{cos}\:\mathrm{3}{x} \\ $$$$\:\:\:\:\:\:\:+\mathrm{6sin}\:\mathrm{3}{x}\mathrm{sin}\:{x}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{3}{x}\:=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{1}+\mathrm{cos}\:\mathrm{6}{x}+\mathrm{3}\left(\mathrm{cos}\:\mathrm{4}{x}+\mathrm{cos}\:\mathrm{2}{x}\right) \\ $$$$+\mathrm{3}\left(\mathrm{cos}\:\mathrm{2}{x}−\mathrm{cos}\:\mathrm{4}{x}\right)−\left(\mathrm{1}−\mathrm{cos}\:\mathrm{6}{x}\right)=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{2cos}\:\mathrm{6}{x}+\mathrm{6cos}\:\mathrm{2}{x}\:=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{3cos}\:\mathrm{2}{x}+\mathrm{cos}\:\mathrm{6}{x}=\mathrm{0} \\ $$$${or}\:\:\:\mathrm{3cos}\:\mathrm{2}{x}+\mathrm{4cos}\:^{\mathrm{3}} \mathrm{2}{x}−\mathrm{3cos}\:\mathrm{2}{x}=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{cos}\:^{\mathrm{3}} \mathrm{2}{x}\:=\mathrm{0} \\ $$$${or}\:\:\:\:\:\:\mathrm{cos}\:\mathrm{2}{x}\:=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}=\mathrm{0} \\ $$$$\:\:\:\:\mathrm{sin}\:^{\mathrm{2}} {x}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:{x}\:=\:{n}\pi\pm\frac{\pi}{\mathrm{4}}\:\:\:. \\ $$
Commented by rahul 19 last updated on 16/Feb/18

$$\mathrm{thank}\:\mathrm{u}\:\mathrm{sir}. \\ $$
