
Question Number 191795 by 073 last updated on 30/Apr/23

$$\mathrm{3}^{\mathrm{x}} −\mathrm{2}^{\mathrm{x}} =\mathrm{19} \\ $$$$\mathrm{x}=?? \\ $$
Commented by mr W last updated on 30/Apr/23

$${we}\:{know}\:\mathrm{27}−\mathrm{8}=\mathrm{19}, \\ $$$${i}.{e}.\:\mathrm{3}^{\mathrm{3}} −\mathrm{2}^{\mathrm{3}} =\mathrm{19} \\ $$$${therefore}\:{x}=\mathrm{3}. \\ $$$${there}\:{is}\:{no}\:{other}\:{smart}\:{method}\:{you} \\ $$$${can}\:{blindly}\:{apply}\:{to}\:{calculate}\:{the} \\ $$$${root}.\:{for}\:{example}\:{you}\:{can}'{t}\:{solve} \\ $$$$\mathrm{3}^{{x}} −\mathrm{2}^{{x}} =\mathrm{20}\:{exactly}. \\ $$
Answered by deleteduser1 last updated on 30/Apr/23
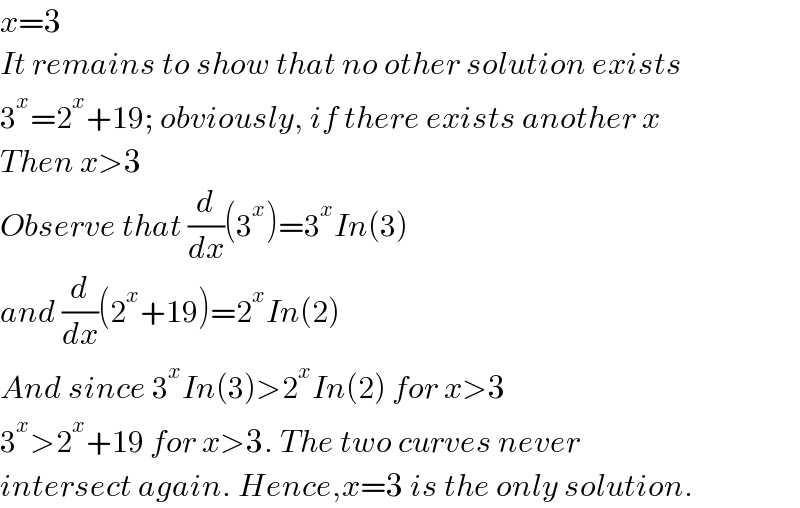
$${x}=\mathrm{3} \\ $$$${It}\:{remains}\:{to}\:{show}\:{that}\:{no}\:{other}\:{solution}\:{exists} \\ $$$$\mathrm{3}^{{x}} =\mathrm{2}^{{x}} +\mathrm{19};\:{obviously},\:{if}\:{there}\:{exists}\:{another}\:{x} \\ $$$${Then}\:{x}>\mathrm{3} \\ $$$${Observe}\:{that}\:\frac{{d}}{{dx}}\left(\mathrm{3}^{{x}} \right)=\mathrm{3}^{{x}} {In}\left(\mathrm{3}\right) \\ $$$${and}\:\frac{{d}}{{dx}}\left(\mathrm{2}^{{x}} +\mathrm{19}\right)=\mathrm{2}^{{x}} {In}\left(\mathrm{2}\right) \\ $$$${And}\:{since}\:\mathrm{3}^{{x}} {In}\left(\mathrm{3}\right)>\mathrm{2}^{{x}} {In}\left(\mathrm{2}\right)\:{for}\:{x}>\mathrm{3} \\ $$$$\mathrm{3}^{{x}} >\mathrm{2}^{{x}} +\mathrm{19}\:{for}\:{x}>\mathrm{3}.\:{The}\:{two}\:{curves}\:{never}\: \\ $$$${intersect}\:{again}.\:{Hence},{x}=\mathrm{3}\:{is}\:{the}\:{only}\:{solution}. \\ $$
