Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 129958 by bemath last updated on 21/Jan/21

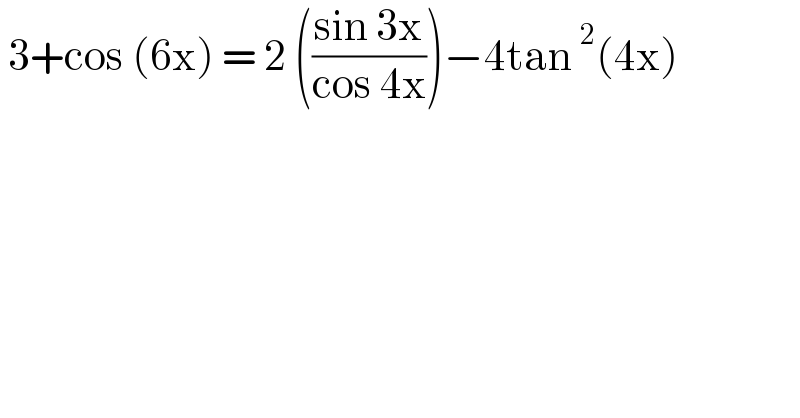
3+cos (6x) = 2 (((sin 3x)/(cos 4x)))−4tan^2 (4x)

$$\:\mathrm{3}+\mathrm{cos}\:\left(\mathrm{6x}\right)\:=\:\mathrm{2}\:\left(\frac{\mathrm{sin}\:\mathrm{3x}}{\mathrm{cos}\:\mathrm{4x}}\right)−\mathrm{4tan}\:^{\mathrm{2}} \left(\mathrm{4x}\right) \\ $$

Answered by MJS_new last updated on 21/Jan/21

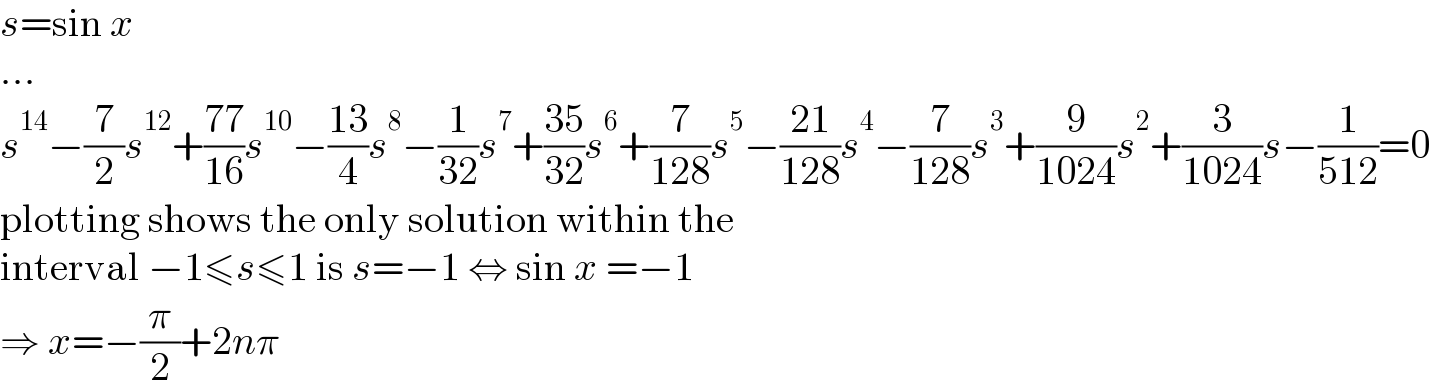
s=sin x ... s^(14) −(7/2)s^(12) +((77)/(16))s^(10) −((13)/4)s^8 −(1/(32))s^7 +((35)/(32))s^6 +(7/(128))s^5 −((21)/(128))s^4 −(7/(128))s^3 +(9/(1024))s^2 +(3/(1024))s−(1/(512))=0 plotting shows the only solution within the interval −1≤s≤1 is s=−1 ⇔ sin x =−1 ⇒ x=−(π/2)+2nπ

$${s}=\mathrm{sin}\:{x} \\ $$$$... \\ $$$${s}^{\mathrm{14}} −\frac{\mathrm{7}}{\mathrm{2}}{s}^{\mathrm{12}} +\frac{\mathrm{77}}{\mathrm{16}}{s}^{\mathrm{10}} −\frac{\mathrm{13}}{\mathrm{4}}{s}^{\mathrm{8}} −\frac{\mathrm{1}}{\mathrm{32}}{s}^{\mathrm{7}} +\frac{\mathrm{35}}{\mathrm{32}}{s}^{\mathrm{6}} +\frac{\mathrm{7}}{\mathrm{128}}{s}^{\mathrm{5}} −\frac{\mathrm{21}}{\mathrm{128}}{s}^{\mathrm{4}} −\frac{\mathrm{7}}{\mathrm{128}}{s}^{\mathrm{3}} +\frac{\mathrm{9}}{\mathrm{1024}}{s}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{1024}}{s}−\frac{\mathrm{1}}{\mathrm{512}}=\mathrm{0} \\ $$$$\mathrm{plotting}\:\mathrm{shows}\:\mathrm{the}\:\mathrm{only}\:\mathrm{solution}\:\mathrm{within}\:\mathrm{the} \\ $$$$\mathrm{interval}\:−\mathrm{1}\leqslant{s}\leqslant\mathrm{1}\:\mathrm{is}\:{s}=−\mathrm{1}\:\Leftrightarrow\:\mathrm{sin}\:{x}\:=−\mathrm{1} \\ $$$$\Rightarrow\:{x}=−\frac{\pi}{\mathrm{2}}+\mathrm{2}{n}\pi \\ $$

Commented by EDWIN88 last updated on 22/Jan/21

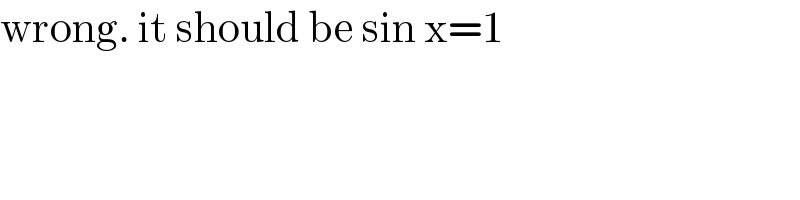
wrong. it should be sin x=1

$$\mathrm{wrong}.\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{sin}\:\mathrm{x}=\mathrm{1} \\ $$

Commented by MJS_new last updated on 22/Jan/21

no. you forgot to test your solution with x=(π/2) in the given equation you get 2=−2 within 0≤x<2π the only solution is ((3π)/2)

$$\mathrm{no}.\:\mathrm{you}\:\mathrm{forgot}\:\mathrm{to}\:\mathrm{test}\:\mathrm{your}\:\mathrm{solution} \\ $$$$\mathrm{with}\:{x}=\frac{\pi}{\mathrm{2}}\:\mathrm{in}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{you}\:\mathrm{get}\:\mathrm{2}=−\mathrm{2} \\ $$$$\mathrm{within}\:\mathrm{0}\leqslant{x}<\mathrm{2}\pi\:\mathrm{the}\:\mathrm{only}\:\mathrm{solution}\:\mathrm{is}\:\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$

Answered by EDWIN88 last updated on 22/Jan/21

3 +cos 6x = ((2sin 3x)/(cos 4x)) −((4sin^2 4x)/(cos^2 4x)) 3cos^2 4x+cos^2 4x cos 6x=2sin 3xcos 4x−4sin^2 4x 3cos^2 4x+cos^2 4x cos 6x=2sin 3x cos 4x−4+4cos^2 4x cos^2 4x cos 6x = 2sin 3x cos 4x−4+cos^2 4x cos^2 4x (1−2sin^2 3x)=2sin 3x cos 4x+cos^2 4x−4 cos^2 4x−2sin^2 3x cos^2 4x = 2sin 3x cos 4x +cos^2 4x−4 2sin^2 3x cos^2 4x +2sin 3x cos 3x −4=0 (sin 3x cos 4x)^2 +sin 3x cos 4x−2=0 let sin 3x cos 4x = y y^2 +y−2=0 →(y−1)(y+2)=0 for y = 1 ⇒sin 3x cos 4x=1 for y=−2⇒sin 3x cos 4x = −2 { ((sin 3x=3sin x−4sin^3 x)),((cos 4x=1−2sin^2 2x =1−2(4sin^2 x cos^2 x))) :} cos 4x = 1−8sin^2 x(1−sin^2 x) = 1−8sin^2 x+8sin^4 x (∗)(3sin x−4sin^3 x)(8sin^4 x−8sin^2 x+1)−1=0 24sin^5 x−24sin^3 x+3sin x−32sin^7 x+32sin^5 x−4sin^3 x−1=0 −32sin^7 x+56sin^5 x−28sin^3 x+3sin x−1=0 (sin x+1)(−32sin^6 x+32sin^5 x+24sin^4 x−24sin^3 x−4sin^2 x+4sin x−1)=0 ⇔ sin x = −1=sin (−(π/2)) x = 2nπ−(π/2) ; n∈Z

$$\mathrm{3}\:+\mathrm{cos}\:\mathrm{6x}\:=\:\frac{\mathrm{2sin}\:\mathrm{3x}}{\mathrm{cos}\:\mathrm{4x}}\:−\frac{\mathrm{4sin}\:^{\mathrm{2}} \mathrm{4x}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{4x}} \\ $$$$\mathrm{3cos}\:^{\mathrm{2}} \mathrm{4x}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{4x}\:\mathrm{cos}\:\mathrm{6x}=\mathrm{2sin}\:\mathrm{3xcos}\:\mathrm{4x}−\mathrm{4sin}\:^{\mathrm{2}} \mathrm{4x} \\ $$$$\mathrm{3cos}\:^{\mathrm{2}} \mathrm{4x}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{4x}\:\mathrm{cos}\:\mathrm{6x}=\mathrm{2sin}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{4x}−\mathrm{4}+\mathrm{4cos}\:^{\mathrm{2}} \mathrm{4x} \\ $$$$\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{4x}\:\mathrm{cos}\:\mathrm{6x}\:=\:\mathrm{2sin}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{4x}−\mathrm{4}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{4x} \\ $$$$\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{4x}\:\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{3x}\right)=\mathrm{2sin}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{4x}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{4x}−\mathrm{4} \\ $$$$\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{4x}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{3x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{4x}\:=\:\mathrm{2sin}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{4x}\:+\mathrm{cos}\:^{\mathrm{2}} \mathrm{4x}−\mathrm{4} \\ $$$$\:\mathrm{2sin}\:^{\mathrm{2}} \mathrm{3x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{4x}\:+\mathrm{2sin}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{3x}\:−\mathrm{4}=\mathrm{0} \\ $$$$\:\left(\mathrm{sin}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{4x}\right)^{\mathrm{2}} +\mathrm{sin}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{4x}−\mathrm{2}=\mathrm{0} \\ $$$$\:\mathrm{let}\:\mathrm{sin}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{4x}\:=\:\mathrm{y} \\ $$$$\:\mathrm{y}^{\mathrm{2}} +\mathrm{y}−\mathrm{2}=\mathrm{0}\:\rightarrow\left(\mathrm{y}−\mathrm{1}\right)\left(\mathrm{y}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\:\mathrm{for}\:\mathrm{y}\:=\:\mathrm{1}\:\Rightarrow\mathrm{sin}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{4x}=\mathrm{1} \\ $$$$\:\mathrm{for}\:\mathrm{y}=−\mathrm{2}\Rightarrow\mathrm{sin}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{4x}\:=\:−\mathrm{2} \\ $$$$\begin{cases}{\mathrm{sin}\:\mathrm{3x}=\mathrm{3sin}\:\mathrm{x}−\mathrm{4sin}\:^{\mathrm{3}} \mathrm{x}}\\{\mathrm{cos}\:\mathrm{4x}=\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{2x}\:=\mathrm{1}−\mathrm{2}\left(\mathrm{4sin}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\right)}\end{cases} \\ $$$$\:\:\mathrm{cos}\:\mathrm{4x}\:=\:\mathrm{1}−\mathrm{8sin}\:^{\mathrm{2}} \mathrm{x}\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}−\mathrm{8sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{8sin}\:^{\mathrm{4}} \mathrm{x}\: \\ $$$$\:\left(\ast\right)\left(\mathrm{3sin}\:\mathrm{x}−\mathrm{4sin}\:^{\mathrm{3}} \mathrm{x}\right)\left(\mathrm{8sin}\:^{\mathrm{4}} \mathrm{x}−\mathrm{8sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{1}\right)−\mathrm{1}=\mathrm{0} \\ $$$$\:\mathrm{24sin}\:^{\mathrm{5}} \mathrm{x}−\mathrm{24sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{3sin}\:\mathrm{x}−\mathrm{32sin}\:^{\mathrm{7}} \mathrm{x}+\mathrm{32sin}\:^{\mathrm{5}} \mathrm{x}−\mathrm{4sin}\:^{\mathrm{3}} \mathrm{x}−\mathrm{1}=\mathrm{0} \\ $$$$−\mathrm{32sin}\:^{\mathrm{7}} \mathrm{x}+\mathrm{56sin}\:^{\mathrm{5}} \mathrm{x}−\mathrm{28sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{3sin}\:\mathrm{x}−\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{sin}\:\mathrm{x}+\mathrm{1}\right)\left(−\mathrm{32sin}\:^{\mathrm{6}} \mathrm{x}+\mathrm{32sin}\:^{\mathrm{5}} \mathrm{x}+\mathrm{24sin}\:^{\mathrm{4}} \mathrm{x}−\mathrm{24sin}\:^{\mathrm{3}} \mathrm{x}−\mathrm{4sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{4sin}\:\mathrm{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\:\mathrm{sin}\:\mathrm{x}\:=\:−\mathrm{1}=\mathrm{sin}\:\left(−\frac{\pi}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\mathrm{x}\:=\:\mathrm{2n}\pi−\frac{\pi}{\mathrm{2}}\:;\:\mathrm{n}\in\mathbb{Z} \\ $$

Commented by MJS_new last updated on 22/Jan/21

thank you for checking it again

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{checking}\:\mathrm{it}\:\mathrm{again} \\ $$

Commented by EDWIN88 last updated on 22/Jan/21

thanks too

$$\mathrm{thanks}\:\mathrm{too} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com