
Question Number 95919 by Abdulrahman last updated on 28/May/20
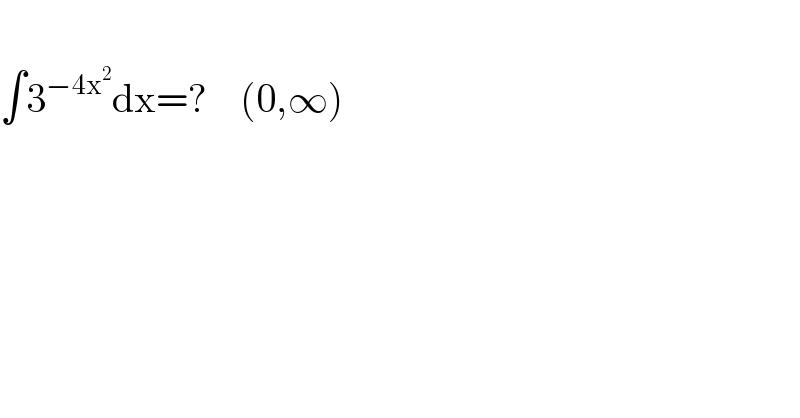
$$ \\ $$$$\int\mathrm{3}^{−\mathrm{4x}^{\mathrm{2}} } \mathrm{dx}=?\:\:\:\:\left(\mathrm{0},\infty\right) \\ $$
Answered by mathmax by abdo last updated on 28/May/20
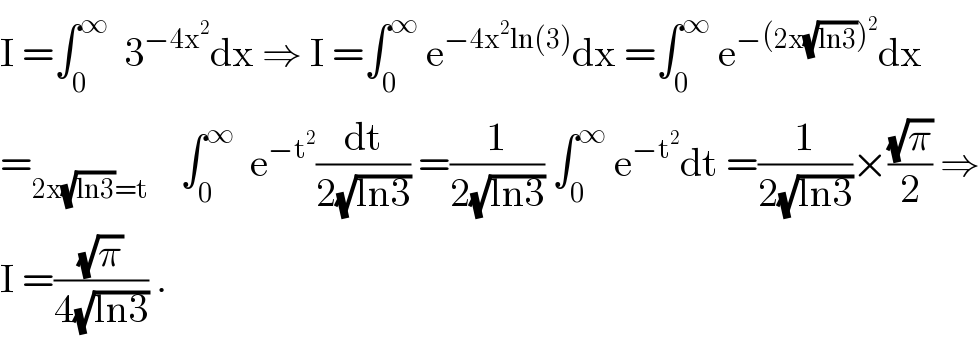
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{3}^{−\mathrm{4x}^{\mathrm{2}} } \mathrm{dx}\:\Rightarrow\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{4x}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{3}\right)} \mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{2x}\sqrt{\mathrm{ln3}}\right)^{\mathrm{2}} } \mathrm{dx} \\ $$$$=_{\mathrm{2x}\sqrt{\mathrm{ln3}}=\mathrm{t}} \:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \frac{\mathrm{dt}}{\mathrm{2}\sqrt{\mathrm{ln3}}}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{ln3}}}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{ln3}}}×\frac{\sqrt{\pi}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\sqrt{\pi}}{\mathrm{4}\sqrt{\mathrm{ln3}}}\:. \\ $$
Commented by Abdulrahman last updated on 28/May/20

$$\mathrm{why}\:\mathrm{ln}\left(\mathrm{3}\right)???? \\ $$
Commented by bobhans last updated on 28/May/20
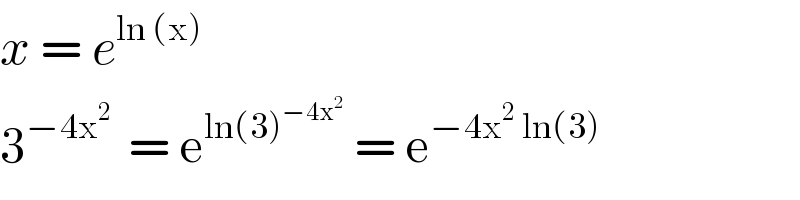
$${x}\:=\:{e}^{\mathrm{ln}\:\left(\mathrm{x}\right)\:} \\ $$$$\mathrm{3}^{−\mathrm{4x}^{\mathrm{2}} \:} \:=\:\mathrm{e}^{\mathrm{ln}\left(\mathrm{3}\right)^{−\mathrm{4x}^{\mathrm{2}} } } \:=\:\mathrm{e}^{−\mathrm{4x}^{\mathrm{2}} \:\mathrm{ln}\left(\mathrm{3}\right)\:} \\ $$
Commented by Abdulrahman last updated on 28/May/20
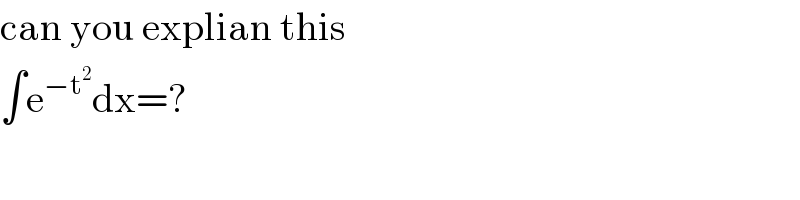
$$\mathrm{can}\:\mathrm{you}\:\mathrm{explian}\:\mathrm{this} \\ $$$$\int\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dx}=? \\ $$
Commented by prakash jain last updated on 28/May/20
https://en.m.wikipedia.org/wiki/Gaussian_integral This explain gaussian integral
