
Question Number 126666 by bramlexs22 last updated on 23/Dec/20

$$\:\mathrm{3}+\mathrm{33}+\mathrm{333}+\mathrm{3333}+...+\underset{\mathrm{2020}\:{times}} {\underbrace{\mathrm{3333}...\mathrm{3}}}\: \\ $$$${divide}\:{by}\:\mathrm{2}.\:{find}\:{the}\:{remainder} \\ $$
Answered by JDamian last updated on 23/Dec/20

$${it}\:{is}\:{easy} \\ $$$$\mathrm{0} \\ $$
Answered by liberty last updated on 23/Dec/20
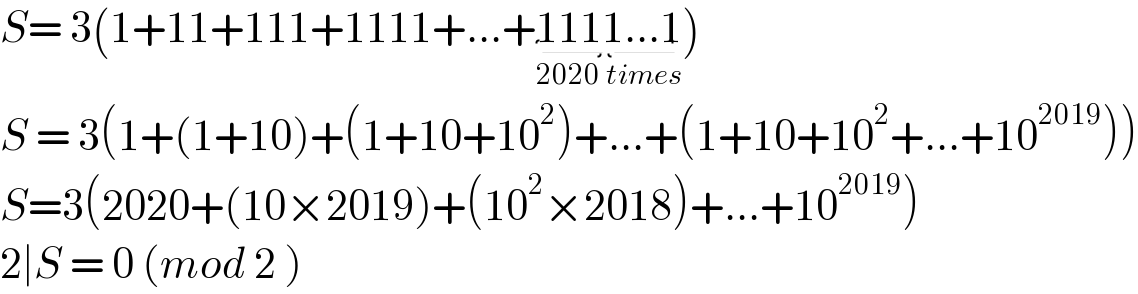
$${S}=\:\mathrm{3}\left(\mathrm{1}+\mathrm{11}+\mathrm{111}+\mathrm{1111}+...+\underset{\mathrm{2020}\:{times}} {\underbrace{\mathrm{1111}...\mathrm{1}}}\right) \\ $$$${S}\:=\:\mathrm{3}\left(\mathrm{1}+\left(\mathrm{1}+\mathrm{10}\right)+\left(\mathrm{1}+\mathrm{10}+\mathrm{10}^{\mathrm{2}} \right)+...+\left(\mathrm{1}+\mathrm{10}+\mathrm{10}^{\mathrm{2}} +...+\mathrm{10}^{\mathrm{2019}} \right)\right) \\ $$$${S}=\mathrm{3}\left(\mathrm{2020}+\left(\mathrm{10}×\mathrm{2019}\right)+\left(\mathrm{10}^{\mathrm{2}} ×\mathrm{2018}\right)+...+\mathrm{10}^{\mathrm{2019}} \right) \\ $$$$\mathrm{2}\mid{S}\:=\:\mathrm{0}\:\left({mod}\:\mathrm{2}\:\right) \\ $$
Answered by talminator2856791 last updated on 23/Dec/20

$$\: \\ $$$$\:\mathrm{to}\:\mathrm{find}\:\mathrm{remainder}\:\mathrm{of}\:\mathrm{3}+\mathrm{33}+\mathrm{333}+.......+\underset{\mathrm{2020}\:\mathrm{times}} {\underbrace{\mathrm{3333}......\mathrm{3}}}\: \\ $$$$\:\mathrm{is}\:\mathrm{equivalent}\:\mathrm{finding}\:\mathrm{whether}\:\mathrm{it}\:\mathrm{is}\:\mathrm{even}\:\mathrm{or}\:\mathrm{odd}. \\ $$$$\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{any}\:\mathrm{two}\:\mathrm{odd}\:\mathrm{numbers}\:\mathrm{is}\:\mathrm{even}. \\ $$$$\:\mathrm{any}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{10}\:\mathrm{is}\:\mathrm{even}\:\left(\mathrm{as}\:\mathrm{10}\:\mathrm{is}\:\mathrm{even}\right) \\ $$$$\: \\ $$$$\:{k}\:=\:\mathrm{3}+\mathrm{33}+\mathrm{333}+......+\underset{\mathrm{2020}\:\mathrm{times}} {\underbrace{\mathrm{3333}....\mathrm{3}}}\: \\ $$$$\:{k}\:=\:\mathrm{3}+\left(\mathrm{30}+\mathrm{3}\right)+\left(\mathrm{330}+\mathrm{3}\right)+......+\left(\underset{\mathrm{2019}\:\mathrm{times}} {\underbrace{\mathrm{3333}.....\mathrm{3}}0}+\mathrm{3}\right) \\ $$$$\:{k}\:=\:\underset{\mathrm{2020}\:\mathrm{3}'\mathrm{s}} {\underbrace{\mathrm{3}+\mathrm{3}+\mathrm{3}+......+\mathrm{3}}}\:+\:\mathrm{10}{j} \\ $$$$\:{k}\:=\:\underset{\mathrm{1010}\:\mathrm{times}} {\underbrace{\mathrm{6}+\mathrm{6}+\mathrm{6}+......+\mathrm{6}}}\:+\:\mathrm{10}{j} \\ $$$$\:\Rightarrow\:{k}\:\mathrm{is}\:\mathrm{an}\:\mathrm{even}\:\mathrm{number}\:\mathrm{and}\:\mathrm{therefore}\: \\ $$$$\:\:\:\:\:\:\:\mathrm{remainder}\:\mathrm{of}\:\mathrm{0}\:\mathrm{when}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{2} \\ $$$$\: \\ $$$$\: \\ $$
