Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 174581 by Gbenga last updated on 04/Aug/22

3^3^3^3 find last two digits

$$\mathrm{3}^{\mathrm{3}^{\mathrm{3}^{\mathrm{3}} } } \\ $$$$\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{last}}\:\boldsymbol{\mathrm{two}}\:\boldsymbol{\mathrm{digits}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Answered by floor(10²Eta[1]) last updated on 05/Aug/22

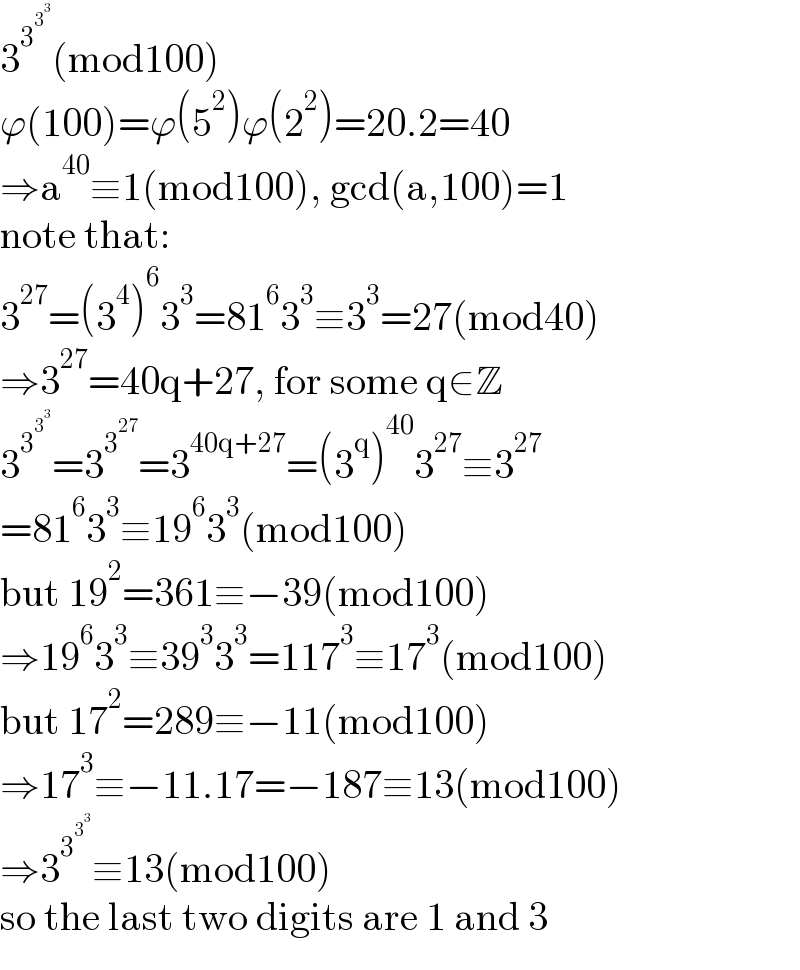
3^3^3^3 (mod100) ϕ(100)=ϕ(5^2 )ϕ(2^2 )=20.2=40 ⇒a^(40) ≡1(mod100), gcd(a,100)=1 note that: 3^(27) =(3^4 )^6 3^3 =81^6 3^3 ≡3^3 =27(mod40) ⇒3^(27) =40q+27, for some q∈Z 3^3^3^3 =3^3^(27) =3^(40q+27) =(3^q )^(40) 3^(27) ≡3^(27) =81^6 3^3 ≡19^6 3^3 (mod100) but 19^2 =361≡−39(mod100) ⇒19^6 3^3 ≡39^3 3^3 =117^3 ≡17^3 (mod100) but 17^2 =289≡−11(mod100) ⇒17^3 ≡−11.17=−187≡13(mod100) ⇒3^3^3^3 ≡13(mod100) so the last two digits are 1 and 3

$$\mathrm{3}^{\mathrm{3}^{\mathrm{3}^{\mathrm{3}} } } \left(\mathrm{mod100}\right) \\ $$$$\varphi\left(\mathrm{100}\right)=\varphi\left(\mathrm{5}^{\mathrm{2}} \right)\varphi\left(\mathrm{2}^{\mathrm{2}} \right)=\mathrm{20}.\mathrm{2}=\mathrm{40} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{40}} \equiv\mathrm{1}\left(\mathrm{mod100}\right),\:\mathrm{gcd}\left(\mathrm{a},\mathrm{100}\right)=\mathrm{1} \\ $$$$\mathrm{note}\:\mathrm{that}: \\ $$$$\mathrm{3}^{\mathrm{27}} =\left(\mathrm{3}^{\mathrm{4}} \right)^{\mathrm{6}} \mathrm{3}^{\mathrm{3}} =\mathrm{81}^{\mathrm{6}} \mathrm{3}^{\mathrm{3}} \equiv\mathrm{3}^{\mathrm{3}} =\mathrm{27}\left(\mathrm{mod40}\right) \\ $$$$\Rightarrow\mathrm{3}^{\mathrm{27}} =\mathrm{40q}+\mathrm{27},\:\mathrm{for}\:\mathrm{some}\:\mathrm{q}\in\mathbb{Z} \\ $$$$\mathrm{3}^{\mathrm{3}^{\mathrm{3}^{\mathrm{3}} } } =\mathrm{3}^{\mathrm{3}^{\mathrm{27}} } =\mathrm{3}^{\mathrm{40q}+\mathrm{27}} =\left(\mathrm{3}^{\mathrm{q}} \right)^{\mathrm{40}} \mathrm{3}^{\mathrm{27}} \equiv\mathrm{3}^{\mathrm{27}} \\ $$$$=\mathrm{81}^{\mathrm{6}} \mathrm{3}^{\mathrm{3}} \equiv\mathrm{19}^{\mathrm{6}} \mathrm{3}^{\mathrm{3}} \left(\mathrm{mod100}\right) \\ $$$$\mathrm{but}\:\mathrm{19}^{\mathrm{2}} =\mathrm{361}\equiv−\mathrm{39}\left(\mathrm{mod100}\right) \\ $$$$\Rightarrow\mathrm{19}^{\mathrm{6}} \mathrm{3}^{\mathrm{3}} \equiv\mathrm{39}^{\mathrm{3}} \mathrm{3}^{\mathrm{3}} =\mathrm{117}^{\mathrm{3}} \equiv\mathrm{17}^{\mathrm{3}} \left(\mathrm{mod100}\right) \\ $$$$\mathrm{but}\:\mathrm{17}^{\mathrm{2}} =\mathrm{289}\equiv−\mathrm{11}\left(\mathrm{mod100}\right) \\ $$$$\Rightarrow\mathrm{17}^{\mathrm{3}} \equiv−\mathrm{11}.\mathrm{17}=−\mathrm{187}\equiv\mathrm{13}\left(\mathrm{mod100}\right) \\ $$$$\Rightarrow\mathrm{3}^{\mathrm{3}^{\mathrm{3}^{\mathrm{3}} } } \equiv\mathrm{13}\left(\mathrm{mod100}\right) \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{last}\:\mathrm{two}\:\mathrm{digits}\:\mathrm{are}\:\mathrm{1}\:\mathrm{and}\:\mathrm{3} \\ $$

Commented by Gbenga last updated on 14/Aug/22

thankw wk

$$\boldsymbol{\mathrm{thankw}}\:\boldsymbol{\mathrm{wk}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com