
Question Number 155335 by mathdanisur last updated on 28/Sep/21
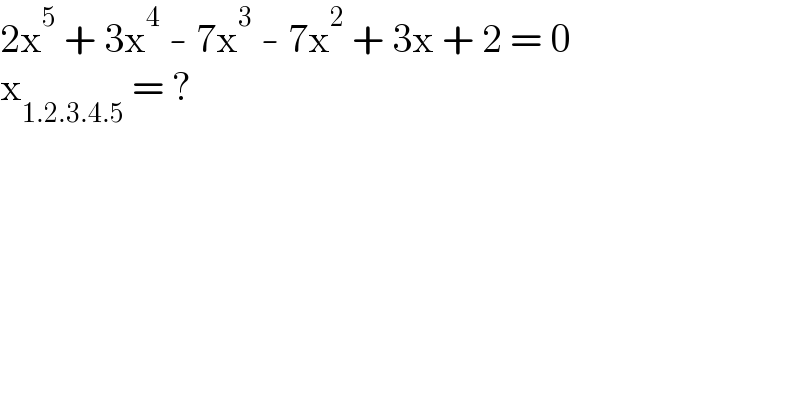
$$\mathrm{2x}^{\mathrm{5}} \:+\:\mathrm{3x}^{\mathrm{4}} \:-\:\mathrm{7x}^{\mathrm{3}} \:-\:\mathrm{7x}^{\mathrm{2}} \:+\:\mathrm{3x}\:+\:\mathrm{2}\:=\:\mathrm{0} \\ $$$$\mathrm{x}_{\mathrm{1}.\mathrm{2}.\mathrm{3}.\mathrm{4}.\mathrm{5}} \:=\:? \\ $$
Answered by MJS_new last updated on 28/Sep/21
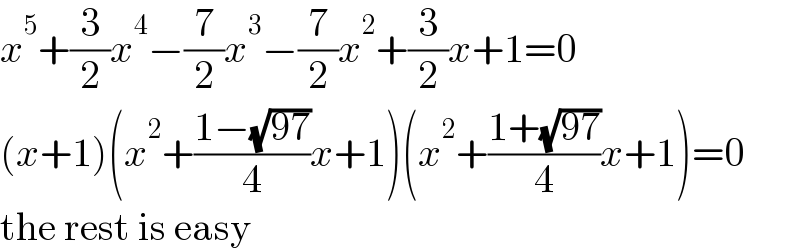
$${x}^{\mathrm{5}} +\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{4}} −\frac{\mathrm{7}}{\mathrm{2}}{x}^{\mathrm{3}} −\frac{\mathrm{7}}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\frac{\mathrm{1}−\sqrt{\mathrm{97}}}{\mathrm{4}}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\frac{\mathrm{1}+\sqrt{\mathrm{97}}}{\mathrm{4}}{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$
Commented by mathdanisur last updated on 29/Sep/21
$$\mathrm{Very}\:\mathrm{nice}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thank}\:\mathrm{you} \\ $$
