
Question Number 192928 by BaliramKumar last updated on 31/May/23
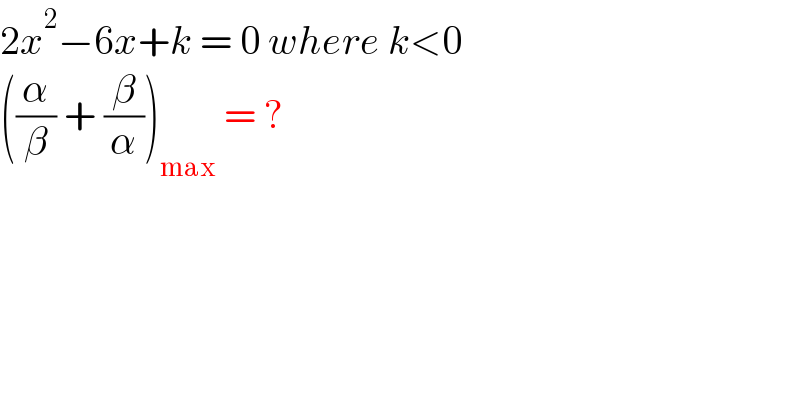
$$\mathrm{2}{x}^{\mathrm{2}} −\mathrm{6}{x}+{k}\:=\:\mathrm{0}\:{where}\:{k}<\mathrm{0}\: \\ $$$$\left(\frac{\alpha}{\beta}\:+\:\frac{\beta}{\alpha}\right)_{\mathrm{max}} \:=\:? \\ $$
Answered by MM42 last updated on 31/May/23
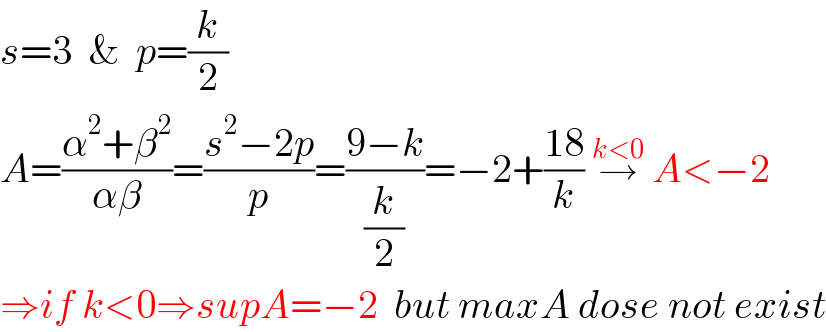
$${s}=\mathrm{3}\:\:\&\:\:{p}=\frac{{k}}{\mathrm{2}} \\ $$$${A}=\frac{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }{\alpha\beta}=\frac{{s}^{\mathrm{2}} −\mathrm{2}{p}}{{p}}=\frac{\mathrm{9}−{k}}{\frac{{k}}{\mathrm{2}}}=−\mathrm{2}+\frac{\mathrm{18}}{{k}}\:\overset{{k}<\mathrm{0}} {\rightarrow}\:{A}<−\mathrm{2} \\ $$$$\Rightarrow{if}\:{k}<\mathrm{0}\Rightarrow{supA}=−\mathrm{2}\:\:{but}\:{maxA}\:{dose}\:{not}\:{exist} \\ $$
Commented by BaliramKumar last updated on 31/May/23

$$\mathrm{thanks}\:\mathrm{Sir} \\ $$
Commented by MM42 last updated on 31/May/23

$${good}\:{luck} \\ $$
