Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 7030 by Tawakalitu. last updated on 07/Aug/16

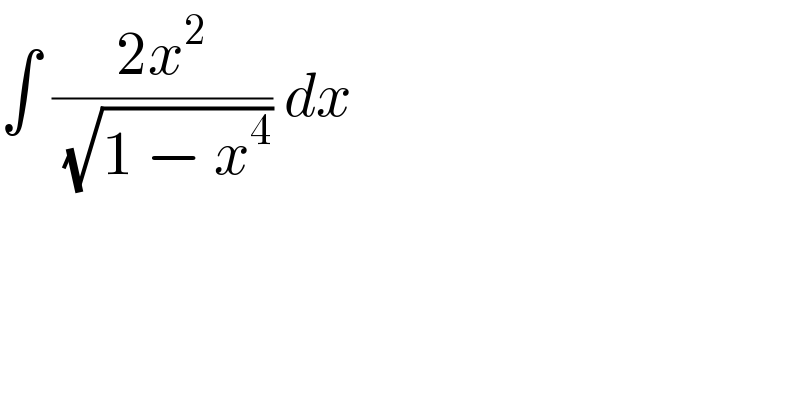
∫ ((2x^2 )/(√(1 − x^4 ))) dx

$$\int\:\frac{\mathrm{2}{x}^{\mathrm{2}} }{\sqrt{\mathrm{1}\:−\:{x}^{\mathrm{4}} }}\:{dx}\: \\ $$

Answered by uchechukwu okorie favour last updated on 10/Aug/16

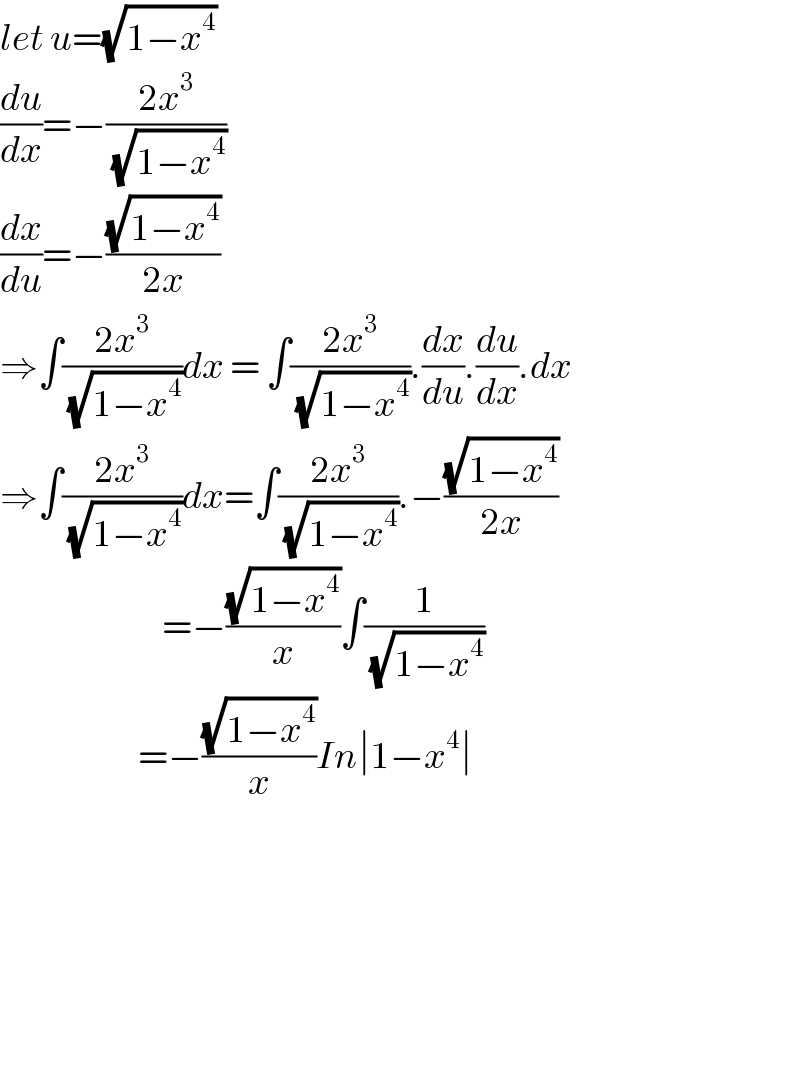
let u=(√(1−x^4 )) (du/dx)=−((2x^3 )/(√(1−x^4 ))) (dx/du)=−((√(1−x^4 ))/(2x)) ⇒∫((2x^3 )/(√(1−x^4 )))dx = ∫((2x^3 )/(√(1−x^4 ))).(dx/du).(du/dx).dx ⇒∫((2x^3 )/(√(1−x^4 )))dx=∫((2x^3 )/(√(1−x^4 ))).−((√(1−x^4 ))/(2x)) =−((√(1−x^4 ))/x)∫(1/(√(1−x^4 ))) =−((√(1−x^4 ))/x)In∣1−x^4 ∣

$${let}\:{u}=\sqrt{\mathrm{1}−{x}^{\mathrm{4}} } \\ $$$$\frac{{du}}{{dx}}=−\frac{\mathrm{2}{x}^{\mathrm{3}} }{\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }} \\ $$$$\frac{{dx}}{{du}}=−\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}{\mathrm{2}{x}} \\ $$$$\Rightarrow\int\frac{\mathrm{2}{x}^{\mathrm{3}} }{\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}{dx}\:=\:\int\frac{\mathrm{2}{x}^{\mathrm{3}} }{\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}.\frac{{dx}}{{du}}.\frac{{du}}{{dx}}.{dx} \\ $$$$\Rightarrow\int\frac{\mathrm{2}{x}^{\mathrm{3}} }{\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}{dx}=\int\frac{\mathrm{2}{x}^{\mathrm{3}} }{\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}.−\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}{\mathrm{2}{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}{{x}}\int\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}{{x}}{In}\mid\mathrm{1}−{x}^{\mathrm{4}} \mid \\ $$$$ \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com