Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 193366 by aipman last updated on 11/Jun/23

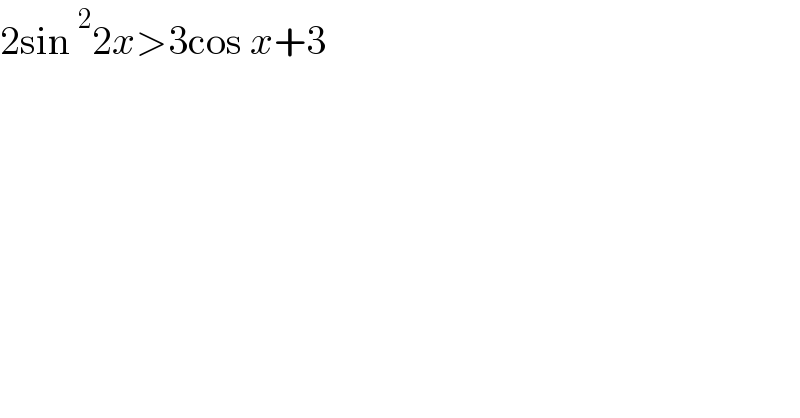
2sin^2 2x>3cos x+3

$$\mathrm{2sin}\:^{\mathrm{2}} \mathrm{2}{x}>\mathrm{3cos}\:{x}+\mathrm{3} \\ $$

Answered by Frix last updated on 11/Jun/23

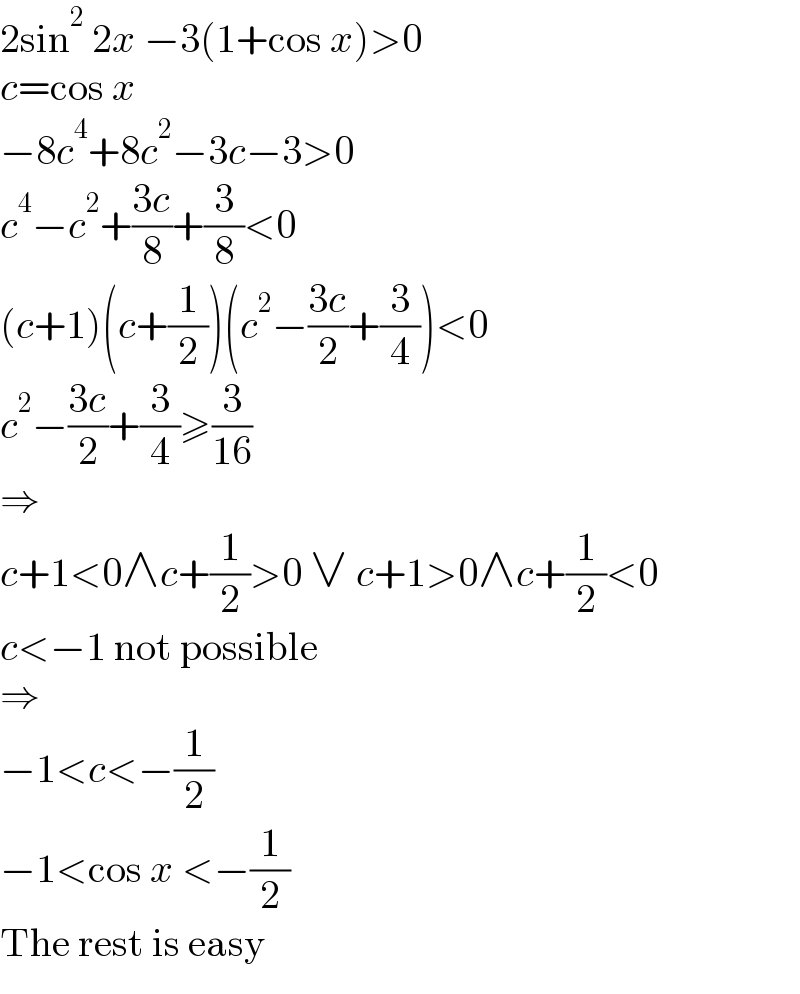
2sin^2 2x −3(1+cos x)>0 c=cos x −8c^4 +8c^2 −3c−3>0 c^4 −c^2 +((3c)/8)+(3/8)<0 (c+1)(c+(1/2))(c^2 −((3c)/2)+(3/4))<0 c^2 −((3c)/2)+(3/4)≥(3/(16)) ⇒ c+1<0∧c+(1/2)>0 ∨ c+1>0∧c+(1/2)<0 c<−1 not possible ⇒ −1<c<−(1/2) −1<cos x <−(1/2) The rest is easy

$$\mathrm{2sin}^{\mathrm{2}} \:\mathrm{2}{x}\:−\mathrm{3}\left(\mathrm{1}+\mathrm{cos}\:{x}\right)>\mathrm{0} \\ $$$${c}=\mathrm{cos}\:{x} \\ $$$$−\mathrm{8}{c}^{\mathrm{4}} +\mathrm{8}{c}^{\mathrm{2}} −\mathrm{3}{c}−\mathrm{3}>\mathrm{0} \\ $$$${c}^{\mathrm{4}} −{c}^{\mathrm{2}} +\frac{\mathrm{3}{c}}{\mathrm{8}}+\frac{\mathrm{3}}{\mathrm{8}}<\mathrm{0} \\ $$$$\left({c}+\mathrm{1}\right)\left({c}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left({c}^{\mathrm{2}} −\frac{\mathrm{3}{c}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}\right)<\mathrm{0} \\ $$$${c}^{\mathrm{2}} −\frac{\mathrm{3}{c}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}\geqslant\frac{\mathrm{3}}{\mathrm{16}} \\ $$$$\Rightarrow \\ $$$${c}+\mathrm{1}<\mathrm{0}\wedge{c}+\frac{\mathrm{1}}{\mathrm{2}}>\mathrm{0}\:\vee\:{c}+\mathrm{1}>\mathrm{0}\wedge{c}+\frac{\mathrm{1}}{\mathrm{2}}<\mathrm{0} \\ $$$${c}<−\mathrm{1}\:\mathrm{not}\:\mathrm{possible} \\ $$$$\Rightarrow \\ $$$$−\mathrm{1}<{c}<−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$−\mathrm{1}<\mathrm{cos}\:{x}\:<−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{The}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$

Commented by aipman last updated on 13/Jun/23

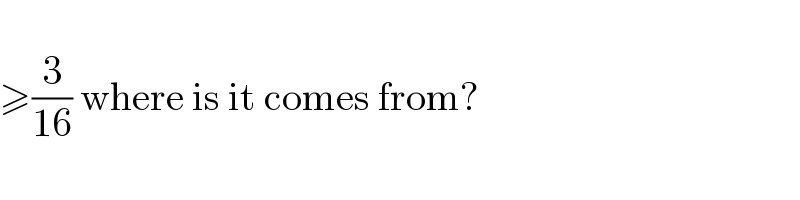
≥(3/(16)) where is it comes from?

$$ \\ $$$$\geqslant\frac{\mathrm{3}}{\mathrm{16}}\:\mathrm{where}\:\mathrm{is}\:\mathrm{it}\:\mathrm{comes}\:\mathrm{from}? \\ $$

Commented by Frix last updated on 16/Jun/23

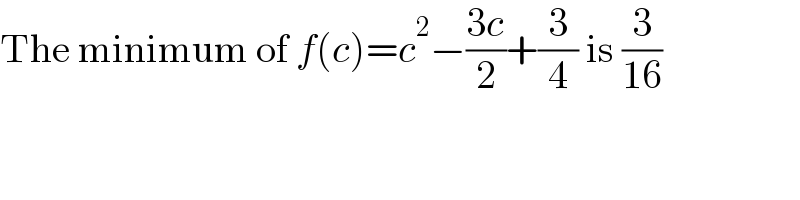
The minimum of f(c)=c^2 −((3c)/2)+(3/4) is (3/(16))

$$\mathrm{The}\:\mathrm{minimum}\:\mathrm{of}\:{f}\left({c}\right)={c}^{\mathrm{2}} −\frac{\mathrm{3}{c}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{is}\:\frac{\mathrm{3}}{\mathrm{16}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com