Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 128460 by BHOOPENDRA last updated on 07/Jan/21

2e^(3t) sin4t find laplace transformation?

$$\mathrm{2}{e}^{\mathrm{3}{t}} {sin}\mathrm{4}{t}\: \\ $$$${find}\:{laplace}\:{transformation}? \\ $$

Answered by Dwaipayan Shikari last updated on 07/Jan/21

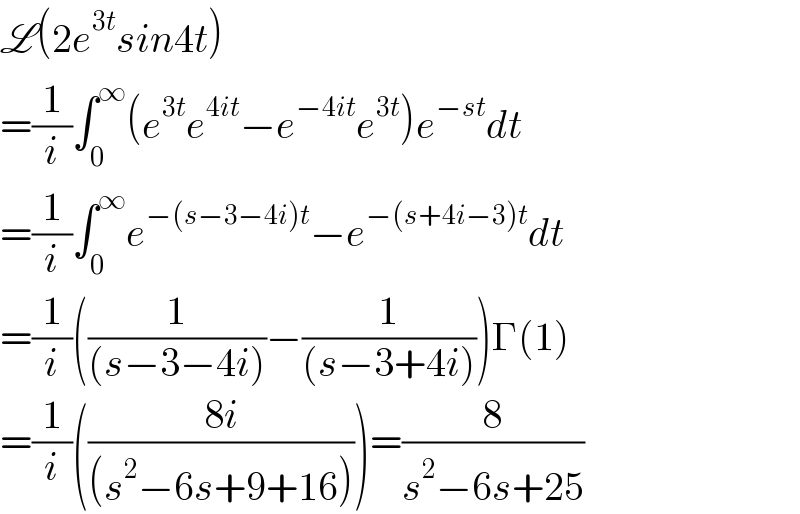
L(2e^(3t) sin4t) =(1/i)∫_0 ^∞ (e^(3t) e^(4it) −e^(−4it) e^(3t) )e^(−st) dt =(1/i)∫_0 ^∞ e^(−(s−3−4i)t) −e^(−(s+4i−3)t) dt =(1/i)((1/((s−3−4i)))−(1/((s−3+4i))))Γ(1) =(1/i)(((8i)/((s^2 −6s+9+16))))=(8/(s^2 −6s+25))

$$\mathscr{L}\left(\mathrm{2}{e}^{\mathrm{3}{t}} {sin}\mathrm{4}{t}\right) \\ $$$$=\frac{\mathrm{1}}{{i}}\int_{\mathrm{0}} ^{\infty} \left({e}^{\mathrm{3}{t}} {e}^{\mathrm{4}{it}} −{e}^{−\mathrm{4}{it}} {e}^{\mathrm{3}{t}} \right){e}^{−{st}} {dt} \\ $$$$=\frac{\mathrm{1}}{{i}}\int_{\mathrm{0}} ^{\infty} {e}^{−\left({s}−\mathrm{3}−\mathrm{4}{i}\right){t}} −{e}^{−\left({s}+\mathrm{4}{i}−\mathrm{3}\right){t}} {dt} \\ $$$$=\frac{\mathrm{1}}{{i}}\left(\frac{\mathrm{1}}{\left({s}−\mathrm{3}−\mathrm{4}{i}\right)}−\frac{\mathrm{1}}{\left({s}−\mathrm{3}+\mathrm{4}{i}\right)}\right)\Gamma\left(\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{{i}}\left(\frac{\mathrm{8}{i}}{\left({s}^{\mathrm{2}} −\mathrm{6}{s}+\mathrm{9}+\mathrm{16}\right)}\right)=\frac{\mathrm{8}}{{s}^{\mathrm{2}} −\mathrm{6}{s}+\mathrm{25}} \\ $$

Commented by BHOOPENDRA last updated on 07/Jan/21

tsinh2tsin3t plz help me out this n thanks for this solution

$${tsinh}\mathrm{2}{tsin}\mathrm{3}{t} \\ $$$${plz}\:{help}\:{me}\:{out}\:{this}\: \\ $$$${n}\:{thanks}\:{for}\:{this}\:{solution} \\ $$

Answered by mnjuly1970 last updated on 07/Jan/21

solution: L [f(t)]=F (s) L [e^(at) f(t)]=F(s−a).... L [2e^(3t) sin(4t)]=2∗(4/((s−3)^2 +16)) =(8/(s^2 −6s+25))

$${solution}: \\ $$$$\mathscr{L}\:\left[{f}\left({t}\right)\right]={F}\:\left({s}\right) \\ $$$$\:\:\mathscr{L}\:\left[{e}^{{at}} {f}\left({t}\right)\right]={F}\left({s}−{a}\right).... \\ $$$$\mathscr{L}\:\left[\mathrm{2}{e}^{\mathrm{3}{t}} {sin}\left(\mathrm{4}{t}\right)\right]=\mathrm{2}\ast\frac{\mathrm{4}}{\left({s}−\mathrm{3}\right)^{\mathrm{2}} +\mathrm{16}} \\ $$$$\:\:\:=\frac{\mathrm{8}}{{s}^{\mathrm{2}} −\mathrm{6}{s}+\mathrm{25}} \\ $$

Commented by BHOOPENDRA last updated on 07/Jan/21

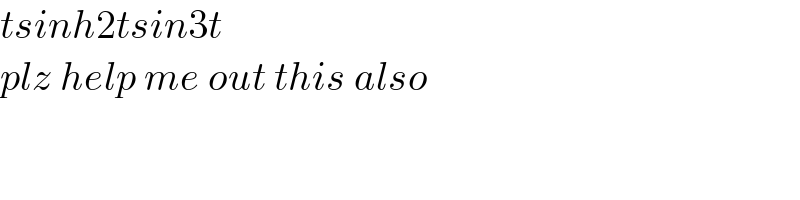
tsinh2tsin3t plz help me out this also

$${tsinh}\mathrm{2}{tsin}\mathrm{3}{t}\: \\ $$$${plz}\:{help}\:{me}\:{out}\:{this}\:{also} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com