
Question Number 21701 by Isse last updated on 01/Oct/17

$$\int\mathrm{2}{cot}^{\mathrm{2}} \mathrm{2}{t} \\ $$
Commented by Tikufly last updated on 01/Oct/17
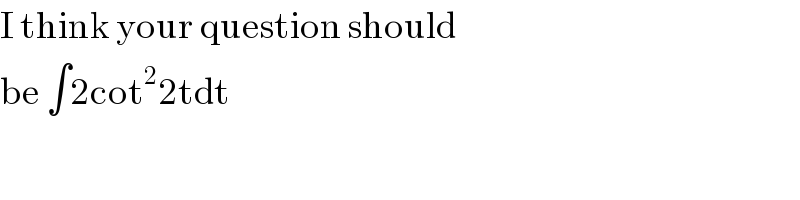
$$\mathrm{I}\:\mathrm{think}\:\mathrm{your}\:\mathrm{question}\:\mathrm{should} \\ $$$$\mathrm{be}\:\int\mathrm{2cot}^{\mathrm{2}} \mathrm{2tdt} \\ $$
Answered by alex041103 last updated on 01/Oct/17

$$\int\mathrm{2}{cot}^{\mathrm{2}} \left(\mathrm{2}{t}\right){dt} \\ $$$${We}\:{make}\:{the}\:{substitution} \\ $$$${u}=\mathrm{2}{t},\:{du}=\mathrm{2}{dt} \\ $$$$\int\mathrm{2}{cot}^{\mathrm{2}} \left(\mathrm{2}{t}\right){dt}=\int{cot}^{\mathrm{2}} \left({u}\right){du}= \\ $$$$=\int\:\frac{{cos}^{\mathrm{2}} {u}}{{sin}^{\mathrm{2}} {u}}{du}=\int{cosu}\:\frac{{cosu}}{{sin}^{\mathrm{2}} {u}}\:{du}={I} \\ $$$${Now}\:{we}\:{integrate}\:{by}\:{parts} \\ $$$${x}={cosu}\:\:\:\:{dv}=\frac{{cosu}}{{sin}^{\mathrm{2}} {u}}{du} \\ $$$${dx}=−{sinu}\:{du}\:\:\:{v}=−\frac{\mathrm{1}}{{sinu}} \\ $$$$\Rightarrow{I}=−\frac{{cosu}}{{sinu}}−\int\:{du}=−{cot}\left({u}\right)−{u}= \\ $$$$=−{cot}\left(\mathrm{2}{t}\right)−\mathrm{2}{t}+{C} \\ $$$${Ans}.\:\int\mathrm{2}{cot}^{\mathrm{2}} \left(\mathrm{2}{t}\right)\:{dt}=−{cot}\left(\mathrm{2}{t}\right)−\mathrm{2}{t}+{C} \\ $$
Answered by Tikufly last updated on 01/Oct/17
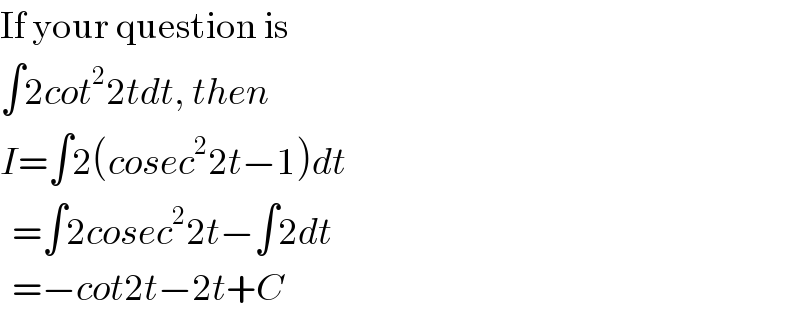
$$\mathrm{If}\:\mathrm{your}\:\mathrm{question}\:\mathrm{is} \\ $$$$\int\mathrm{2}{cot}^{\mathrm{2}} \mathrm{2}{tdt},\:{then} \\ $$$${I}=\int\mathrm{2}\left({cosec}^{\mathrm{2}} \mathrm{2}{t}−\mathrm{1}\right){dt} \\ $$$$\:\:=\int\mathrm{2}{cosec}^{\mathrm{2}} \mathrm{2}{t}−\int\mathrm{2}{dt} \\ $$$$\:\:=−{cot}\mathrm{2}{t}−\mathrm{2}{t}+{C} \\ $$
Commented by Isse last updated on 01/Oct/17

$${thnks} \\ $$
