
Question Number 29909 by *D¬ B£$T* last updated on 13/Feb/18
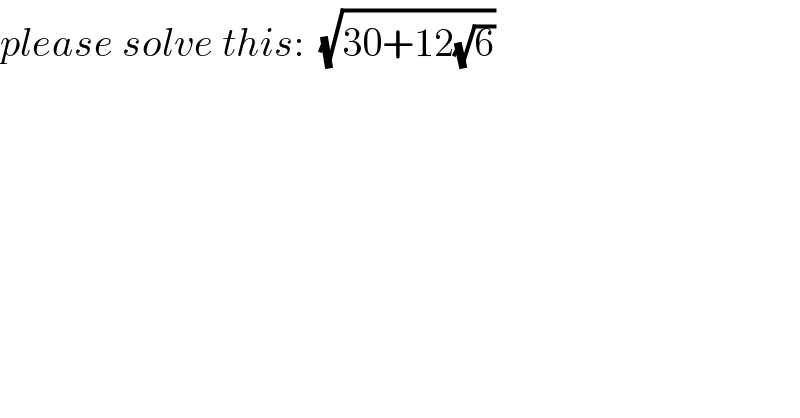
$${please}\:{solve}\:{this}:\:\:\sqrt{\mathrm{30}+\mathrm{12}\sqrt{\mathrm{6}}} \\ $$
Commented by rahul 19 last updated on 13/Feb/18
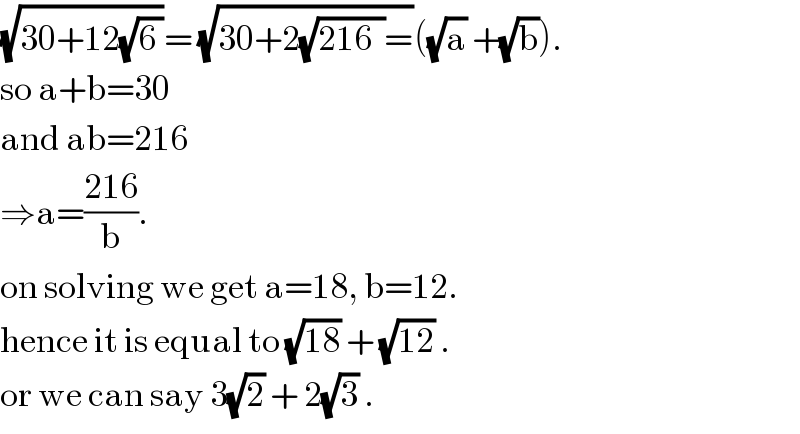
$$\sqrt{\mathrm{30}+\mathrm{12}\sqrt{\mathrm{6}\:}}=\:\sqrt{\mathrm{30}+\mathrm{2}\sqrt{\mathrm{216}\:\:}=}\left(\sqrt{\mathrm{a}}\:+\sqrt{\mathrm{b}}\right). \\ $$$$\mathrm{so}\:\mathrm{a}+\mathrm{b}=\mathrm{30} \\ $$$$\mathrm{and}\:\mathrm{ab}=\mathrm{216} \\ $$$$\Rightarrow\mathrm{a}=\frac{\mathrm{216}}{\mathrm{b}}. \\ $$$$\mathrm{on}\:\mathrm{solving}\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}=\mathrm{18},\:\mathrm{b}=\mathrm{12}. \\ $$$$\mathrm{hence}\:\mathrm{it}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\sqrt{\mathrm{18}}\:+\:\sqrt{\mathrm{12}}\:. \\ $$$$\mathrm{or}\:\mathrm{we}\:\mathrm{can}\:\mathrm{say}\:\mathrm{3}\sqrt{\mathrm{2}}\:+\:\mathrm{2}\sqrt{\mathrm{3}}\:. \\ $$
Answered by mrW2 last updated on 13/Feb/18

$${let}\:\mathrm{30}+\mathrm{12}\sqrt{\mathrm{6}}=\left({p}+{q}\sqrt{\mathrm{6}}\right)^{\mathrm{2}} ={p}^{\mathrm{2}} +\mathrm{2}{pq}\sqrt{\mathrm{6}}+\mathrm{6}{q}^{\mathrm{2}} \\ $$$$\mathrm{2}{pq}=\mathrm{12}\Rightarrow{pq}=\mathrm{6} \\ $$$${p}^{\mathrm{2}} +\mathrm{6}{q}^{\mathrm{2}} =\mathrm{30} \\ $$$$\Rightarrow{p}^{\mathrm{2}} +\mathrm{6}\left(\frac{\mathrm{6}}{{p}}\right)^{\mathrm{2}} =\mathrm{30} \\ $$$$\Rightarrow{p}^{\mathrm{4}} −\mathrm{30}{p}^{\mathrm{2}} +\mathrm{216}=\mathrm{0} \\ $$$$\Rightarrow{p}^{\mathrm{2}} =\frac{\mathrm{30}\pm\sqrt{\mathrm{30}^{\mathrm{2}} −\mathrm{4}×\mathrm{216}}}{\mathrm{2}}=\frac{\mathrm{30}\pm\mathrm{6}}{\mathrm{2}}=\begin{cases}{\mathrm{18}}\\{\mathrm{12}}\end{cases} \\ $$$$\Rightarrow{p}=\begin{cases}{\mathrm{3}\sqrt{\mathrm{2}}}\\{\mathrm{2}\sqrt{\mathrm{3}}}\end{cases} \\ $$$$\Rightarrow{q}=\begin{cases}{\frac{\mathrm{6}}{\mathrm{3}\sqrt{\mathrm{2}}}=\sqrt{\mathrm{2}}}\\{\frac{\mathrm{6}}{\mathrm{2}\sqrt{\mathrm{3}}}=\sqrt{\mathrm{3}}}\end{cases} \\ $$$$\Rightarrow\sqrt{\mathrm{30}+\mathrm{12}\sqrt{\mathrm{6}}}={p}+{q}\sqrt{\mathrm{6}}=\mathrm{3}\sqrt{\mathrm{2}}+\sqrt{\mathrm{2}}×\sqrt{\mathrm{6}}=\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}} \\ $$$${or} \\ $$$$\Rightarrow\sqrt{\mathrm{30}+\mathrm{12}\sqrt{\mathrm{6}}}=\mathrm{2}\sqrt{\mathrm{3}}+\sqrt{\mathrm{3}}×\sqrt{\mathrm{6}}=\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{3}\sqrt{\mathrm{2}}={the}\:{same}\:{as}\:{abov} \\ $$
Commented by NECx last updated on 13/Feb/18

$${so}\:{nice}\:{workings} \\ $$
Answered by ajfour last updated on 13/Feb/18
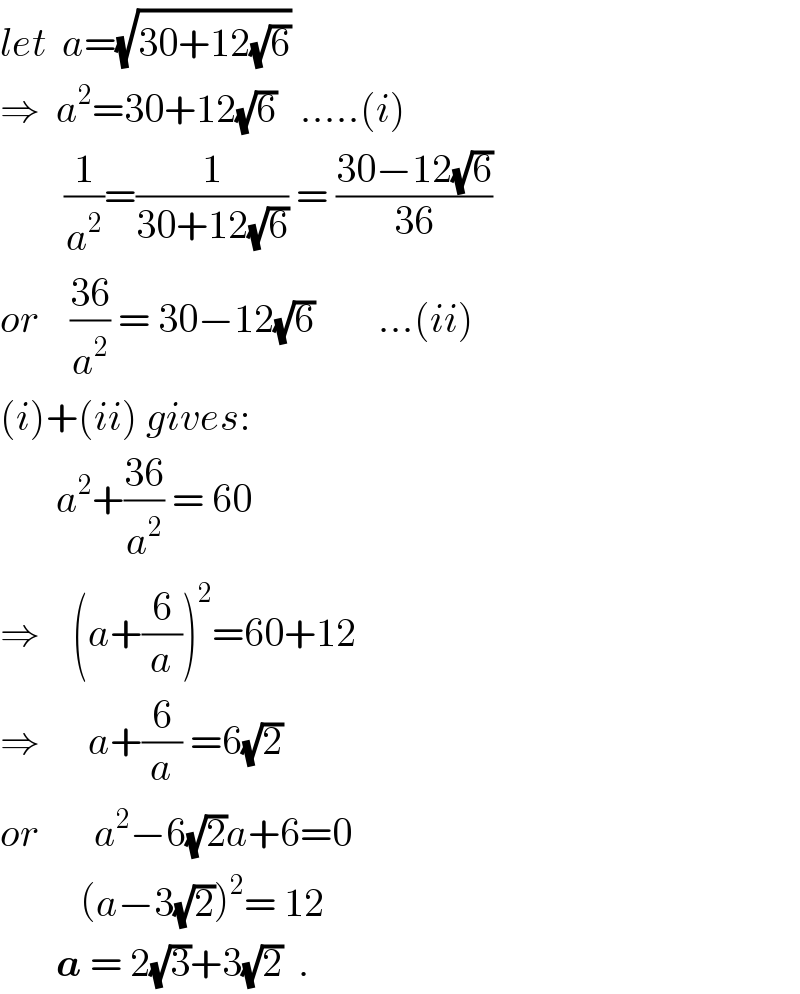
$${let}\:\:{a}=\sqrt{\mathrm{30}+\mathrm{12}\sqrt{\mathrm{6}}} \\ $$$$\Rightarrow\:\:{a}^{\mathrm{2}} =\mathrm{30}+\mathrm{12}\sqrt{\mathrm{6}}\:\:\:.....\left({i}\right) \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{30}+\mathrm{12}\sqrt{\mathrm{6}}}\:=\:\frac{\mathrm{30}−\mathrm{12}\sqrt{\mathrm{6}}}{\mathrm{36}} \\ $$$${or}\:\:\:\:\frac{\mathrm{36}}{{a}^{\mathrm{2}} }\:=\:\mathrm{30}−\mathrm{12}\sqrt{\mathrm{6}}\:\:\:\:\:\:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right)\:{gives}: \\ $$$$\:\:\:\:\:\:\:{a}^{\mathrm{2}} +\frac{\mathrm{36}}{{a}^{\mathrm{2}} }\:=\:\mathrm{60} \\ $$$$\Rightarrow\:\:\:\:\left({a}+\frac{\mathrm{6}}{{a}}\right)^{\mathrm{2}} =\mathrm{60}+\mathrm{12}\: \\ $$$$\Rightarrow\:\:\:\:\:\:{a}+\frac{\mathrm{6}}{{a}}\:=\mathrm{6}\sqrt{\mathrm{2}} \\ $$$${or}\:\:\:\:\:\:\:{a}^{\mathrm{2}} −\mathrm{6}\sqrt{\mathrm{2}}{a}+\mathrm{6}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left({a}−\mathrm{3}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} =\:\mathrm{12} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{{a}}\:=\:\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{3}\sqrt{\mathrm{2}}\:\:. \\ $$
Commented by 33 last updated on 13/Feb/18
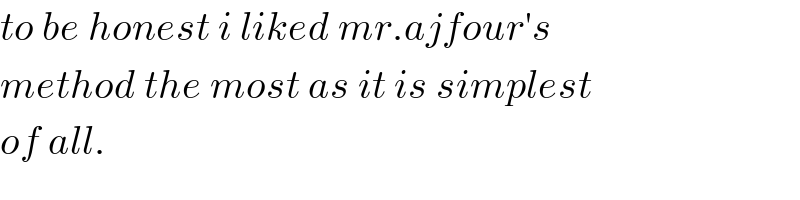
$${to}\:{be}\:{honest}\:{i}\:{liked}\:{mr}.{ajfour}'{s} \\ $$$${method}\:{the}\:{most}\:{as}\:{it}\:{is}\:{simplest} \\ $$$${of}\:{all}. \\ $$
Commented by abdo imad last updated on 13/Feb/18
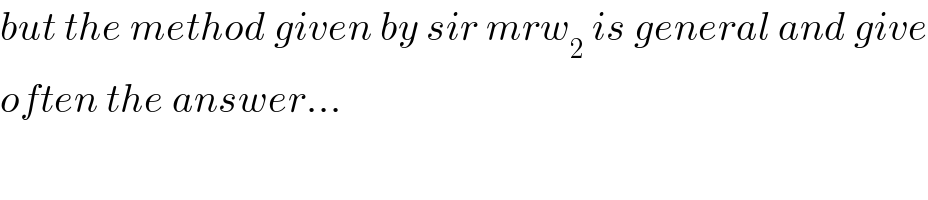
$${but}\:{the}\:{method}\:{given}\:{by}\:{sir}\:{mrw}_{\mathrm{2}} \:{is}\:{general}\:{and}\:{give} \\ $$$${often}\:{the}\:{answer}... \\ $$
Commented by 33 last updated on 13/Feb/18

$${hmmm}\:{alright} \\ $$
Commented by mrW2 last updated on 14/Feb/18
Variety is always good! All roads lead to Rome.
Commented by 33 last updated on 14/Feb/18

$${haha}\:{yeah} \\ $$
