
Question Number 29805 by mrW2 last updated on 12/Feb/18
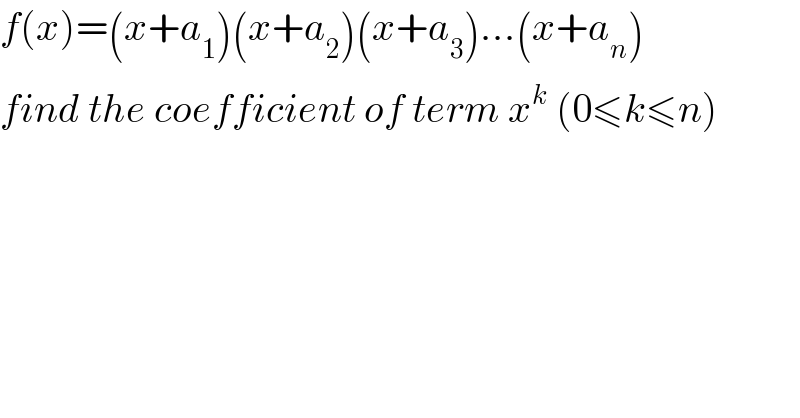
$${f}\left({x}\right)=\left({x}+{a}_{\mathrm{1}} \right)\left({x}+{a}_{\mathrm{2}} \right)\left({x}+{a}_{\mathrm{3}} \right)...\left({x}+{a}_{{n}} \right) \\ $$$${find}\:{the}\:{coefficient}\:{of}\:{term}\:{x}^{{k}} \:\left(\mathrm{0}\leqslant{k}\leqslant{n}\right) \\ $$
Commented by mrW2 last updated on 13/Feb/18

$${A}\:{first}\:{try}: \\ $$$$ \\ $$$${let}\:{P}={a}_{\mathrm{1}} {a}_{\mathrm{2}} ...{a}_{{n}} \\ $$$${let}\:{C}_{{k}} ={coefficient}\:{of}\:{term}\:{x}^{{k}} \:{in}\:{f}\left({x}\right) \\ $$$$ \\ $$$${C}_{\mathrm{0}} ={P} \\ $$$${C}_{\mathrm{1}} =\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{P}}{{a}_{{i}} }\:=\underset{{p}_{\mathrm{1}} =\mathrm{1}} {\overset{{n}} {\sum}}\:\:\underset{{p}_{\mathrm{2}} ={p}_{\mathrm{1}} +\mathrm{1}} {\overset{{n}} {\sum}}...\:\:\underset{{p}_{{n}−\mathrm{1}} ={p}_{{n}−\mathrm{2}} +\mathrm{1}} {\overset{{n}} {\sum}}\:{a}_{{p}_{\mathrm{1}} } {a}_{{p}_{\mathrm{2}} } ...{a}_{{p}_{{n}−\mathrm{1}} } \\ $$$${C}_{\mathrm{2}} =\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\:\underset{{j}={i}+\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{{P}}{{a}_{{i}} {a}_{{j}} }\:=\underset{{p}_{\mathrm{1}} =\mathrm{1}} {\overset{{n}} {\sum}}\:\:\underset{{p}_{\mathrm{2}} ={p}_{\mathrm{1}} +\mathrm{1}} {\overset{{n}} {\sum}}...\:\:\underset{{p}_{{n}−\mathrm{2}} ={p}_{{n}−\mathrm{3}} +\mathrm{1}} {\overset{{n}} {\sum}}\:{a}_{{p}_{\mathrm{1}} } {a}_{{p}_{\mathrm{2}} } ...{a}_{{p}_{{n}−\mathrm{2}} } \\ $$$$...... \\ $$$${C}_{{k}} =\underset{{p}_{\mathrm{1}} =\mathrm{1}} {\overset{{n}} {\sum}}\:\:\underset{{p}_{\mathrm{2}} ={p}_{\mathrm{1}} +\mathrm{1}} {\overset{{n}} {\sum}}...\:\:\underset{{p}_{{k}} ={p}_{{k}−\mathrm{1}} +\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{{P}}{{a}_{{p}_{\mathrm{1}} } {a}_{{p}_{\mathrm{2}} } ...{a}_{{p}_{{k}} } }\:=\underset{{p}_{\mathrm{1}} =\mathrm{1}} {\overset{{n}} {\sum}}\:\:\underset{{p}_{\mathrm{2}} ={p}_{\mathrm{1}} +\mathrm{1}} {\overset{{n}} {\sum}}...\:\:\underset{{p}_{{n}−{k}} ={p}_{{n}−{k}−\mathrm{1}} +\mathrm{1}} {\overset{{n}} {\sum}}\:{a}_{{p}_{\mathrm{1}} } {a}_{{p}_{\mathrm{2}} } ...{a}_{{p}_{{n}−{k}} } \\ $$$$\left(\mathrm{1}\leqslant{k}\leqslant{n}\right) \\ $$$$...... \\ $$$${C}_{{n}−\mathrm{1}} =\underset{{p}_{\mathrm{1}} =\mathrm{1}} {\overset{{n}} {\sum}}\:\:\underset{{p}_{\mathrm{2}} ={p}_{\mathrm{1}} +\mathrm{1}} {\overset{{n}} {\sum}}...\:\:\underset{{p}_{{n}−\mathrm{1}} ={p}_{{n}−\mathrm{2}} +\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{{P}}{{a}_{{p}_{\mathrm{1}} } {a}_{{p}_{\mathrm{2}} } ...{a}_{{p}_{{n}−\mathrm{1}} } }=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} \\ $$$${C}_{{n}} =\mathrm{1} \\ $$
