
Question Number 29184 by ANTARESVY last updated on 05/Feb/18

$$\begin{cases}{\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{4}\boldsymbol{\mathrm{xy}}}+\sqrt{\boldsymbol{\mathrm{y}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mathrm{xy}}+\mathrm{9}}=\mathrm{10}}\\{\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{y}}=\mathrm{7}}\end{cases} \\ $$$$\boldsymbol{\mathrm{How}}\:\boldsymbol{\mathrm{many}}\:\:\boldsymbol{\mathrm{real}}\:\boldsymbol{\mathrm{roots}}\:\boldsymbol{\mathrm{of}}\: \\ $$$$\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{equtions}}\:\boldsymbol{\mathrm{system}}? \\ $$
Answered by mrW2 last updated on 05/Feb/18
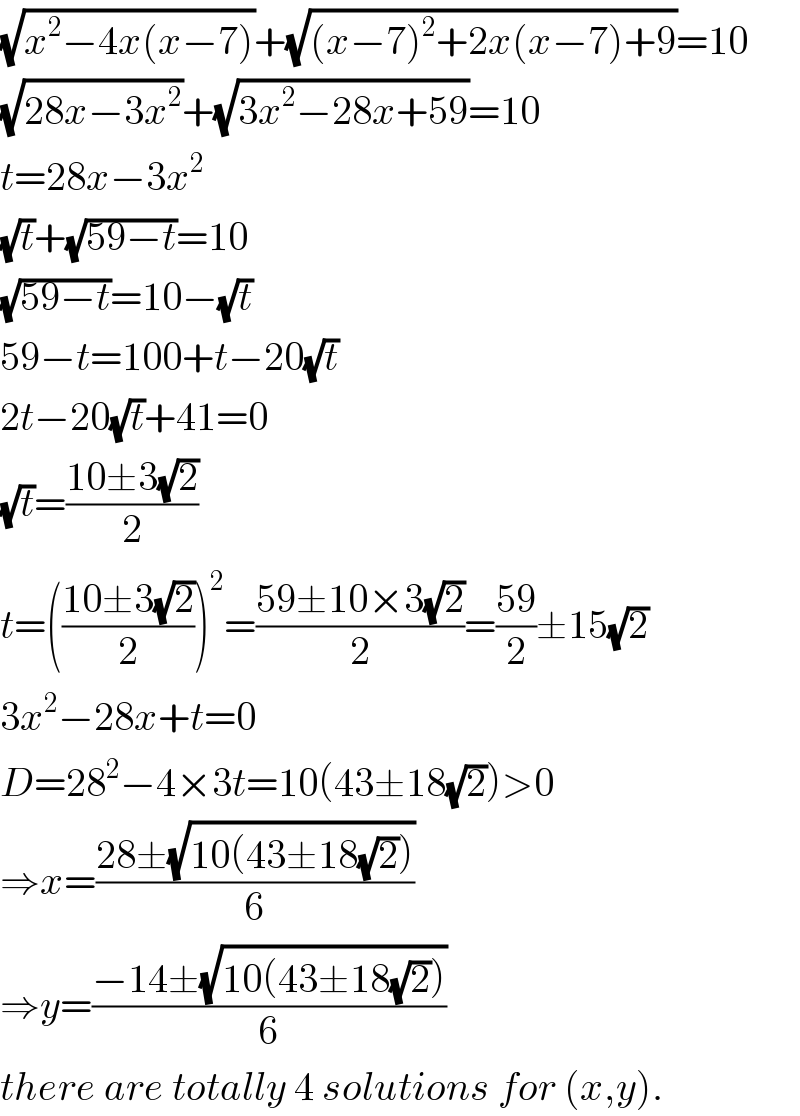
$$\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}\left({x}−\mathrm{7}\right)}+\sqrt{\left({x}−\mathrm{7}\right)^{\mathrm{2}} +\mathrm{2}{x}\left({x}−\mathrm{7}\right)+\mathrm{9}}=\mathrm{10} \\ $$$$\sqrt{\mathrm{28}{x}−\mathrm{3}{x}^{\mathrm{2}} }+\sqrt{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{28}{x}+\mathrm{59}}=\mathrm{10} \\ $$$${t}=\mathrm{28}{x}−\mathrm{3}{x}^{\mathrm{2}} \\ $$$$\sqrt{{t}}+\sqrt{\mathrm{59}−{t}}=\mathrm{10} \\ $$$$\sqrt{\mathrm{59}−{t}}=\mathrm{10}−\sqrt{{t}} \\ $$$$\mathrm{59}−{t}=\mathrm{100}+{t}−\mathrm{20}\sqrt{{t}} \\ $$$$\mathrm{2}{t}−\mathrm{20}\sqrt{{t}}+\mathrm{41}=\mathrm{0} \\ $$$$\sqrt{{t}}=\frac{\mathrm{10}\pm\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${t}=\left(\frac{\mathrm{10}\pm\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{59}\pm\mathrm{10}×\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{2}}=\frac{\mathrm{59}}{\mathrm{2}}\pm\mathrm{15}\sqrt{\mathrm{2}} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{28}{x}+{t}=\mathrm{0} \\ $$$${D}=\mathrm{28}^{\mathrm{2}} −\mathrm{4}×\mathrm{3}{t}=\mathrm{10}\left(\mathrm{43}\pm\mathrm{18}\sqrt{\mathrm{2}}\right)>\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{28}\pm\sqrt{\mathrm{10}\left(\mathrm{43}\pm\mathrm{18}\sqrt{\mathrm{2}}\right)}}{\mathrm{6}} \\ $$$$\Rightarrow{y}=\frac{−\mathrm{14}\pm\sqrt{\mathrm{10}\left(\mathrm{43}\pm\mathrm{18}\sqrt{\mathrm{2}}\right)}}{\mathrm{6}} \\ $$$${there}\:{are}\:{totally}\:\mathrm{4}\:{solutions}\:{for}\:\left({x},{y}\right). \\ $$
Commented by NECx last updated on 05/Feb/18
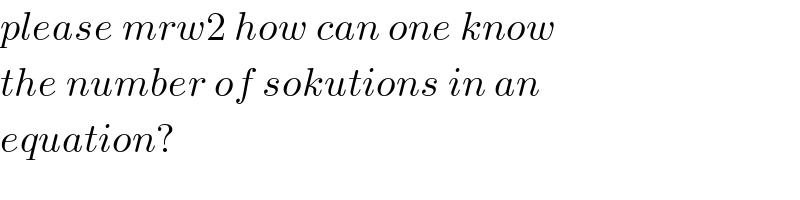
$${please}\:{mrw}\mathrm{2}\:{how}\:{can}\:{one}\:{know} \\ $$$${the}\:{number}\:{of}\:{sokutions}\:{in}\:{an} \\ $$$${equation}? \\ $$
Commented by mrW2 last updated on 05/Feb/18

$${I}\:{think}\:{there}\:{is}\:{no}\:{general}\:{method}. \\ $$$${Just}\:{try}\:{to}\:{find}\:{the}\:{solutions}. \\ $$
