
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 28015 by ajfour last updated on 18/Jan/18
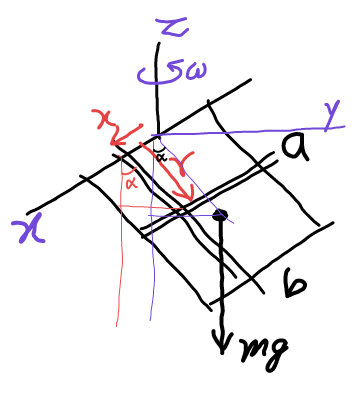
Commented by ajfour last updated on 18/Jan/18

$${Q}.\mathrm{27997}\:{solution} \\ $$
Answered by ajfour last updated on 18/Jan/18
![L^� =(−I_(xz) i^� −I_(yz) j^� +I_z k^� )ω since ω_x =ω_y =0 , ω_z =ω 𝛕^� =−[mg((a/2))sin α]i^� with 𝛂^� =0, 𝛕^� = 𝛚^� ×L^� =(ωk^� )×(−I_(xz) i^� −I_(yz) j^� +I_z k^� )ω =(−I_(xz) j^� +I_(yz) i^� )ω^2 I_(xz) =∫xz dm =(m/(ab))∫_0 ^( a) ∫_(−b/2) ^( +b/2) x(−rcos α)dx dr =(m/(ab))∫_0 ^( a) ∫_(−b/2) ^( +b/2) x(−rcos α)dx dr =0 I_(yz) =∫yz dm =(m/(ab))∫_(−b/2) ^( +b/2) ∫_0 ^( a) (rsin α)(−rcos α)dr dx =(m/(ab))(−((ba^3 )/3))sin α cos α with 𝛕^� = 𝛚^� ×L^� , we arrive at −mg((a/2))sin α=(m/(ab))(−((ba^3 )/3))ω^2 sin α cos α ⇒ ω = (√((3g)/(2acos α))) .](Q28021.png)
$$\bar {\boldsymbol{{L}}}=\left(−{I}_{{xz}} \hat {{i}}−{I}_{{yz}} \hat {{j}}+{I}_{{z}} \hat {{k}}\right)\omega \\ $$$${since}\:\omega_{{x}} =\omega_{{y}} =\mathrm{0}\:,\:\omega_{{z}} =\omega \\ $$$$\bar {\boldsymbol{\tau}}\:=−\left[{mg}\left(\frac{{a}}{\mathrm{2}}\right)\mathrm{sin}\:\alpha\right]\hat {{i}} \\ $$$${with}\:\:\bar {\boldsymbol{\alpha}}=\mathrm{0}, \\ $$$$\bar {\boldsymbol{\tau}}\:=\:\bar {\boldsymbol{\omega}}×\bar {\boldsymbol{{L}}} \\ $$$$\:\:\:\:=\left(\omega\hat {{k}}\right)×\left(−{I}_{{xz}} \hat {{i}}−{I}_{{yz}} \hat {{j}}+{I}_{{z}} \hat {{k}}\right)\omega \\ $$$$\:\:\:=\left(−{I}_{{xz}} \hat {{j}}+{I}_{{yz}} \hat {{i}}\right)\omega^{\mathrm{2}} \\ $$$${I}_{{xz}} =\int{xz}\:{dm}\:=\frac{{m}}{{ab}}\int_{\mathrm{0}} ^{\:\:{a}} \int_{−{b}/\mathrm{2}} ^{\:\:+{b}/\mathrm{2}} {x}\left(−{r}\mathrm{cos}\:\alpha\right){dx}\:{dr} \\ $$$$\:\:=\frac{{m}}{{ab}}\int_{\mathrm{0}} ^{\:\:{a}} \int_{−{b}/\mathrm{2}} ^{\:\:+{b}/\mathrm{2}} {x}\left(−{r}\mathrm{cos}\:\alpha\right){dx}\:{dr}\:=\mathrm{0} \\ $$$${I}_{{yz}} =\int{yz}\:{dm} \\ $$$$\:\:\:\:\:=\frac{{m}}{{ab}}\int_{−{b}/\mathrm{2}} ^{\:\:+{b}/\mathrm{2}} \int_{\mathrm{0}} ^{\:\:{a}} \left({r}\mathrm{sin}\:\alpha\right)\left(−{r}\mathrm{cos}\:\alpha\right){dr}\:{dx} \\ $$$$\:\:\:=\frac{{m}}{{ab}}\left(−\frac{{ba}^{\mathrm{3}} }{\mathrm{3}}\right)\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha \\ $$$${with}\:\:\:\bar {\boldsymbol{\tau}}\:=\:\bar {\boldsymbol{\omega}}×\bar {\boldsymbol{{L}}}\:,\:{we}\:{arrive}\:{at} \\ $$$$\:−{mg}\left(\frac{{a}}{\mathrm{2}}\right)\mathrm{sin}\:\alpha=\frac{{m}}{{ab}}\left(−\frac{{ba}^{\mathrm{3}} }{\mathrm{3}}\right)\omega^{\mathrm{2}} \mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha \\ $$$$\Rightarrow\:\:\omega\:=\:\sqrt{\frac{\mathrm{3}{g}}{\mathrm{2}{a}\mathrm{cos}\:\alpha}}\:. \\ $$$$ \\ $$
Commented by mrW2 last updated on 18/Jan/18
fine way!
