
Question Number 27974 by abdo imad last updated on 18/Jan/18
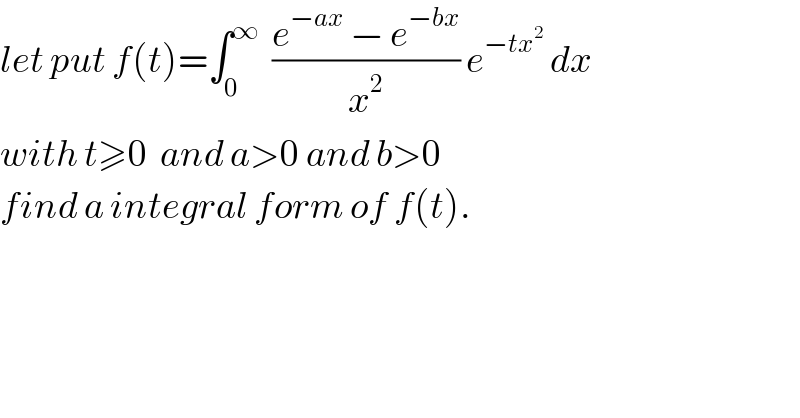
$${let}\:{put}\:{f}\left({t}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{ax}} \:−\:{e}^{−{bx}} }{{x}^{\mathrm{2}} }\:{e}^{−{tx}^{\mathrm{2}} } \:{dx} \\ $$ $${with}\:{t}\geqslant\mathrm{0}\:\:{and}\:{a}>\mathrm{0}\:{and}\:{b}>\mathrm{0} \\ $$ $${find}\:{a}\:{integral}\:{form}\:{of}\:{f}\left({t}\right). \\ $$
Commented byabdo imad last updated on 20/Jan/18
![after verifying that f is derivable on ]0,+∞[ we have f^, (t)= −∫_0 ^∞ ( e^(−ax) −e^(−bx) )e^(−tx^2 ) dx =∫_0 ^∞ e^(−tx^2 −bx) dx −∫_0 ^∞ e^(−tx^2 −ax) dx but ∫_0 ^∞ e^(−tx^2 −ax) dx = ∫_0 ^∞ e^(−( ((√t)x)^2 +2(a/(2(√t)))((√t)x) + (a^2 /(4t)) −(a^2 /(4t)))) dx = e^(a^2 /(4t)) ∫_0 ^∞ e^(−((√t)x +(a/(√t)))^2 ) dx the ch. (√t)x +(a/(√t))=u give ∫_0 ^∞ e^(−tx^2 −ax) dx = e^(a^2 /(4t)) ∫_(a/(√t)) ^(+∞) e^(−u^2 ) (du/(√t)) = (1/(√t)) e^(a^2 /(4t)) ( ∫_0 ^∞ e^(−u^2 ) du − ∫_0 ^(a/(√t)) e^(−u^2 ) du) = (1/(√t)) e^(a^2 /(4t)) ( ((√π)/2) − ∫_0 ^(a/(√t)) e^(−u^2 ) du) and by the same manner we get ∫_0 ^∞ e^(−tx^2 −bx) dx = (1/(√t)) e^(b^2 /(4t)) ( ((√π)/2) − ∫_0 ^(b/(√t)) e^(−u^2 ) du) f^′ (t)= ((√π_ )/(2(√t)))( e^(b^2 /(4t)) − e^(a^2 /(4t)) ) + ∫_0 ^(a/(√t)) e^(−u^2 ) du −∫_0 ^(b/(√t)) e^(−u^2 ) du = ((√π)/(2(√t))) ( e^(b^2 /(4t)) − e^(a^2 /(4t)) ) −∫_(a/(√t)) ^(b/(√t)) e^(−u^2 ) du = ψ(t) ⇒ f(t)= ∫_. ^t ψ(u)du +λ .](Q28135.png)
$$\left.{after}\:{verifying}\:{that}\:{f}\:{is}\:{derivable}\:{on}\:\right]\mathrm{0},+\infty\left[\:{we}\:{have}\:\right. \\ $$ $${f}^{,} \left({t}\right)=\:−\int_{\mathrm{0}} ^{\infty} \:\left(\:{e}^{−{ax}} \:−{e}^{−{bx}} \right){e}^{−{tx}^{\mathrm{2}} } {dx} \\ $$ $$=\int_{\mathrm{0}} ^{\infty} \:{e}^{−{tx}^{\mathrm{2}} −{bx}} {dx}\:−\int_{\mathrm{0}} ^{\infty} \:{e}^{−{tx}^{\mathrm{2}} −{ax}} {dx}\:\:\:{but} \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:{e}^{−{tx}^{\mathrm{2}} −{ax}} {dx}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left(\:\:\left(\sqrt{{t}}{x}\right)^{\mathrm{2}} \:+\mathrm{2}\frac{{a}}{\mathrm{2}\sqrt{{t}}}\left(\sqrt{{t}}{x}\right)\:+\:\frac{{a}^{\mathrm{2}} }{\mathrm{4}{t}}\:−\frac{{a}^{\mathrm{2}} }{\mathrm{4}{t}}\right)} {dx} \\ $$ $$=\:\:{e}^{\frac{{a}^{\mathrm{2}} }{\mathrm{4}{t}}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left(\sqrt{{t}}{x}\:+\frac{{a}}{\sqrt{{t}}}\right)^{\mathrm{2}} } {dx}\:\:\:\:\:{the}\:{ch}.\:\sqrt{{t}}{x}\:\:+\frac{{a}}{\sqrt{{t}}}={u}\:{give} \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{tx}^{\mathrm{2}} −{ax}} {dx}\:=\:{e}^{\frac{{a}^{\mathrm{2}} }{\mathrm{4}{t}}} \:\:\int_{\frac{{a}}{\sqrt{{t}}}} ^{+\infty} \:\:{e}^{−{u}^{\mathrm{2}} } \:\frac{{du}}{\sqrt{{t}}} \\ $$ $$=\:\frac{\mathrm{1}}{\sqrt{{t}}}\:{e}^{\frac{{a}^{\mathrm{2}} }{\mathrm{4}{t}}} \:\left(\:\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{u}^{\mathrm{2}} } {du}\:−\:\int_{\mathrm{0}} ^{\frac{{a}}{\sqrt{{t}}}} \:\:{e}^{−{u}^{\mathrm{2}} } {du}\right) \\ $$ $$=\:\frac{\mathrm{1}}{\sqrt{{t}}}\:{e}^{\frac{{a}^{\mathrm{2}} }{\mathrm{4}{t}}} \:\:\left(\:\:\:\:\frac{\sqrt{\pi}}{\mathrm{2}}\:\:−\:\int_{\mathrm{0}} ^{\frac{{a}}{\sqrt{{t}}}} \:\:{e}^{−{u}^{\mathrm{2}} } {du}\right)\:{and}\:{by}\:{the}\:{same}\:{manner} \\ $$ $${we}\:{get}\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{tx}^{\mathrm{2}} −{bx}} {dx}\:=\:\frac{\mathrm{1}}{\sqrt{{t}}}\:{e}^{\frac{{b}^{\mathrm{2}} }{\mathrm{4}{t}}} \left(\:\:\frac{\sqrt{\pi}}{\mathrm{2}}\:−\:\int_{\mathrm{0}} ^{\frac{{b}}{\sqrt{{t}}}} {e}^{−{u}^{\mathrm{2}} } {du}\right) \\ $$ $${f}^{'} \left({t}\right)=\:\frac{\sqrt{\pi_{} }}{\mathrm{2}\sqrt{{t}}}\left(\:\:{e}^{\frac{{b}^{\mathrm{2}} }{\mathrm{4}{t}}} \:−\:{e}^{\frac{{a}^{\mathrm{2}} }{\mathrm{4}{t}}} \right)\:+\:\int_{\mathrm{0}} ^{\frac{{a}}{\sqrt{{t}}}} \:\:{e}^{−{u}^{\mathrm{2}} } {du}\:\:−\int_{\mathrm{0}} ^{\frac{{b}}{\sqrt{{t}}}} \:\:{e}^{−{u}^{\mathrm{2}} } {du} \\ $$ $$=\:\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{{t}}}\:\left(\:\:{e}^{\frac{{b}^{\mathrm{2}} }{\mathrm{4}{t}}} \:\:−\:{e}^{\frac{{a}^{\mathrm{2}} }{\mathrm{4}{t}}} \right)\:−\int_{\frac{{a}}{\sqrt{{t}}}} ^{\frac{{b}}{\sqrt{{t}}}} \:\:{e}^{−{u}^{\mathrm{2}} } \:{du}\:=\:\:\psi\left({t}\right)\:\Rightarrow \\ $$ $${f}\left({t}\right)=\:\int_{.} ^{{t}} \:\psi\left({u}\right){du}\:\:+\lambda\:\:.\: \\ $$
