
Question Number 27699 by NECx last updated on 13/Jan/18
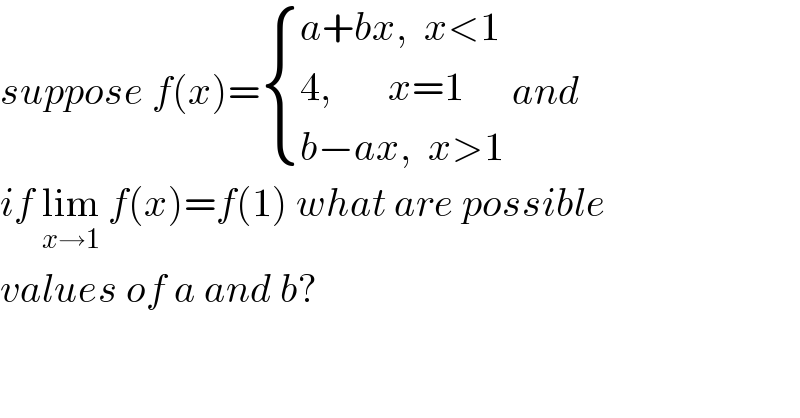
$${suppose}\:{f}\left({x}\right)=\begin{cases}{{a}+{bx},\:\:{x}<\mathrm{1}}\\{\mathrm{4},\:\:\:\:\:\:\:{x}=\mathrm{1}}\\{{b}−{ax},\:\:{x}>\mathrm{1}}\end{cases}\:{and} \\ $$ $${if}\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:{f}\left({x}\right)={f}\left(\mathrm{1}\right)\:{what}\:{are}\:{possible} \\ $$ $${values}\:{of}\:{a}\:{and}\:{b}? \\ $$ $$ \\ $$
Answered by peileng8802 last updated on 13/Jan/18
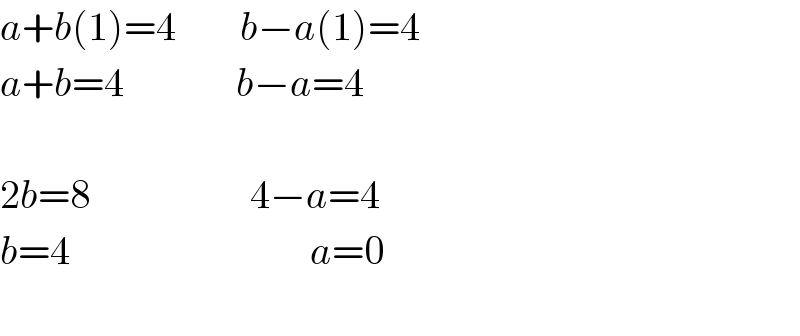
$${a}+{b}\left(\mathrm{1}\right)=\mathrm{4}\:\:\:\:\:\:\:\:{b}−{a}\left(\mathrm{1}\right)=\mathrm{4} \\ $$ $${a}+{b}=\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:\:\:{b}−{a}=\mathrm{4} \\ $$ $$ \\ $$ $$\mathrm{2}{b}=\mathrm{8}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}−{a}=\mathrm{4} \\ $$ $${b}=\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}=\mathrm{0} \\ $$ $$ \\ $$
Commented byNECx last updated on 13/Jan/18

$${thanks}\:{so}\:{much} \\ $$
