
Previous in Differential Equation Next in Differential Equation
Question Number 27696 by chernoaguero@gmail.com last updated on 12/Jan/18
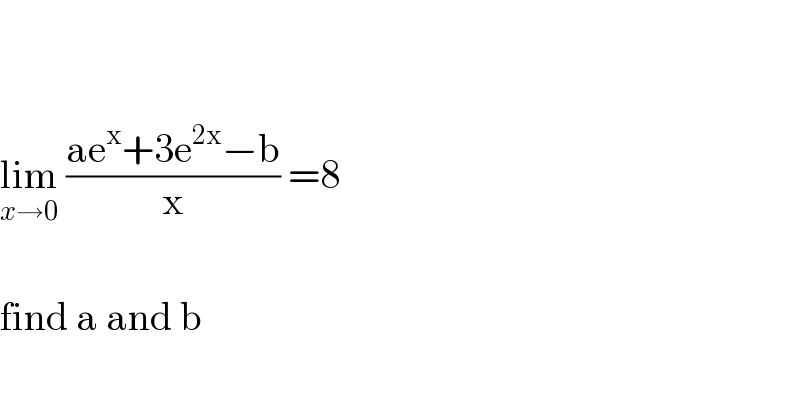
$$ \\ $$$$ \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ae}^{\mathrm{x}} +\mathrm{3e}^{\mathrm{2x}} −\mathrm{b}}{\mathrm{x}}\:=\mathrm{8} \\ $$$$ \\ $$$$\mathrm{find}\:\mathrm{a}\:\mathrm{and}\:\mathrm{b} \\ $$
Commented by abdo imad last updated on 12/Jan/18
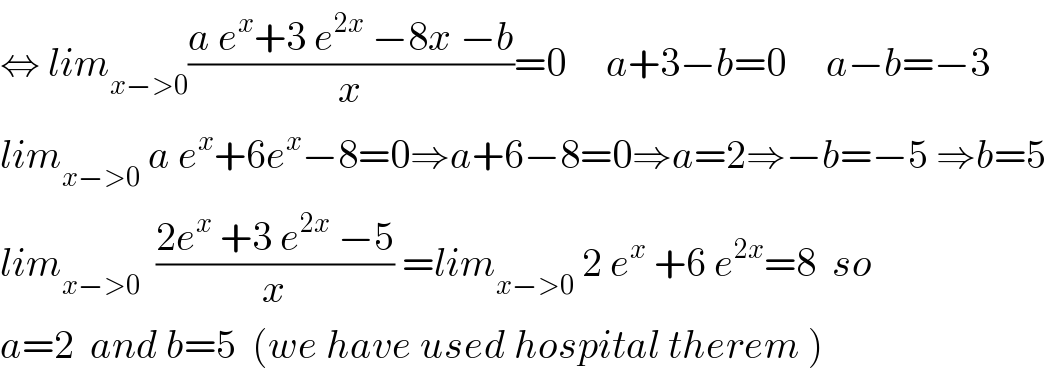
$$\Leftrightarrow\:{lim}_{{x}−>\mathrm{0}} \frac{{a}\:{e}^{{x}} +\mathrm{3}\:{e}^{\mathrm{2}{x}} \:−\mathrm{8}{x}\:−{b}}{{x}}=\mathrm{0}\:\:\:\:\:{a}+\mathrm{3}−{b}=\mathrm{0}\:\:\:\:\:{a}−{b}=−\mathrm{3} \\ $$$${lim}_{{x}−>\mathrm{0}} \:{a}\:{e}^{{x}} +\mathrm{6}{e}^{{x}} −\mathrm{8}=\mathrm{0}\Rightarrow{a}+\mathrm{6}−\mathrm{8}=\mathrm{0}\Rightarrow{a}=\mathrm{2}\Rightarrow−{b}=−\mathrm{5}\:\Rightarrow{b}=\mathrm{5} \\ $$$${lim}_{{x}−>\mathrm{0}} \:\:\frac{\mathrm{2}{e}^{{x}} \:+\mathrm{3}\:{e}^{\mathrm{2}{x}} \:−\mathrm{5}}{{x}}\:={lim}_{{x}−>\mathrm{0}} \:\mathrm{2}\:{e}^{{x}} \:+\mathrm{6}\:{e}^{\mathrm{2}{x}} =\mathrm{8}\:\:{so} \\ $$$${a}=\mathrm{2}\:\:{and}\:{b}=\mathrm{5}\:\:\left({we}\:{have}\:{used}\:{hospital}\:{therem}\:\right) \\ $$
Commented by chernoaguero@gmail.com last updated on 12/Jan/18

$$\mathrm{ok}\:\mathrm{thank}\:\mathrm{u}\:\mathrm{sir}\: \\ $$
