
Question Number 27400 by Tinkutara last updated on 06/Jan/18
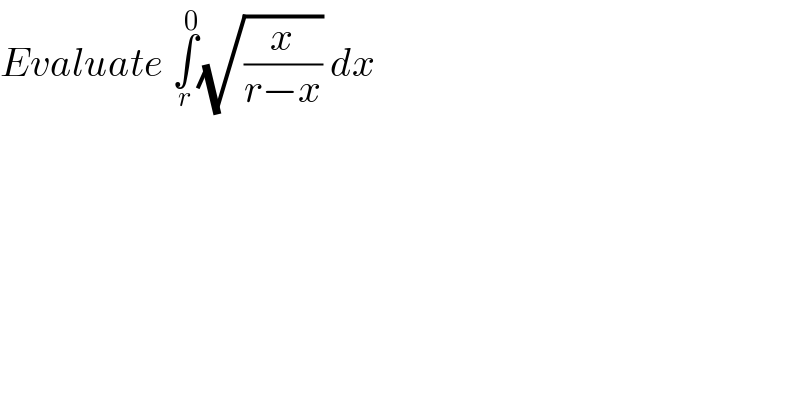
$${Evaluate}\:\underset{{r}} {\overset{\mathrm{0}} {\int}}\sqrt{\frac{{x}}{{r}−{x}}}\:{dx} \\ $$
Commented by Tinkutara last updated on 07/Jan/18

$${But}\:{this}\:{integral}\:{was}\:{used}\:{in}\:{a}\:{Physics} \\ $$$${question}\:{where}\:{its}\:{value}\:{can}'{t}\:{be} \\ $$$${negative}.\:{It}\:{should}\:{be}\:{only}\:\frac{\pi{r}}{\mathrm{2}}.\:{It}\:{is} \\ $$$${used}\:{in}\:{question}\:\mathrm{27445}. \\ $$
Commented by abdo imad last updated on 06/Jan/18

$${let}\:{do}\:{the}\:{ch}.\:\:\:\sqrt{\frac{{x}}{{r}−{x}}}\:\:\:={t}\Leftrightarrow\:\:\frac{{x}}{{r}−{x}}\:={t}^{\mathrm{2}} \Leftrightarrow{x}=\left({r}−{x}\right){t}^{\mathrm{2}} \\ $$$$\Leftrightarrow{x}+{xt}^{\mathrm{2}} ={rt}^{\mathrm{2}} \Leftrightarrow\:\left(\mathrm{1}+{t}^{\mathrm{2}} \right){x}={rt}^{\mathrm{2}} \Leftrightarrow{x}=\:\frac{{rt}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:\: \\ $$$${x}=\frac{{r}\left(\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }\:={r}\:−\frac{{r}}{\mathrm{1}+{t}^{\mathrm{2}} }\Leftrightarrow\:\frac{{dx}}{{dt}}=\:\frac{\mathrm{2}{rt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\int_{{r}} ^{\mathrm{0}} \sqrt{\frac{{x}}{{r}−{x}}}\:{dx}=\:\int_{\propto} ^{\mathrm{0}} {t}\frac{\mathrm{2}{rt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}\:=\:−\mathrm{2}{r}\:\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt} \\ $$$${but}\:\:\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}=\:\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:−\int_{\mathrm{0}} ^{\infty} \:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\pi}{\mathrm{2}}\:−\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{and}\:{by}\:{residus}\:{theorem} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\int_{{R}} \:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{2}{i}\pi\:{Res}\left({f}\:,{i}\right){with} \\ $$$${f}\left({z}\right)=\:\frac{\mathrm{1}}{\left(\mathrm{1}+{z}^{\mathrm{2}} \right)^{\mathrm{2}} }=\:\frac{\mathrm{1}}{\left({z}−{i}\right)^{\mathrm{2}} \left({z}+{i}\right)^{\mathrm{2}} }\:{and}\:{i}\:{is}\:{a}\:{double}\:{pole}\:{of}\:{f} \\ $$$${Res}\left({f},{i}\right)={lim}_{{z}−>{i}} \:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left(\left({z}−{i}\right)^{\mathrm{2}} {f}\left({z}\right)\right)^{,} \\ $$$$={lim}_{{z}−>{i}} \left(\left({z}+{i}\right)^{−\mathrm{2}} \right)^{,} ={lim}_{{z}−>{i}} −\mathrm{2}\left({z}+{i}\right)^{−\mathrm{3}} \\ $$$$=\:−\mathrm{2}\left(\mathrm{2}{i}\right)^{−\mathrm{3}} =−\mathrm{2}\frac{\mathrm{1}}{\left(\mathrm{2}{i}\right)^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{4}{i}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }={i}\pi\:\frac{\mathrm{1}}{\mathrm{4}{i}}=\:\frac{\pi}{\mathrm{4}} \\ $$$$\int_{{r}} ^{\mathrm{0}} \sqrt{\:\:\frac{{x}}{{r}−{x}}}\:{dx}\:=−\mathrm{2}{r}\left(\frac{\pi}{\mathrm{2}}\:−\frac{\pi}{\mathrm{4}}\right)=−\mathrm{2}{r}\:\frac{\pi}{\mathrm{4}}\:=\frac{−{r}\pi}{\mathrm{2}}\:. \\ $$
Commented by mrW1 last updated on 07/Jan/18

$${the}\:{result}\:{above}\:{is}\:{correct}. \\ $$$$ \\ $$$$\int_{{r}} ^{\:\mathrm{0}} \sqrt{...}\:{dx}\:{is}\:{negative} \\ $$$$\int_{\mathrm{0}} ^{\:{r}} \sqrt{...}\:{dx}\:{is}\:{positive} \\ $$
Commented by abdo imad last updated on 07/Jan/18
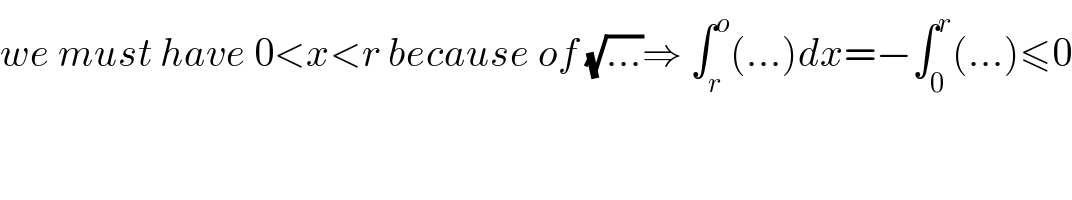
$${we}\:{must}\:{have}\:\mathrm{0}<{x}<{r}\:{because}\:{of}\:\sqrt{...}\Rightarrow\:\int_{{r}} ^{{o}} \left(...\right){dx}=−\int_{\mathrm{0}} ^{{r}} \left(...\right)\leqslant\mathrm{0} \\ $$
Answered by prakash jain last updated on 07/Jan/18
![x=rcos^2 θ dx=−2rcos θsin θdθ ∫−2rcos θsin θ.((cos θ)/(sin θ))dθ =−r∫2cos^2 θdθ =−r∫(1+cos 2θ)dθ =−r[θ+((sin 2θ)/2)]+C =−r[cos^(−1) (√(x/r))+(√((x/r)×((r−x)/r)))]+C =−r[cos^(−1) (√(x/r))+(1/r)(√(x(r−x)))]+C taking limits =−r[(π/2)−0]=−((πr)/2)](Q27476.png)
$${x}={r}\mathrm{cos}^{\mathrm{2}} \:\theta \\ $$$${dx}=−\mathrm{2}{r}\mathrm{cos}\:\theta\mathrm{sin}\:\theta{d}\theta \\ $$$$\int−\mathrm{2}{r}\mathrm{cos}\:\theta\mathrm{sin}\:\theta.\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}{d}\theta \\ $$$$=−{r}\int\mathrm{2cos}^{\mathrm{2}} \theta{d}\theta \\ $$$$=−{r}\int\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta\right){d}\theta \\ $$$$=−{r}\left[\theta+\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}}\right]+{C} \\ $$$$=−{r}\left[\mathrm{cos}^{−\mathrm{1}} \sqrt{\frac{{x}}{{r}}}+\sqrt{\frac{{x}}{{r}}×\frac{{r}−{x}}{{r}}}\right]+{C} \\ $$$$=−{r}\left[\mathrm{cos}^{−\mathrm{1}} \sqrt{\frac{{x}}{{r}}}+\frac{\mathrm{1}}{{r}}\sqrt{{x}\left({r}−{x}\right)}\right]+{C} \\ $$$${taking}\:{limits} \\ $$$$=−{r}\left[\frac{\pi}{\mathrm{2}}−\mathrm{0}\right]=−\frac{\pi{r}}{\mathrm{2}} \\ $$
Commented by mrW1 last updated on 07/Jan/18

$${very}\:{nice}\:{way}! \\ $$
