
Question Number 162003 by mathlove last updated on 25/Dec/21
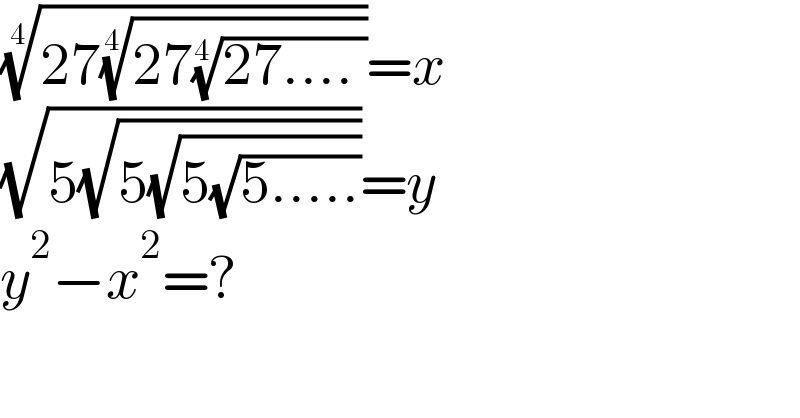
$$\sqrt[{\mathrm{4}}]{\mathrm{27}\sqrt[{\mathrm{4}}]{\mathrm{27}\sqrt[{\mathrm{4}}]{\mathrm{27}....\:}}}={x} \\ $$$$\sqrt{\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}.....}}}}={y} \\ $$$${y}^{\mathrm{2}} −{x}^{\mathrm{2}} =? \\ $$
Answered by Rasheed.Sindhi last updated on 25/Dec/21
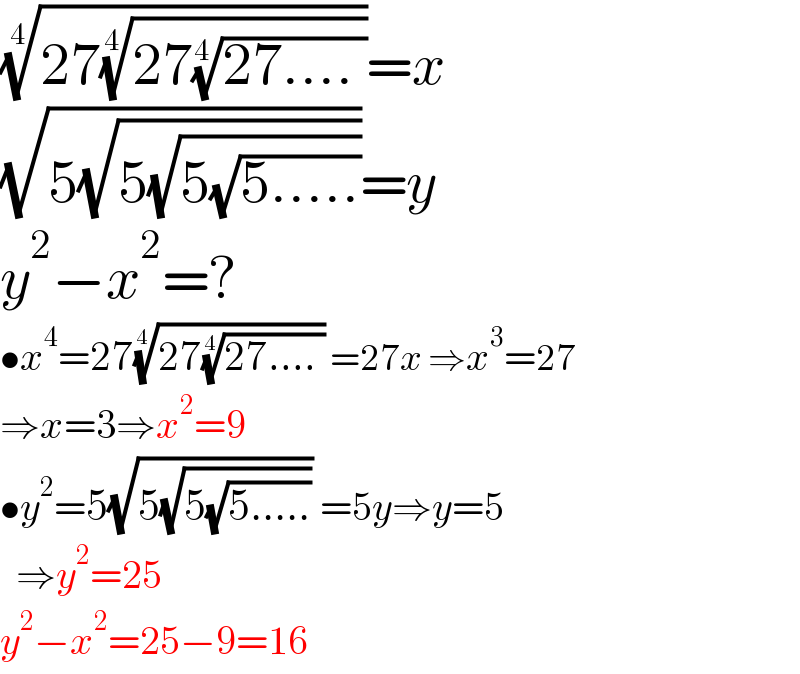
$$\sqrt[{\mathrm{4}}]{\mathrm{27}\sqrt[{\mathrm{4}}]{\mathrm{27}\sqrt[{\mathrm{4}}]{\mathrm{27}....\:}}}={x} \\ $$$$\sqrt{\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}.....}}}}={y} \\ $$$${y}^{\mathrm{2}} −{x}^{\mathrm{2}} =? \\ $$$$\bullet{x}^{\mathrm{4}} =\mathrm{27}\sqrt[{\mathrm{4}}]{\mathrm{27}\sqrt[{\mathrm{4}}]{\mathrm{27}....\:}}\:=\mathrm{27}{x}\:\Rightarrow{x}^{\mathrm{3}} =\mathrm{27} \\ $$$$\Rightarrow{x}=\mathrm{3}\Rightarrow{x}^{\mathrm{2}} =\mathrm{9} \\ $$$$\bullet{y}^{\mathrm{2}} =\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}.....}}}\:=\mathrm{5}{y}\Rightarrow{y}=\mathrm{5} \\ $$$$\:\:\Rightarrow{y}^{\mathrm{2}} =\mathrm{25} \\ $$$${y}^{\mathrm{2}} −{x}^{\mathrm{2}} =\mathrm{25}−\mathrm{9}=\mathrm{16} \\ $$
Answered by aleks041103 last updated on 25/Dec/21
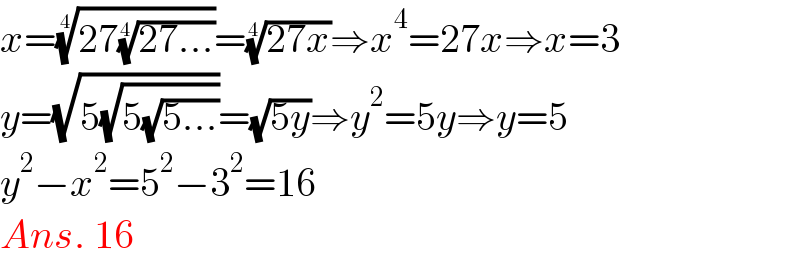
$${x}=\sqrt[{\mathrm{4}}]{\mathrm{27}\sqrt[{\mathrm{4}}]{\mathrm{27}...}}=\sqrt[{\mathrm{4}}]{\mathrm{27}{x}}\Rightarrow{x}^{\mathrm{4}} =\mathrm{27}{x}\Rightarrow{x}=\mathrm{3} \\ $$$${y}=\sqrt{\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}...}}}=\sqrt{\mathrm{5}{y}}\Rightarrow{y}^{\mathrm{2}} =\mathrm{5}{y}\Rightarrow{y}=\mathrm{5} \\ $$$${y}^{\mathrm{2}} −{x}^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} =\mathrm{16} \\ $$$${Ans}.\:\mathrm{16} \\ $$
