
Question Number 25845 by NECx last updated on 15/Dec/17

$${using}\:{the}\:\mathrm{1}{st}\:{principle}\:{find}\:{the} \\ $$$${derivative}\:{of}\: \\ $$$$\:\:\:\:\:{y}=\left({ax}+{b}\right)^{{n}} \\ $$
Answered by ajfour last updated on 15/Dec/17
![(dy/dx)=lim_(h→0) (((ax+ah+b)^n −(ax+b)^n )/h) =lim_(h→0) ((ah)/h)×lim_(h→0) [(ax+ah+b)^(n−1) + (ax+ah+b)^(n−2) (ax+b)+ (ax+ah+b)^(n−3) (ax+b)^2 +... .....+ (ax+ah+b)(ax+b)^(n−2) + (ax+b)^(n−1) ] ((d(ax+b)^n )/dx)=an(ax+b)^(n−1) .](Q25857.png)
$$\frac{{dy}}{{dx}}=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({ax}+{ah}+{b}\right)^{{n}} −\left({ax}+{b}\right)^{{n}} }{{h}} \\ $$$$\:\:\:\:=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{ah}}{{h}}×\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left({ax}+{ah}+{b}\right)^{{n}−\mathrm{1}} +\right. \\ $$$$\:\:\:\:\:\:\left({ax}+{ah}+{b}\right)^{{n}−\mathrm{2}} \left({ax}+{b}\right)+ \\ $$$$\:\:\:\:\:\:\left({ax}+{ah}+{b}\right)^{{n}−\mathrm{3}} \left({ax}+{b}\right)^{\mathrm{2}} +... \\ $$$$\:\:\:.....+\:\left({ax}+{ah}+{b}\right)\left({ax}+{b}\right)^{{n}−\mathrm{2}} + \\ $$$$\left.\:\:\:\:\:\:\:\left({ax}+{b}\right)^{{n}−\mathrm{1}} \right] \\ $$$$\:\:\:\:\frac{{d}\left({ax}+{b}\right)^{{n}} }{{dx}}={an}\left({ax}+{b}\right)^{{n}−\mathrm{1}} \:. \\ $$
Commented by NECx last updated on 16/Dec/17
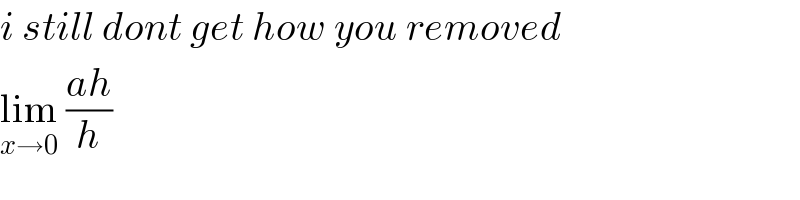
$${i}\:{still}\:{dont}\:{get}\:{how}\:{you}\:{removed} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ah}}{{h}} \\ $$
Commented by ajfour last updated on 16/Dec/17
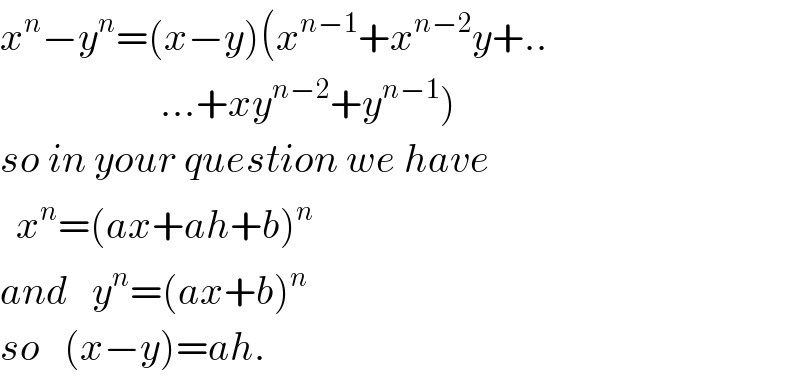
$${x}^{{n}} −{y}^{{n}} =\left({x}−{y}\right)\left({x}^{{n}−\mathrm{1}} +{x}^{{n}−\mathrm{2}} {y}+..\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...+{xy}^{{n}−\mathrm{2}} +{y}^{{n}−\mathrm{1}} \right) \\ $$$${so}\:{in}\:{your}\:{question}\:{we}\:{have} \\ $$$$\:\:{x}^{{n}} =\left({ax}+{ah}+{b}\right)^{{n}} \\ $$$${and}\:\:\:{y}^{{n}} =\left({ax}+{b}\right)^{{n}} \\ $$$${so}\:\:\:\left({x}−{y}\right)={ah}. \\ $$
Answered by rita1608 last updated on 15/Dec/17
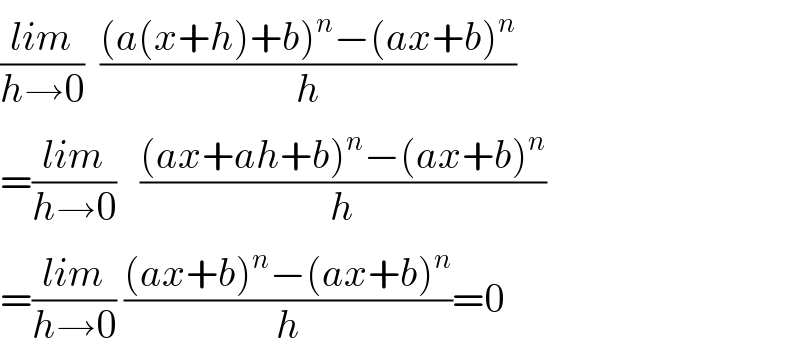
$$\frac{{lim}}{{h}\rightarrow\mathrm{0}}\:\:\frac{\left({a}\left({x}+{h}\right)+{b}\right)^{{n}} −\left({ax}+{b}\right)^{{n}} }{{h}} \\ $$$$=\frac{{lim}}{{h}\rightarrow\mathrm{0}}\:\:\:\frac{\left({ax}+{ah}+{b}\right)^{{n}} −\left({ax}+{b}\right)^{{n}} }{{h}} \\ $$$$=\frac{{lim}}{{h}\rightarrow\mathrm{0}}\:\frac{\left({ax}+{b}\right)^{{n}} −\left({ax}+{b}\right)^{{n}} }{{h}}=\mathrm{0} \\ $$
Commented by rita1608 last updated on 16/Dec/17
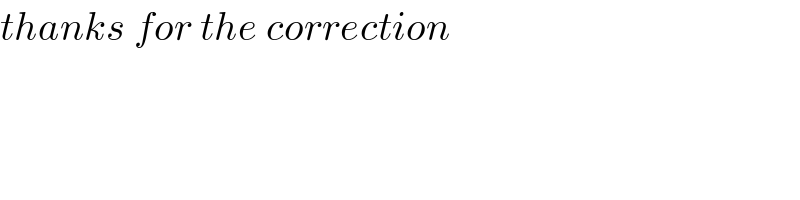
$${thanks}\:{for}\:{the}\:{correction}\: \\ $$$$ \\ $$
Commented by prakash jain last updated on 15/Dec/17

$$\mathrm{In}\:\mathrm{the}\:\mathrm{last}\:\mathrm{step}\:\mathrm{you}\:\mathrm{substituted} \\ $$$${h}=\mathrm{0}\:\mathrm{in}\:\mathrm{numerator}\:\mathrm{and}\:\mathrm{left} \\ $$$${h}\:\mathrm{in}\:\mathrm{denominator}.\:\mathrm{This}\:\mathrm{is}\:\mathrm{not}\:\mathrm{correct}. \\ $$$$\mathrm{with}\:\mathrm{this}\:\mathrm{you}\:\mathrm{will}\:\mathrm{get}\:\mathrm{0}\:\mathrm{for}\:\mathrm{every} \\ $$$$\mathrm{derivative}. \\ $$
