
Question Number 25569 by rita1608 last updated on 11/Dec/17
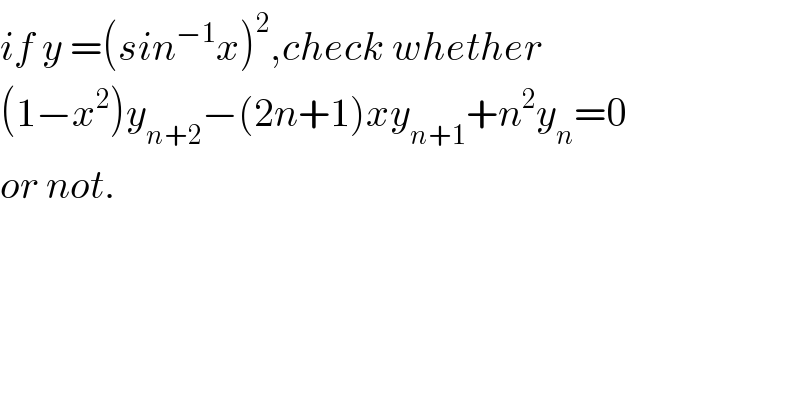
$${if}\:{y}\:=\left({sin}^{−\mathrm{1}} {x}\right)^{\mathrm{2}} ,{check}\:{whether} \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y}_{{n}+\mathrm{2}} −\left(\mathrm{2}{n}+\mathrm{1}\right){xy}_{{n}+\mathrm{1}} +{n}^{\mathrm{2}} {y}_{{n}} =\mathrm{0} \\ $$$${or}\:{not}. \\ $$
Commented by prakash jain last updated on 12/Dec/17
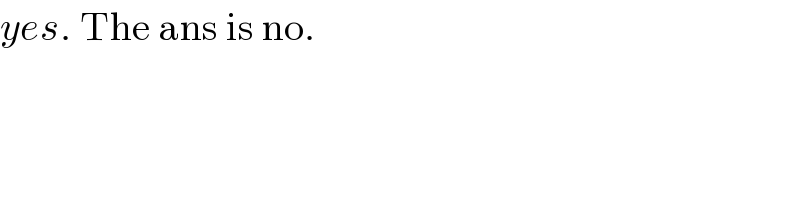
$${yes}.\:\mathrm{The}\:\mathrm{ans}\:\mathrm{is}\:\mathrm{no}. \\ $$
Commented by rita1608 last updated on 11/Dec/17
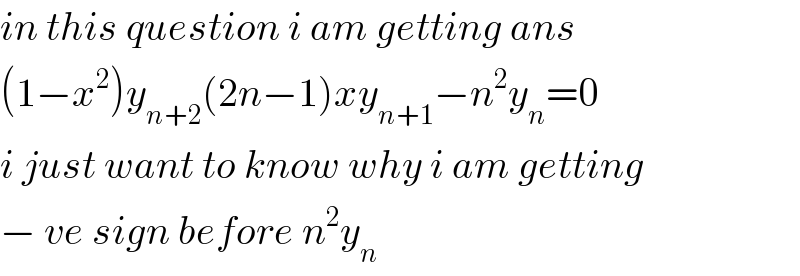
$${in}\:{this}\:{question}\:{i}\:{am}\:{getting}\:{ans}\: \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y}_{{n}+\mathrm{2}} \left(\mathrm{2}{n}−\mathrm{1}\right){xy}_{{n}+\mathrm{1}} −{n}^{\mathrm{2}} {y}_{{n}} =\mathrm{0} \\ $$$${i}\:{just}\:{want}\:{to}\:{know}\:{why}\:{i}\:{am}\:{getting}\: \\ $$$$−\:{ve}\:{sign}\:{before}\:{n}^{\mathrm{2}} {y}_{{n}\:} \\ $$
Commented by prakash jain last updated on 11/Dec/17

$$\mathrm{Can}\:\mathrm{u}\:\mathrm{please}\:\mathrm{share}\:\mathrm{your}\:\mathrm{workings}? \\ $$
Commented by rita1608 last updated on 12/Dec/17

$${ok}\: \\ $$
Commented by prakash jain last updated on 12/Dec/17
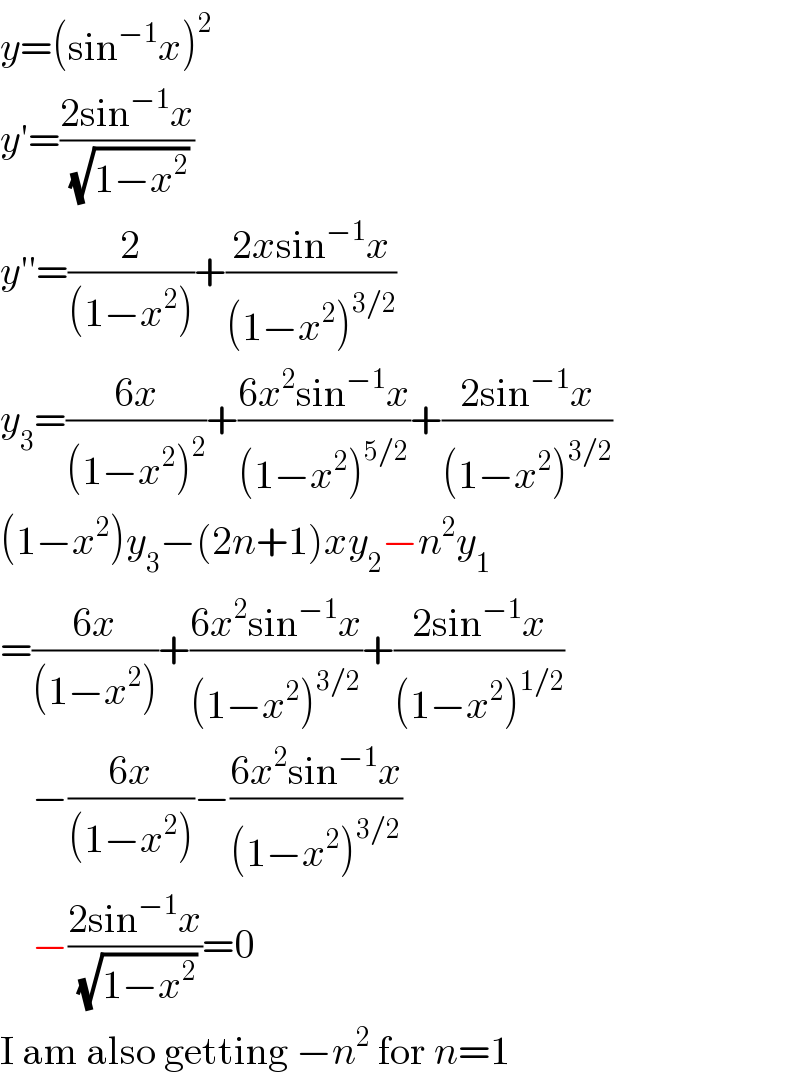
$${y}=\left(\mathrm{sin}^{−\mathrm{1}} {x}\right)^{\mathrm{2}} \\ $$$${y}'=\frac{\mathrm{2sin}^{−\mathrm{1}} {x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${y}''=\frac{\mathrm{2}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}+\frac{\mathrm{2}{x}\mathrm{sin}^{−\mathrm{1}} {x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} } \\ $$$${y}_{\mathrm{3}} =\frac{\mathrm{6}{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }+\frac{\mathrm{6}{x}^{\mathrm{2}} \mathrm{sin}^{−\mathrm{1}} {x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}/\mathrm{2}} }+\frac{\mathrm{2sin}^{−\mathrm{1}} {x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} } \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y}_{\mathrm{3}} −\left(\mathrm{2}{n}+\mathrm{1}\right){xy}_{\mathrm{2}} −{n}^{\mathrm{2}} {y}_{\mathrm{1}} \\ $$$$=\frac{\mathrm{6}{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}+\frac{\mathrm{6}{x}^{\mathrm{2}} \mathrm{sin}^{−\mathrm{1}} {x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }+\frac{\mathrm{2sin}^{−\mathrm{1}} {x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{1}/\mathrm{2}} } \\ $$$$\:\:\:\:−\frac{\mathrm{6}{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}−\frac{\mathrm{6}{x}^{\mathrm{2}} \mathrm{sin}^{−\mathrm{1}} {x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} } \\ $$$$\:\:\:\:−\frac{\mathrm{2sin}^{−\mathrm{1}} {x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}=\mathrm{0} \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{also}\:\mathrm{getting}\:−{n}^{\mathrm{2}} \:\mathrm{for}\:{n}=\mathrm{1} \\ $$
Commented by rita1608 last updated on 12/Dec/17
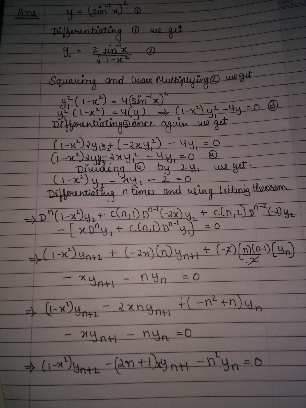
Commented by prakash jain last updated on 12/Dec/17
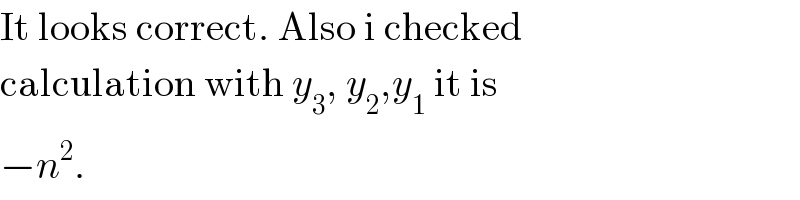
$$\mathrm{It}\:\mathrm{looks}\:\mathrm{correct}.\:\mathrm{Also}\:\mathrm{i}\:\mathrm{checked} \\ $$$$\mathrm{calculation}\:\mathrm{with}\:{y}_{\mathrm{3}} ,\:{y}_{\mathrm{2}} ,{y}_{\mathrm{1}} \:\mathrm{it}\:\mathrm{is} \\ $$$$−{n}^{\mathrm{2}} . \\ $$
Commented by rita1608 last updated on 12/Dec/17
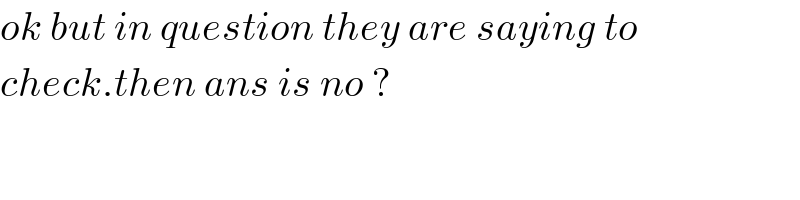
$${ok}\:{but}\:{in}\:{question}\:{they}\:{are}\:{saying}\:{to}\: \\ $$$${check}.{then}\:{ans}\:{is}\:{no}\:? \\ $$
